说在开头：关于薛定谔的波动方程（3）

波动方程在矩阵派的内部也大受欢迎，首先是海森堡的老师索末菲，然后是建立矩阵力学的核心人物之一的另一位老师：马克思.玻恩。玻恩在薛定谔方程刚出来时就赞扬了他的成就，称波动方程是量子规律中最深刻的形式，这伤透了海森堡的心。但玻恩对薛定谔方程的赞赏并不表示他和薛定谔是站在一个战壕里的，因为对于同一个方程用不同的角度去解释，它却是天差地别（关乎不同科学家之间的哲学理念之争）；那么最重要的一个问题是：薛定谔的那个波函数Ψ，其物理意义到底是什么呢？

薛定谔说：“波函数Ψ是一个空间分布函数，当它和电子的电荷相乘，就代表了电荷在空间中的实际分布；电子不是一个粒子而是一个波，像云彩一样在空间中四周扩展开去，我们的波函数恰恰描述了这种扩展和它的行为，电子是没有具体位置的，它也没有具体的路径，因为它是一团云，是一个波，它向每一个方向延伸——虽然衰减的很快，这使它看起来像一个粒子。当把电子拉出来放大，你会发现它们在空间里融化开来，变成无数振动的叠加。是的，一个电子就像涂在面包上的黄油那样，它平时卷缩得那么紧，以至于我们把它当成了小球。”

薛定谔的讲解获得了大部分人的掌声和喝彩声，但是有一个人在摇头，显得不以为然的样子；薛定谔认出来是哥廷根的玻恩，咦，这老小子不是刚刚赞赏过我的方程嘛？玻恩清了清嗓子，脸上泛起神秘的微笑：我觉得这波函数就是一个骰子。

骰子是什么？在物理学来说，它代表了不确定。但物理学不是一门严格、精密、不容不确定的科学吗？当1926年7月玻恩将骰子带进了物理学后，这引起了何等的轩然大波。这将引起20世纪物理史学上最著名的一场论战。而玻恩要一直等到28年后，才因为这一杰出的发现而获得诺贝尔物理学奖。骰子才是薛定谔波函数φ的正确解释：它代表了一种随机和概率，而不是电子电荷在空间中的实际分布。玻恩说：“φ的平方，代表了电子在某个地点出现的概率。电子本身不会像波那样扩展开去，但是它的出现概率则像一个波，严格的按照波函数φ的分布所展开。”

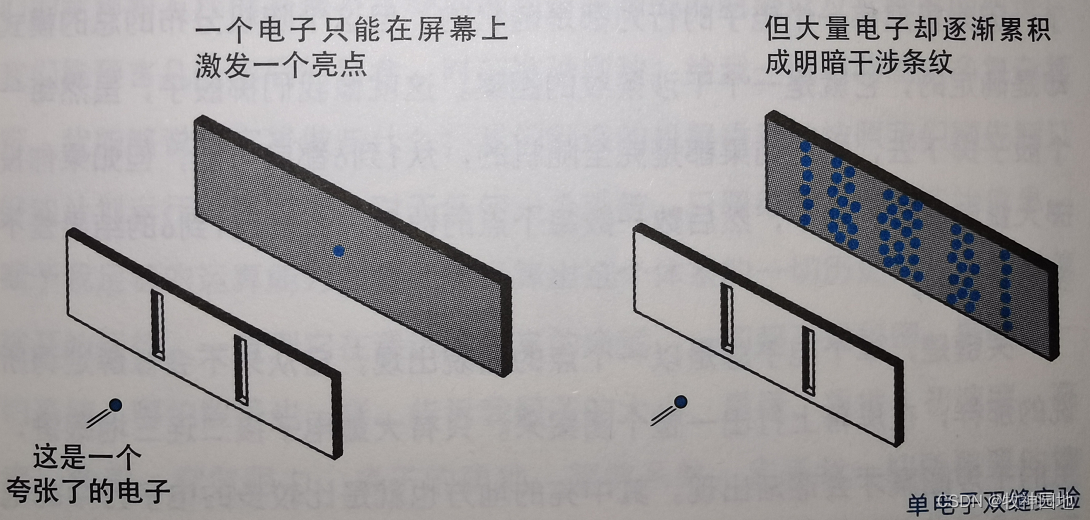
如上图电子双缝干涉实验，当电子穿过两道狭缝后，便在感应屏上组成了一个明暗相间的图案，展示了波峰和波谷的相互增强和抵消，但是正如粒子派所指出的那样，每次电子只会在屏上打出一个小点，只有成群的电子穿过双缝后，才会组成整个图案。我们大量观察单个电子，它并非是没有规律的：电子在某些地方出现的可能性大一些，在另一些地方小一些。它出现频率高的地方，恰恰是波动所预言的干涉条纹的亮处，它出现频率低的地方则对应于暗处。我们现在可以理解了：因为虽然每一个电子的行为是随机的，但这个随机分布的总的模式却是确定的，即，一个干涉条纹的图案。就像是掷骰子：每次结果是1~6都有可能，但最后统计结果1~6的次数是差不多的。所以，我们能预言的只是概率而已。

这事不得了了，千百年以来成千上万的先辈为这门科学呕心沥血，物理学的力量统治整个宇宙，从星系到原子，万事万物都在它的统治下有序的运转着。物理学不仅能够解释过去和现在，还能预言未来。事实上对于任何一个系统，只要给定足够多的初始信息，给于足够的运算能力，我就能够推算出这个系统的一切历史，以及遥远未来的命运。哪怕是骰子，如果知道骰子的质量、初速度、高度、角度、空气阻力，摩擦力等等所有需要的信息，还有足够的运算能力，那么我就可以毫不迟疑的预言这个骰子将掷出几点来。这是历史上所有物理学家的信仰：宇宙从它出生的那一刻开始，就坠入一个预定的轨道，它严格的按照物理定律发展，没有任何岔路可走，一直到它命运的终点（决定论）。但现在有人说，物理不能预测电子的行为，它只能找到电子出现的概率而已；玻恩解释说：就算我们把电子的初始状态测量的精确无比，就算我们拥有最强大的计算机可以计算一切环境对电子的影响，我们也不能预言电子最后的准确位置；这种不确定，不是因为我们计算能力的不足，而是物理定律本身内部的一种属性。

20世纪最著名的争论即将展开，其影响一直延续至今。（参考自：曹天元-上帝掷骰子吗）

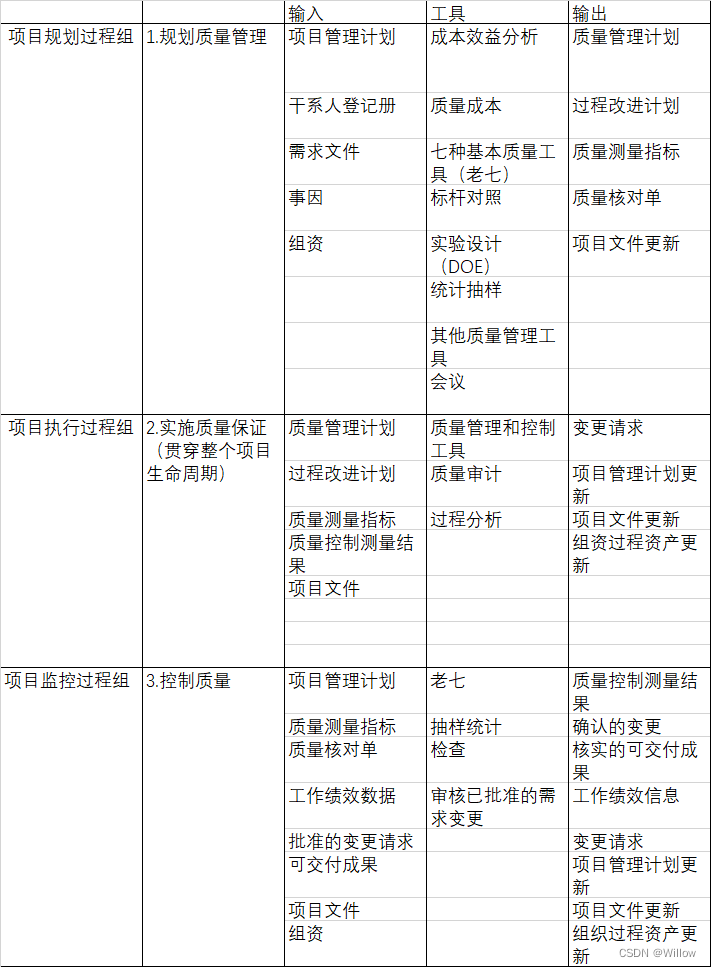
二，半桥和全桥变换器拓扑

半桥和全桥拓扑开关管的稳态关断电压等于直流输入电压Vdc（类似于双端正激变拓扑），而不像推挽、单端正激式和交错正激式拓扑是输入电压Vdc的2倍。所以桥式拓扑广泛应用于直接电网的离线隔离式变压器，而对于推挽式等拓扑来说，当输入电压达到220V或更高时将超过开关管的耐压容限。所以一般大功率（几百W以上）输入级开关电源拓扑，目前大多采用桥式拓扑。其另外一个优点是：能将变压器漏感尖峰电压钳位在输入电源母线上，并将漏感存储的能量归还到母线，而不是损耗在阻性元件中。

1，半桥拓扑原理

1.1半桥拓扑结构和特点

半桥拓扑结构如下图所示，其特点为：

1. 开关管时承受电压为Vdc，与双端正激拓扑相同（推挽或单端正激拓扑为2*Vdc）；

2. 半桥拓扑两个开关管轮流交替工作，相当于两个开关电源同时输出功率，约等于单一开关电源输出功率的一倍（双端正激拓扑的一倍），输出功率大；

3. 变压器原边线圈只需要一个绕组，对于小功率开关电源变压器绕制更加方便；

4. 两个开关器件：Q1和Q2没有公共地，开关管的驱动信号连接比较麻烦。

——如下图所示，Q2的S极连接GND，所以Q2的Vgs驱动电压为相对GND的电压；Q1的S极连接变压器，导通后电压为Vdc，那么Q2的Vgs驱动电压为相对Vdc的电压。

半桥拓扑电源的Q1和Q2均串接于变压器原边的顶端，结构分析如下：

1. 忽略Cb，则Np异名端可看作连接到C1和C2交接点；且若C1和C2相等，那么连接处电压近似为输入电压的1/2（Vdc2），可以在C1/C2两端各并等值电阻R1/R2来均衡两者的电压；

——变压器T1原边绕组线圈正向导通时的两端电压为：Vdc-Vdc/2 = Vdc/2，变压器反向导通时原边绕组线圈两端电压为：0-Vdc/2= -Vdc/2。

2. 开关管Q1和Q2轮流导通半个周期，避免Q1和Q2同时导通，需要增加Q1和Q2的死区时间；

——Q1和Q2同时导通，那么会导致Vdc通过Q1和Q2直接短路到GND，那么将导致开关管Q1和Q2过流损坏，设置导通时间Ton为80%的半周期。

3. Q1导通而Q2关断时：变压器原边Np绕组同名端电压为Vdc，所以Q2承受的最大电压为Vdc（(Vdc-Vds)-0 = Vdc-Vds ≈ Vdc）；同理Q1关断时：变压器原边Np绕组同名端电压为0V，所以Q1承受的最大电压为Vdc（Vdc-(0-Vds) = Vdc+Vds ≈ Vdc）。

在开关管导通和关断时不同节点电压/电流如上右图所示，半桥拓扑Q1/Q2工作过程如下：

1. Q1导通而Q2关断时：

1, Np同名端电压为Vdc，异名端电压为Vdc/2，变压器原边绕组Np两端电压为：Vdc/2，C2与Cb串联接至GND，电流通过C2回流到GND；

2, 变压器原边Np以及幅边Ns1和Ns2的同名端相对于异名端为正，整流二极管D1正向偏置，电流从Ns1同名端通过D1和L1输入C1滤波电容器和负载；

2. Q1关断时：

1, Np同名端电压为0V，异名端电压为Vdc/2，变压器原边绕组Np两端电压为： -Vdc/2，C1与Cb串联接至Vdc，电流通过C1回流到Vdc；

2, 由于变压器T1原边绕组Np被施加了反向电压（-Vdc/2），此时所有绕组原/副边的同名端相对异名端为负，整流二极管D2正向偏置，电流从同名端通过D2和L1输入C1滤波电容器和负载；

我们从半桥拓扑的特点看到，与双端正激变拓扑的特性非常相似，两者区别主要在于：

1. 半桥拓扑输出全波（类似推挽式拓扑）而双端正激变拓扑输出半波，半桥拓扑方波频率是双端正激变的2倍，所以半桥拓扑输出电感L和电容C可以更小；

2. 双端正激变拓扑占空比（Ton/T）只有半桥拓扑的一半，所以其次级峰值电压比半桥拓扑要高；

3. 双端正激变变压器需承受Vdc电压，半桥拓扑只需承受Vdc/2电压，所以变压器原边绕组数是半桥拓扑的一倍，半桥拓扑变压器成本更低、寄生电容更小；

4. 因为半桥拓扑相比于双端正激拓扑变压器绕组数更少，而邻近效应与绕组数量成正相关，由此导致的损耗更低。

1.2半桥拓扑设计关注点

1. 导通时间设计：

1, 如上所述，若Q1和Q2同时导通会使电源地瞬间短路而损坏开关管；为防止此现象发生，在最小输入Vdc时，Q1和Q2最大导通时间限制在半周期的80%（即0.4T）。

2. 原边绕组Np电流：

2, 假设效率为80%，则Pin=1.25*Po；电源输入电压最小Vdc时，Pin=Vdc*I²in，由于半周期导通时间为0.4T；Pin=1.25*Po=Vdc*Ipft*0.4T/T => Ipft=3.13Po/Vdc；

3, 在输出功率相同的条件下，半桥拓扑线径比推挽拓扑要大很多，但推挽电路有两个原边线圈，且承受的电压是半桥拓扑的2倍，所以整体体积相差不大。

3. 半桥拓扑的漏感问题：

1, 不存在类似单端正激和推挽拓扑中的漏感问题，当开关关断时通过并联的二极管D5/D6将漏感尖峰电压钳位在Vdc。

4. 阻断电容Cb选择：

1, 变压器原边串联电容Cb是为了防止推挽拓扑中的磁通不平衡问题，如下图所示，而磁通不平衡问题主要是原边置位伏秒数与复位伏秒数不相等导致的；

2, 若C1和C2接点处电压不能精确到电源电压的一半，那么Q1导通时初级绕阻承受电压与Q2导通时不相等；磁通会沿磁滞回线正向或反向持续增加直至磁心饱和，损坏开关管。

我们看到半桥拓扑的原边回流电路中有电容C1/C2/Cb隔离，所以其变压器原边电流必然是交流形式出现；电容器C1/C2/Cb一直在充放电循环状态，我一开始对此处有很大的疑惑：正如我《电感特性原理》章节所说，那时我认为能量传输的方向取决于电流的方向，而半桥拓扑的电流方向来回反复，其最终的平均电流为0，那为什么还能传输能量呢？有兴趣的同学可以再回顾：《电感特性原理》章节中关于坡印亭矢量的解释。

2，全桥拓扑原理

半桥拓扑最大输出功率由最大初级电流峰值和开关管承受最大关断电压决定，虽然半桥拓扑最大输出功率可以支持到1KW以上，但是当电源输出功率大于500W时，考虑大电流导致的开关管压降（损耗）以及器件成本，就需要考虑使用功率加倍的半桥改进拓扑——全桥拓扑。

2.1全桥拓扑结构和特点

全桥拓扑结构如下左图所示，有如下特点：

1. 变压器原边绕组施加的电压幅值是±Vdc而非半桥±Vdc/2，但开关管承受的关断电压与半桥拓扑相同（Vdc），所以在开关管承受相同峰值电流和电压条件下，全桥拓扑是半桥拓扑输出功率的2倍；

——如之前分析，由伏秒积公式可得，施加在线圈上的电压加倍，那么在相同时间下的伏秒积加倍（ΔV*Δt= L*ΔI），那么相同电感量的线圈存储/转换的磁场能量也加倍。

2. 全桥拓扑变压器原边所承受电压是半桥的2倍，所以其原边绕组数量是半桥拓扑的2倍，当输出功率和输入直流电压相同时全桥拓扑初级电流峰值和有效值是半桥拓扑的一半；

3. 相同输出功率下全桥和半桥拓扑变压器的大小是一样的，若使用较大体积变压器，全桥拓扑可在相同开关管电流和额定电压下得到2倍于半桥拓扑的输出功率。

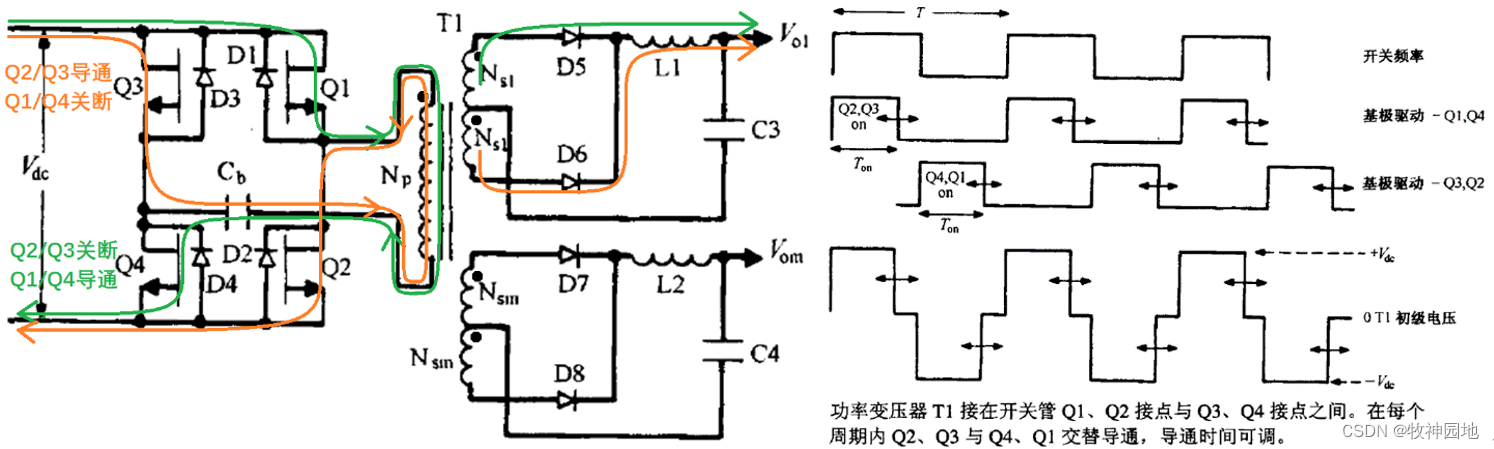
全桥拓扑电源的Q1/Q3和Q2/Q4分别串接于变压器原边的顶端和底端，结构分析如下：

1. 忽略Cb，在Q1/Q3和Q2/Q4分别导通时，原边绕组异名端分别接至GND和Vdc，而原边绕组的同名端分别接至Vdc和GND，所以全桥拓扑变压器原边绕组电压变化范围是±Vdc，是半桥拓扑的一半；

2. 同半桥拓扑一样， Q1/Q4和Q2/Q3不能同时导通，开关管Q1/Q4和Q2/Q3轮流导通半个周期，需要增加Q1/Q4和Q2/Q3的死区时间，设置导通时间Ton为80%的半周期；

3. Q1/Q4导通时， Q3的关断电压是Vdc（Vdc-(Vds-0) =Vdc-Vds ≈ Vdc），同理Q2的关断电压也是Vdc（(Vdc-Vds)-0= Vdc-Vds ≈ Vdc）；同理Q2/Q3导通时： Q1和Q4承受的最大电压也为Vdc。

在开关管导通和关断时不同节点电压/电流如上右图所示，全桥拓扑工作过程如下：

1. Q1/Q4导通而Q2/Q3关断时：

1, Np同名端电压为Vdc，异名端电压为GND，所以变压器原边绕组Np两端电压为：Vdc，电流通过Q1，T1，Cb和Q4流到GND；

2, 变压器原边Np以及幅边Ns1和Ns2的同名端相对于异名端为正，整流二极管D5正向偏置，电流从Ns1同名端通过D5和L1输入C3滤波电容器和负载。

2. Q1/Q4关断而Q2/Q3导通时：

1, Np同名端电压为0V，异名端电压为Vdc，变压器原边绕组Np两端电压为：-Vdc，C1与Cb串联接至Vdc，电流通过Q3，Cb， T1和Q2流到GND；；

2, 由于变压器T1原边绕组Np被施加了反向电压（-Vdc），此时所有绕组原/副边的同名端相对异名端为负，整流二极管D6正向偏置，电流从同名端通过D6和L1输入C3滤波电容器和负载。

3. 输入电压或负载电流变化时，反馈环检测Vom的变化，并调制脉宽Ton，以维持Vom不变；假设开关管导通电压为Vds，输出肖特基二极管压降为Vd，那么输出电压：Vom=[(Vdc-2*Vds)*Nsm/Np - Vd]*(2*Ton)/T，可得Vom ≈ Vdc*(Nsm/Np)*(2*Ton/T)。