2023年的深度学习入门指南(9) - SIMD和通用GPU编程
深度学习从一开始就跟GPU有不解之缘,因为算力是深度学习不可或缺的一部分。
时至今日,虽然多任务编程早已经深入人心,但是很多同学还没有接触过CPU上的SIMD指令,更不用说GPGPU的编程。这一篇我们先给SIMD和GPU编程扫个盲,让大家以后用到的时候有个感性认识。
CPU世界

从多线程说起
曾经的编程语言是不支持多线程的,需要操作系统和库来提供多线程能力,比如pthread库。时至今日,默认不支持多线程的平台还是有的,比如wasm。
1995年问世的Java语言从1.0开始就支持多线程,虽然一直到5.0版本才对多线程有重大改进。C++语言从C++11开始语言支持多线程了。
我们来看一个用C++多线程来实现矩阵乘法的例子:
#include <mutex>
#include <thread>
// 矩阵维度
const int width = 4;
// 矩阵
int A[width][width] = {
{1, 2, 3, 4},
{5, 6, 7, 8},
{9, 10, 11, 12},
{13, 14, 15, 16}
};
int B[width][width] = {
{1, 0, 0, 0},
{0, 1, 0, 0},
{0, 0, 1, 0},
{0, 0, 0, 1}
};
int C[width][width] = {0};
// 互斥锁
std::mutex mtx;
// 计算线程
void calculate(int row) {
for (int col = 0; col < width; col++) {
if (row < width && col < width) {
mtx.lock();
C[row][col] = A[row][col] + B[row][col];
mtx.unlock();
}
}
}
int main() {
// 创建线程
std::thread t1(calculate, 0);
std::thread t2(calculate, 1);
std::thread t3(calculate, 2);
std::thread t4(calculate, 3);
// 等待线程结束
t1.join();
t2.join();
t3.join();
t4.join();
// 打印结果
for (int i = 0; i < width; i++) {
for (int j = 0; j < width; j++) {
printf("%d ", C[i][j]);
}
printf("\n");
}
}
我们给它配上一个CMakeLists.txt:
cmake_minimum_required(VERSION 3.10)
# Set the project name
project(MatrixAddO)
# Set the C++ standard
set(CMAKE_CXX_STANDARD 11)
set(CMAKE_CXX_STANDARD_REQUIRED True)
# Add the executable
add_executable(matrix_add matadd.cpp)
这个代码大家应该都比较熟悉,就不多解释了。现在支持C++11以上已经是标配了。
OpenMP
早在线程写进C++11标准之前,就有很多并发编程的框架了,比如MPI和OpenMP.
OpenMP是一套支持跨平台共享内存方式的多线程并发的编程API,使用C, C++和Fortran语言,可以在多种处理器体系和操作系统中运行。它由OpenMP Architecture Review Board (ARB)牵头提出,并由多家计算机硬件和软件厂商共同定义和管理。
OpenMP最早是1997年发布的,当时只支持Fortran语言。1998年开始支持C/C++.
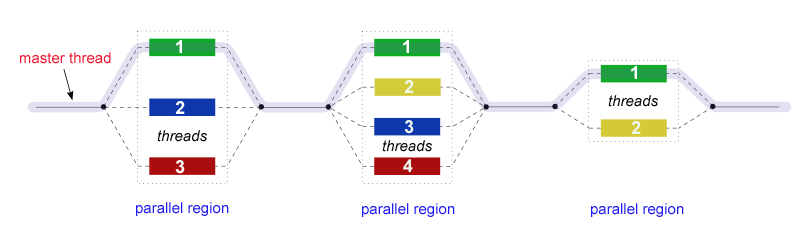
我们来看看用OpenMP如何实现矩阵的并发计算:
#include <iostream>
#include <omp.h>
#include <vector>
std::vector<std::vector<int>>
matrixAdd(const std::vector<std::vector<int>> &A,
const std::vector<std::vector<int>> &B) {
int rows = A.size();
int cols = A[0].size();
std::vector<std::vector<int>> C(rows, std::vector<int>(cols));
#pragma omp parallel for collapse(2)
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
C[i][j] = A[i][j] + B[i][j];
}
}
return C;
}
int main() {
std::vector<std::vector<int>> A = {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}};
std::vector<std::vector<int>> B = {{9, 8, 7}, {6, 5, 4}, {3, 2, 1}};
std::vector<std::vector<int>> C = matrixAdd(A, B);
for (const auto &row : C) {
for (int val : row) {
std::cout << val << " ";
}
std::cout << std::endl;
}
return 0;
}
#pragma omp parallel for collapse(2) 是一个 OpenMP 编译指令,用于表示一个并行区域,其中嵌套的循环将并行执行。让我们详细解释这个指令的各个部分:
#pragma omp:这是一个编译指令,表示接下来的代码将使用 OpenMP 进行并行化。
parallel for:这是一个组合指令,表示接下来的 for 循环将在多个线程上并行执行。每个线程将处理循环的一部分,从而加速整个循环的执行。
collapse(2):这是一个可选子句,用于指示嵌套循环的并行化。在这个例子中,collapse(2) 表示将两层嵌套的循环(即外层和内层循环)合并为一个并行循环。这样可以更好地利用多核处理器的性能,因为并行度增加了。
在我们的矩阵加法示例中,#pragma omp parallel for collapse(2) 指令应用于两个嵌套的 for 循环,它们分别遍历矩阵的行和列。使用此指令,这两个循环将合并为一个并行循环,从而在多核处理器上实现更高的性能。
需要注意的是,为了在程序中使用 OpenMP,你需要使用支持 OpenMP 的编译器(如 GCC 或 Clang),并在编译时启用 OpenMP 支持(如在 GCC 中使用 -fopenmp 标志)。
我们来写个支持OpenMP的CMakeLists.txt:
cmake_minimum_required(VERSION 3.10)
# Set the project name
project(MatrixAddOpenMP)
# Set the C++ standard
set(CMAKE_CXX_STANDARD 11)
set(CMAKE_CXX_STANDARD_REQUIRED True)
# Find OpenMP
find_package(OpenMP REQUIRED)
# Add the executable
add_executable(matrix_add main.cpp)
# Link OpenMP to the executable
if(OpenMP_CXX_FOUND)
target_link_libraries(matrix_add PUBLIC OpenMP::OpenMP_CXX)
endif()
可见,用了OpenMP的for循环,就可以变串行为并行。从而大大简化并行编程的难度。
SIMD
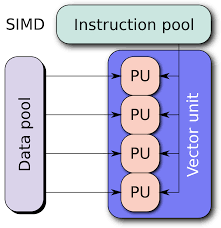
虽然多线程和OpenMP看起来都不错,都容易编程,但是,我们的优化并不是以简化编程为目的的。
虽然我们抱怨Intel是牙膏厂,每年的进步越来越有限。不过,还总是有新的指令增加到新的架构中来。这其中就有越来越强大的SIMD指令。
SIMD就是一条机器指令可以实现多条数据的操作。在Intel平台上,早在1997年就推出了64位的MMX指令集。1999年又有了128位的SSE指令集。2011年,又推出了256位的AVX(Advanced Vector Extensions)指令,我们来个例子看看:
#include <iostream>
#include <immintrin.h> // 包含 AVX 指令集头文件
void matrix_addition_avx(float* A, float* B, float* C, int size) {
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j += 8) { // 每次处理 8 个元素(AVX 可以处理 256 位,即 8 个单精度浮点数)
__m256 vecA = _mm256_loadu_ps(&A[i * size + j]);
__m256 vecB = _mm256_loadu_ps(&B[i * size + j]);
__m256 vecC = _mm256_add_ps(vecA, vecB);
_mm256_storeu_ps(&C[i * size + j], vecC);
}
}
}
int main() {
int size = 8; // 假设矩阵大小为 8x8
float A[64] = { /* ... */ }; // 初始化矩阵 A
float B[64] = { /* ... */ }; // 初始化矩阵 B
float C[64] = { 0 }; // 结果矩阵 C
matrix_addition_avx(A, B, C, size);
// 输出结果
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
std::cout << C[i * size + j] << " ";
}
std::cout << std::endl;
}
return 0;
}
我们来解释一下使用SIMD的几条语句:
__m256 vecA = _mm256_loadu_ps(&A[i * size + j]):从矩阵 A 中加载 8 个浮点数(一次性处理 256 位数据),存储在一个名为 vecA 的 __m256 类型变量中。
__m256 vecB = _mm256_loadu_ps(&B[i * size + j]):同样地,从矩阵 B 中加载 8 个浮点数,存储在一个名为 vecB 的 __m256 类型变量中。
__m256 vecC = _mm256_add_ps(vecA, vecB):使用 AVX 指令 _mm256_add_ps 对 vecA 和 vecB 中的浮点数分别进行逐元素加法,并将结果存储在名为 vecC 的 __m256 类型变量中。
_mm256_storeu_ps(&C[i * size + j], vecC):将 vecC 中的 8 个加法结果存储回矩阵 C 的相应位置。
这段代码使用了 AVX 指令集,实现了对浮点矩阵的加法运算。请注意,为了充分利用 AVX 的并行处理能力,矩阵尺寸应该是 8 的倍数。如果矩阵尺寸不是 8 的倍数,需要添加额外的逻辑来处理剩余的元素。
后来,Intel又推出了AVX2指令集,不过对于我们上边的代码并没有太多优化,而主要优化是在整数方面。
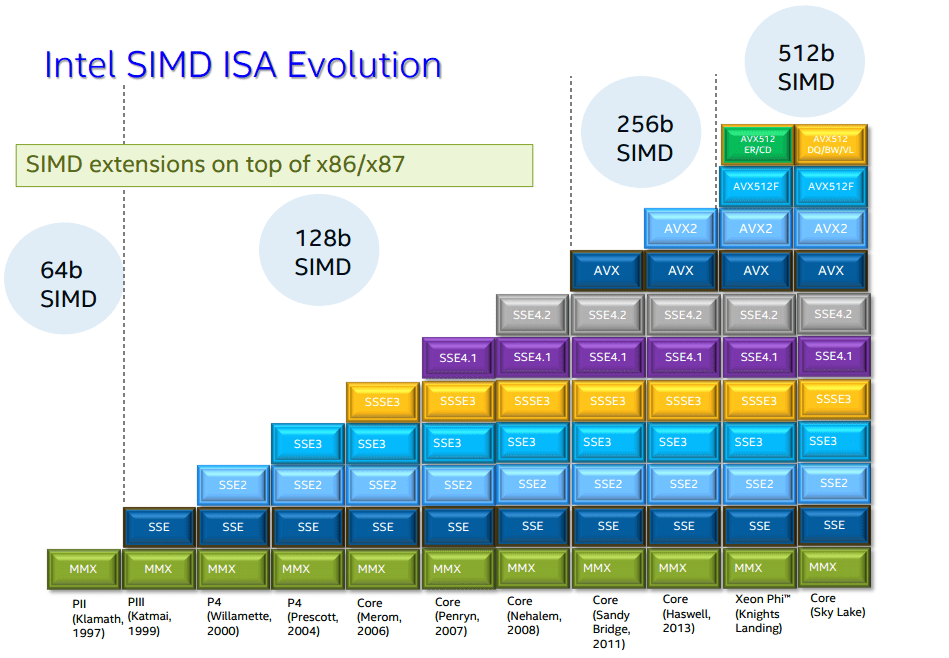
上节我们学习的量化和解量化就用上了,我们这次使用AVX2提供的整数计算的加速来实现:
#include <iostream>
#include <immintrin.h> // 包含 AVX2 指令集头文件
void matrix_addition_avx2_int(int *A, int *B, int *C, int size) {
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j += 8) { // 每次处理 8 个元素(AVX2 可以处理 256 位,即 8 个 int32 整数)
__m256i vecA = _mm256_loadu_si256((__m256i *)&A[i * size + j]);
__m256i vecB = _mm256_loadu_si256((__m256i *)&B[i * size + j]);
__m256i vecC = _mm256_add_epi32(vecA, vecB);
_mm256_storeu_si256((__m256i *)&C[i * size + j], vecC);
}
}
}
int main() {
int size = 8; // 假设矩阵大小为 8x8
int A[64] = { /* ... */ }; // 初始化矩阵 A
int B[64] = { /* ... */ }; // 初始化矩阵 B
int C[64] = {0}; // 结果矩阵 C
matrix_addition_avx2_int(A, B, C, size);
// 输出结果
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
std::cout << C[i * size + j] << " ";
}
std::cout << std::endl;
}
return 0;
}
我们不惜折腾量化一把转换成整数的原因是,AVX中只有_mm_add_epi32指令,只能对两个128位整数向量的逐元素相加,而_mm256_add_epi32是256位,数据量加倍了。
不只是加法,AVX2 提供了一系列针对整数操作的新指令,例如乘法、位操作和打包/解包操作等。
AVX2指令的执行吞吐量(throughput)一般为1指令/周期,而AVX1为2指令/周期。所以在同频率下,AVX2的整数加法指令性能理论上可以提高一倍。
同时, 与其他AVX2指令结合使用,如_mm256_load_si256或_mm256_store_si256等,来从内存中加载或存储向量,这样可以提高内存访问的性能和带宽。
后来,Intel还推出了AVX512指令,基本上就把AVX1中的256换成512就可以了:
#include <iostream>
#include <immintrin.h> // 包含 AVX-512 指令集头文件
void matrix_addition_avx512(float *A, float *B, float *C, int size) {
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j += 16) { // 每次处理 16 个元素(AVX-512 可以处理 512 位,即 16 个单精度浮点数)
__m512 vecA = _mm512_loadu_ps(&A[i * size + j]);
__m512 vecB = _mm512_loadu_ps(&B[i * size + j]);
__m512 vecC = _mm512_add_ps(vecA, vecB);
_mm512_storeu_ps(&C[i * size + j], vecC);
}
}
}
int main() {
int size = 16; // 假设矩阵大小为 16x16
float A[256] = { /* ... */ }; // 初始化矩阵 A
float B[256] = { /* ... */ }; // 初始化矩阵 B
float C[256] = {0}; // 结果矩阵 C
matrix_addition_avx512(A, B, C, size);
// 输出结果
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
std::cout << C[i * size + j] << " ";
}
std::cout << std::endl;
}
return 0;
}
但是,优化并不总是一根筋地往上堆指令就可以的,AVX512是一种非常耗电的指令集,此时我们需要实测权衡一下。
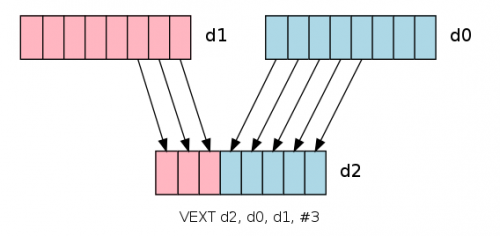
针对手机上用的ARM CPU,可以使用NEON指令来实现SIMD功能:
#include <stdio.h>
#include <arm_neon.h>
void matrix_addition_neon(float *A, float *B, float *C, int size) {
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j += 4) { // 每次处理 4 个元素(NEON 可以处理 128 位,即 4 个单精度浮点数)
float32x4_t vecA = vld1q_f32(&A[i * size + j]);
float32x4_t vecB = vld1q_f32(&B[i * size + j]);
float32x4_t vecC = vaddq_f32(vecA, vecB);
vst1q_f32(&C[i * size + j], vecC);
}
}
}
int main() {
int size = 4; // 假设矩阵大小为 4x4
float A[16] = { /* ... */ }; // 初始化矩阵 A
float B[16] = { /* ... */ }; // 初始化矩阵 B
float C[16] = {0}; // 结果矩阵 C
matrix_addition_neon(A, B, C, size);
// 输出结果
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
printf("%f ", C[i * size + j]);
}
printf("\n");
}
return 0;
}
对于初接触汇编级优化的同学,可能感觉很新鲜。不过,挑战更大的在后面,我们要进入GPU的世界了。
GPU世界
欢迎来到异构计算的世界。之前我们的代码不管怎么写,都是在CPU上运行的。
从这一时刻开始,不管什么技术,我们都是由CPU和GPU两部分代码共同组合的了。
我们先从目前看仍然是主力的CUDA开始。

CUDA
CUDA 1.0于2007年发布。目前CUDA版本为12.1。
目前广泛适配的是CUDA 11.x,现在较新的版本为CUDA 11.8。因为CUDA 11.x才支持A100为代表的安培架构的GPU。3060,3070,3080,3090也是安培架构的GPU。
2080, 2060, 1660这一系列的是图灵架构,对应的是CUDA 10.x版本。
1060,1080这一系列对应的是帕斯卡架我,对应的是CUDA 8.0版本。
在CUDA中,运行在GPU上的代码我们叫做核函数。
我们先完整地看下这个代码,然后再解释。
#include "cuda_runtime.h"
#include "device_launch_parameters.h"
#include <iostream>
// 矩阵加法的CUDA核函数
__global__ void matrixAdd10(int* A, int* B, int* C, int width) {
int row = blockIdx.y * blockDim.y + threadIdx.y;
int col = blockIdx.x * blockDim.x + threadIdx.x;
if (row < width && col < width) {
C[row * width + col] = A[row * width + col] + B[row * width + col];
}
}
int main() {
// 矩阵维度
int width = 4;
// 分配CPU内存
int* A, * B, * C;
A = (int*)malloc(width * width * sizeof(int));
B = (int*)malloc(width * width * sizeof(int));
C = (int*)malloc(width * width * sizeof(int));
// 初始化A和B矩阵
for (int i = 0; i < width; i++) {
for (int j = 0; j < width; j++) {
A[i * width + j] = i;
B[i * width + j] = j;
}
}
// 为GPU矩阵分配内存
int* d_A, * d_B, * d_C;
cudaMalloc((void**)&d_A, width * width * sizeof(int));
cudaMalloc((void**)&d_B, width * width * sizeof(int));
cudaMalloc((void**)&d_C, width * width * sizeof(int));
// 将矩阵从CPU内存复制到GPU内存
cudaMemcpy(d_A, A, width * width * sizeof(int), cudaMemcpyHostToDevice);
cudaMemcpy(d_B, B, width * width * sizeof(int), cudaMemcpyHostToDevice);
// 配置CUDA核函数参数
dim3 threads(width, width);
dim3 grid(1, 1);
matrixAdd10 <<<grid, threads >>> (d_A, d_B, d_C, width);
// 等待CUDA核函数执行完毕
cudaDeviceSynchronize();
// 将结果从GPU内存复制到CPU内存
cudaMemcpy(C, d_C, width * width * sizeof(int), cudaMemcpyDeviceToHost);
// 验证结果
for (int i = 0; i < width; i++) {
for (int j = 0; j < width; j++) {
if (C[i * width + j] != i + j) {
printf("错误!");
return 0;
}
}
}
printf("矩阵加法成功!");
// 释放CPU和GPU内存
free(A); free(B); free(C);
cudaFree(d_A); cudaFree(d_B); cudaFree(d_C);
}
其实,CPU部分的main函数还是比较好懂的。核函数这边就有点不知所措了,比如下面这两行:
int row = blockIdx.y * blockDim.y + threadIdx.y;
int col = blockIdx.x * blockDim.x + threadIdx.x;
这两行代码用于计算当前 CUDA 线程在二维矩阵中的位置。在 CUDA 编程模型中,我们通常将问题划分为多个线程块 (block),每个线程块包含多个线程。线程块和线程可以是一维、二维或三维的。在这个矩阵加法的例子中,我们使用二维线程块和二维线程。
blockIdx 和 blockDim 分别表示线程块索引和线程块的尺寸,它们都是 dim3 类型的变量。threadIdx 表示线程的索引,也是一个 dim3 类型的变量。x 和 y 分别表示这些变量的横向和纵向分量。
int row = blockIdx.y * blockDim.y + threadIdx.y;
这行代码计算当前线程在二维矩阵中的行号。blockIdx.y 表示当前线程所在的线程块在纵向(行方向)上的索引,blockDim.y 表示每个线程块在纵向上包含的线程数,threadIdx.y 表示当前线程在所在线程块中纵向的索引。将这些值组合在一起,可以计算出当前线程在整个矩阵中的行号。
int col = blockIdx.x * blockDim.x + threadIdx.x;
这行代码计算当前线程在二维矩阵中的列号。blockIdx.x 表示当前线程所在的线程块在横向(列方向)上的索引,blockDim.x 表示每个线程块在横向上包含的线程数,threadIdx.x 表示当前线程在所在线程块中横向的索引。将这些值组合在一起,可以计算出当前线程在整个矩阵中的列号。
通过这两行代码,我们可以为每个线程分配一个特定的矩阵元素,让它执行相应的加法操作。这种并行计算方式可以显著提高矩阵加法的计算速度。
这段代码需要使用NVidia CUDA工具包中的nvcc来编译了,我们将其存为matrix_add.cu:
nvcc -o matrix_add matrix_add.cu
./matrix_add
OpenCL
CUDA是一门NVidia专有的技术,在其它GPU上用不了。所以其它厂商一直在想办法提供类似的技术。这其中,曾经最被看好的就是OpenCL。OpenCL由Apple最初提出并由Khronos Group牵头制定和管理标准。
OpenCL是一种用于编写跨平台的异构计算程序的框架,支持使用C99, C++14和C++17语言编写代码,可以在多种处理器和操作系统上运行,如CPU, GPU, DSP, FPGA等。
OpenCL的第一个版本于2008年发布。
我们来看下用OpenCL写的计算矩阵加法的节选。
首先也是运行在GPU上的核函数,然后通过enqueueNDRangeKernel将其放入执行队列中。
#include <iostream>
#include <vector>
#include <CL/cl.hpp>
const char* kernelSource = R"CLC(
__kernel void matrix_add(__global const int* A, __global const int* B, __global int* C, int rows, int cols) {
int i = get_global_id(0);
int j = get_global_id(1);
int index = i * cols + j;
if (i < rows && j < cols) {
C[index] = A[index] + B[index];
}
}
)CLC";
int main() {
std::vector<std::vector<int>> A = {
{1, 2, 3},
{4, 5, 6},
{7, 8, 9}
};
std::vector<std::vector<int>> B = {
{9, 8, 7},
{6, 5, 4},
{3, 2, 1}
};
int rows = A.size();
int cols = A[0].size();
std::vector<int> A_flat(rows * cols), B_flat(rows * cols), C_flat(rows * cols);
for (int i = 0; i < rows; ++i) {
for (int j = 0; j < cols; ++j) {
A_flat[i * cols + j] = A[i][j];
B_flat[i * cols + j] = B[i][j];
}
}
std::vector<cl::Platform> platforms;
cl::Platform::get(&platforms);
cl_context_properties properties[] = {
CL_CONTEXT_PLATFORM, (cl_context_properties)(platforms[0])(), 0
};
cl::Context context(CL_DEVICE_TYPE_GPU, properties);
cl::Program program(context, kernelSource, true);
cl::CommandQueue queue(context);
cl::Buffer buffer_A(context, CL_MEM_READ_ONLY, sizeof(int) * rows * cols);
cl::Buffer buffer_B(context, CL_MEM_READ_ONLY, sizeof(int) * rows * cols);
cl::Buffer buffer_C(context, CL_MEM_WRITE_ONLY, sizeof(int) * rows * cols);
queue.enqueueWriteBuffer(buffer_A, CL_TRUE, 0, sizeof(int) * rows * cols, A_flat.data());
queue.enqueueWriteBuffer(buffer_B, CL_TRUE, 0, sizeof(int) * rows * cols, B_flat.data());
cl::Kernel kernel(program, "matrix_add");
kernel.setArg(0, buffer_A);
kernel.setArg(1, buffer_B);
kernel.setArg(2, buffer_C);
kernel.setArg(3, rows);
kernel.setArg(4, cols);
cl::NDRange global_size(rows, cols);
queue.enqueueNDRangeKernel(kernel, cl::NullRange, global_size);
queue.enqueueReadBuffer(buffer_C, CL_TRUE, 0, sizeof(int) * rows * cols, C_flat.data());
std::vector<std::vector<int>> C(rows, std::vector<int>(cols));
for (int i = 0; i < rows; ++i) {
for (int j = 0; j < cols; ++j) {
C[i][j] = C_flat[i * cols + j];
}
}
...
Direct3D
在Windows上,我们都知道微软的主要用于游戏开发的DirectX。
Direct X作为Windows直接访问硬件的游戏加速接口,早在1995年就推出了。不过Direct X 1.0的时候还不支持3D,只支持2D。因为第一个广泛使用的3D加速卡3dfx Voodoo卡1996年才推出。
Direct3D 1.0于1996年问世。不过这时候只是对标OpenGL的框架,跟GPGPU关系还远着呢。
一直要到2009年,Windows 7时代的Direct3D 11.0,才正式可以支持计算着色器。Direct 3D 12.0于2015年和Windows 10同时代推出。

在Direct3D 12中,GPU指令是通过HLSL语言来写的:
// MatrixAddition.hlsl
[numthreads(16, 16, 1)]
void main(uint3 dt : SV_DispatchThreadID, uint3 gt : SV_GroupThreadID, uint3 gi : SV_GroupID) {
// 确保我们在矩阵范围内
if (dt.x >= 3 || dt.y >= 3) {
return;
}
// 矩阵 A 和 B 的值
float A[3][3] = {
{1, 2, 3},
{4, 5, 6},
{7, 8, 9}
};
float B[3][3] = {
{9, 8, 7},
{6, 5, 4},
{3, 2, 1}
};
// 计算矩阵加法
float result = A[dt.y][dt.x] + B[dt.y][dt.x];
// 将结果写入输出缓冲区
RWStructuredBuffer<float> output;
output[dt.y * 3 + dt.x] = result;
}
然后是CPU上的操作,要建立一个计算着色器,因为细节比较多,我就略去了,只写主干:
#include <d3d12.h>
#include <d3dcompiler.h>
#include <iostream>
// 创建一个简单的计算着色器的 PSO
ID3D12PipelineState* CreateMatrixAdditionPSO(ID3D12Device* device) {
ID3DBlob* csBlob = nullptr;
D3DCompileFromFile(L"MatrixAddition.hlsl", nullptr, nullptr, "main", "cs_5_0", 0, 0, &csBlob, nullptr);
D3D12_COMPUTE_PIPELINE_STATE_DESC psoDesc = {};
psoDesc.pRootSignature = rootSignature; // 假设已创建好根签名
psoDesc.CS = CD3DX12_SHADER_BYTECODE(csBlob);
ID3D12PipelineState* pso = nullptr;
device->CreateComputePipelineState(&psoDesc, IID_PPV_ARGS(&pso));
csBlob->Release();
return pso;
}
// 执行矩阵加法计算
void RunMatrixAddition(ID3D12GraphicsCommandList* commandList, ID3D12Resource* outputBuffer) {
commandList->SetPipelineState(matrixAdditionPSO);
commandList->SetComputeRootSignature(rootSignature);
commandList->SetComputeRootUnorderedAccessView(0, outputBuffer->GetGPUVirtualAddress());
// 分发计算着色器,设置线程组的数量
commandList->Dispatch(1, 1, 1);
// 确保在继续之前完成计算操作
commandList->ResourceBarrier(1, &CD3DX12_RESOURCE_BARRIER::UAV(outputBuffer));
}
int main() {
// 初始化 DirectX 12 设备、命令队列、命令分配器等...
// ...
// 创建根签名、PSO 和计算着色器相关资源
// ...
// 创建输出缓冲区
ID3D12Resource* outputBuffer = nullptr;
device->CreateCommittedResource(
&CD3DX12_HEAP_PROPERTIES(D3D12_HEAP_TYPE_DEFAULT),
D3D12_HEAP_FLAG_NONE,
&CD3DX12_RESOURCE_DESC::Buffer(3 * 3 * sizeof(float)),
D3D12_RESOURCE_STATE_UNORDERED_ACCESS,
nullptr,
IID_PPV_ARGS(&outputBuffer)
);
// 创建并执行命令列表
ID3D12GraphicsCommandList* commandList = nullptr;
device->CreateCommandList(0, D3D12_COMMAND_LIST_TYPE_DIRECT, commandAllocator, nullptr, IID_PPV_ARGS(&commandList));
RunMatrixAddition(commandList, outputBuffer);
// 关闭命令列表并执行
commandList->Close();
ID3D12CommandList* commandLists[] = {commandList};
commandQueue->ExecuteCommandLists(_countof(commandLists), commandLists);
// 同步 GPU 和 CPU
// ...
// 从输出缓冲区中读取结果
float result[3][3] = {};
void* mappedData = nullptr;
outputBuffer->Map(0, nullptr, &mappedData);
memcpy(result, mappedData, sizeof(result));
outputBuffer->Unmap(0, nullptr);
// 输出结果
for (int i = 0; i < 3; ++i) {
for (int j = 0; j < 3; ++j) {
std::cout << result[i][j] << " ";
}
std::cout << std::endl;
}
// 清理资源
// ...
}
Vulkan

Vulkan由Khronos Group牵头制定和管理标准,是OpenGL的继任者。它最早的技术来自于AMD。
Vulkan是一种用于编写跨平台的图形和计算程序的框架,支持使用C和C++语言编写代码,可以在多种处理器和操作系统上运行,如CPU, GPU, DSP, FPGA等。
Vulkan的1.0版本于2016年发布。
默认情况下,Vulkan使用带计算管线的glsl:
#version 450
#extension GL_ARB_separate_shader_objects : enable
layout (local_size_x = 16, local_size_y = 16, local_size_z = 1) in;
layout (binding = 0) readonly buffer InputA {
float dataA[];
};
layout (binding = 1) readonly buffer InputB {
float dataB[];
};
layout (binding = 2) writeonly buffer Output {
float dataC[];
};
void main() {
uint index = gl_GlobalInvocationID.x + gl_GlobalInvocationID.y * gl_NumWorkGroups.x * gl_WorkGroupSize.x;
dataC[index] = dataA[index] + dataB[index];
}
然后,在主机程序中,完成以下步骤:
- 初始化Vulkan实例和物理/逻辑设备。
- 创建一个Vulkan计算管道,加载和编译计算着色器。
- 为输入矩阵A和B以及输出矩阵C创建Vulkan缓冲区。
- 将输入矩阵数据复制到输入缓冲区。
- 创建描述符集布局和描述符池,以描述着色器中的资源绑定。
- 创建描述符集,并将输入/输出缓冲区绑定到描述符集中。
- 创建一个Vulkan命令缓冲区,以记录计算着色器调度的命令。
- 开始记录命令缓冲区,并调用vkCmdBindPipeline和vkCmdBindDescriptorSets将计算管道和描- 述符集绑定到命令缓冲区。
- 使用vkCmdDispatch调度计算着色器执行矩阵加法。
- 结束命令缓冲区记录,将命令缓冲区提交到Vulkan队列。
- 等待队列执行完成,并将输出缓冲区的数据复制回主机内存。
- 清理Vulkan资源。
具体代码就不详细列出了。
大致的代码结构为:
// Vulkan实例、设备、命令池、队列
VkInstance instance;
VkDevice device;
VkCommandPool commandPool;
VkQueue queue;
// 矩阵维度
const int width = 4;
// 顶点缓冲区对象
VkBuffer vertexBuffer;
VkDeviceMemory vertexBufferMemory;
// 结果缓冲区对象
VkBuffer resultBuffer;
VkDeviceMemory resultBufferMemory;
// 着色器模块和管线
VkShaderModule shaderModule;
VkPipeline pipeline;
// 创建顶点缓冲区
// 向缓冲区填充矩阵A和B
// ...
// 创建结果缓冲区
// 向缓冲区映射内存
void* resultData;
vkMapMemory(device, resultBufferMemory, 0, sizeof(int) * 4 * 4, 0, &resultData);
// 创建着色器模块(矩阵加法着色器)
const char* shaderCode = "上面的glsl";
shaderModule = createShaderModule(shaderCode);
// 创建图形管线
// ...
// 记录命令
VkCommandBuffer commandBuffer;
VkCommandBufferAllocateInfo commandBufferAllocateInfo = ...;
vkAllocateCommandBuffers(commandPool, &commandBufferAllocateInfo, &commandBuffer);
// 开始记录命令
vkBeginCommandBuffer(commandBuffer, &beginInfo);
// 绑定顶点缓冲区和结果缓冲区
vkCmdBindVertexBuffers(commandBuffer, 0, 1, &vertexBuffer, &offset);
vkCmdBindBuffer(commandBuffer, 1, 0, resultBuffer, &offset);
// 绘制
vkCmdDraw(commandBuffer, 4, 1, 0, 0);
// 结束记录命令
vkEndCommandBuffer(commandBuffer);
// 提交命令并执行
VkSubmitInfo submitInfo = ...;
vkQueueSubmit(queue, 1, &submitInfo, VK_NULL_HANDLE);
vkQueueWaitIdle(queue);
// 读取结果矩阵
for (int i = 0; i < width; i++) {
for (int j = 0; j < width; j++) {
int result = ((int*)resultData)[i * width + j];
printf("%d ", result);
}
printf("\n");
}
// 释放Vulkan资源
...
WebGPU
WebGPU是刚刚要被Chrome浏览器支持的用于前端的GPU技术。
WebGPU是一种用于编写跨平台的图形和计算程序的框架,支持使用JavaScript和WebAssembly语言编写代码,可以在多种浏览器和操作系统上运行,如Chrome, Firefox, Safari等。WebGPU是由W3C的GPU for the Web工作组制定和管理标准,是WebGL的继任者。
前面我们看到,源于NVidia技术的CUDA,源于Apple技术的OpenCL,源于微软技术的DirectX,还有源于AMD技术的Vulkan在桌面和服务端百花争艳。在移动端自然也是少不了龙争虎斗。
第一个提出WebGPU想法的是苹果,2016年2月,苹果公司提出了一个名为Web Metal的提案,旨在将Metal API的概念移植到Web平台上。
2017年2月,微软公司提出了一个名为Web D3D的提案,旨在将Direct3D 12 API的概念移植到Web平台上。
2017年8月,Mozilla公司提出了一个名为Obsidian的提案,旨在创建一个基于Vulkan API的抽象层。
几家争执不下,谷歌公司提出了一个名为NXT的提案,旨在创建一个基于Vulkan, Metal和Direct3D 12 API的抽象层。
2018年4月,W3C工作组决定将NXT作为规范草案的起点,并将其重命名为WebGPU。
既然是一个抽象层,着色器语言不管使用SPIR-V,Vulkan的GLSL,DirectX的HLSL或者苹果的Metal Shading Language就都不合适了。
于是2019年,WebGPU社区组提出了一个新的着色器语言的提案,名为WebGPU Shading Language (WGSL),旨在创建一个基于SPIR-V的文本格式,以提供一种安全、可移植、易于使用和易于实现的着色器语言。
下面的代码展示下流程,这个时刻还有浏览器正式支持。等子弹飞一会儿浏览器正式上线了之后,我们在后面会专门讲。
看下图:WebGPU的规范还没release呢。WGSL的规范也同样没有最后release。

js
// 获取WebGPU adapter和设备
const adapter = await navigator.gpu.requestAdapter();
const device = await adapter.requestDevice();
// 矩阵维度
const width = 4;
// 创建缓冲区 - 用作顶点缓冲区和结果缓冲区
const vertexBuffer = device.createBuffer({
size: width * width * 4 * Int32Array.BYTES_PER_ELEMENT,
usage: GPUBufferUsage.VERTEX | GPUBufferUsage.STORAGE
});
// 获得缓冲区映射 - 填充矩阵A和B
const vertexBufferMapping = await vertexBuffer.map();
new Int32Array(vertexBufferMapping).fill(/* A和B矩阵 */);
vertexBuffer.unmap();
// 着色器代码
const shaderCode = `
kernel void addMatrices(device int* a [[buffer(0)]],
device int* b [[buffer(1)]],
device int* c [[buffer(2)]]) {
const int width = 4;
int tid = threadIdx.x * 4 + threadIdx.y;
if (tid < width * width) {
c[tid] = a[tid] + b[tid];
}
}
`;
// 创建着色器模块
const shaderModule = device.createShaderModule({
code: shaderCode
});
// 运行着色器 - 执行矩阵加法
const pipeline = device.createComputePipeline({
compute: {
module: shaderModule,
entryPoint: "addMatrices"
}
});
const passEncoder = device.createCommandEncoder();
const computePass = passEncoder.beginComputePass();
computePass.setPipeline(pipeline);
computePass.setBuffer(0, vertexBuffer);
computePass.setBuffer(1, vertexBuffer);
computePass.setBuffer(2, vertexBuffer);
computePass.dispatch(1);
computePass.endPass();
device.queue.submit([passEncoder.finish()]);
// 读取结果
const result = new Int32Array(
await vertexBuffer.mapRead()
);
// 打印结果矩阵
...
// 释放资源
小结
虽然还没有讲细节,但是本篇为我们打开了SIMD和GPU编程的一扇门。





![[架构之路-190]-《软考-系统分析师》-4-据通信与计算机网络-5-图解CRC计算方法与步骤](https://img-blog.csdnimg.cn/6da120259ec7433581c7e7a634f21c8f.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBAcXFfNTI1MTQ3NTA=,size_20,color_FFFFFF,t_70,g_se,x_16#pic_center)