算法导论第三版，CH34笔记

NP完全性

Chapter Introduction

一般来说，我们认为可以在多项式时间内求解的问题是易处理的问题，在超多项式时间内解决的问题是不易处理的问题。

下面列出的几对问题，前者可以用多项式时间算法求解，后者是NP完全问题，他们很相近：

最短与最长简单路径

简单路径指的是没有重复顶点的路径
欧拉回路与汉密尔顿圈
- 欧拉回路：能够路过G中每一条边一次的圈。
- 汉密尔顿圈：包含图中每一个顶点的简单路径
2-CNF可满足性问题与3-CNF可满足性问题

CNF是合取范式的缩写（conjunction normal form），2CNF则是含有两个逻辑变量的合取范式。验证2-CNF是否是可满足式可在多项式时间内完成，但是验证3-CNF是否为可满足式无法在多项式时间内验证。

NP完全性与P类问题和NP类问题：

P类问题：能在多项式时间 $O(n^k)$ 内解决的问题，其中 $n$ 为问题的输入规模， $k$ 为某一常量。

NP类问题：能在多项式时间内被证明的问题。

“能被证明”即当我们已知一个问题解的证书（certificate），那么可以证明此问题在该输入规模下能在多项式时间内解决。

比如：汉密尔顿圈问题中，给定一个有向图 $G = (V, E)$ ，证书是一个含有 $∣ V ∣$ 个顶点的序列 $v_1,v_2,...,v_{|V|})$ ，我们可以轻易证明 $(v_i,v_{i+1})\in E,$ （其中 $i = 1, 2, 3, ..., ∣ V ∣ - 1$ ），即可以轻易判断该解是否有效。

**P问题与NP问题的关系：**所有的P问题都是NP问题。因为如果一个问题是P问题，那么不用任何证书，就能在多项式时间内求解，即有 $P\subseteq NP$ 。至于P问题是不是NP问题的真子集，在目前还是一个开放的问题。

NPC问题：如果一个NP问题A和其他任何NP问题一样“不易解决”，那么我们认为这一问题是NPC问题或者称之为NP完全问题。

关于P问题、NP问题、NPC问题的概念，将在后续小节中给出具体的定义。

要证明一个问题是NP完全问题，要依赖三个概念：

概念1：判定问题与最优化问题：很多有趣的问题是最优化问题（optimization problem），其中每个可行解都有一个关联的值。在最优化问题中就是要找出那个具有最优值的可行解。

最优解与最优解的值

NP完全性不适合直接应用于最优化问题，但适合应用于判定问题（decision problem），因为这种问题的答案是简单的“是”或“否”。

判定问题和最优化问题之间是存在联系的，可以利用这种联系将一个给定的最优化问题转换为一个判定问题。【给优化的值强加一个界】

比如在最短路径问题中，我们会判断 $u$ 和 $v$ 之间是否存在一条至多包含 $k$ 条边的路径

概念2：规约

规约算法是这样的思想：

对于一个判定问题A，希望在多项式时间内求解这个问题。我们称某一个特定问题的输入为该问题的实例（instance）。设问题B是一个与A不同的判定问题，我们知道如何在多项式时间内求解它。最后假设有一个过程，他可以将任意一个A问题的实例 $\alpha$ 转换为问题B的具有以下特征的实例 $\beta$ ：

转换操作需要多项式时间
两个问题的解是相同的。即 $\alpha$ 的解是“是”，当且仅当 $\beta$ 的解是“是”。

我们将这样的过程称为多项式时间规约算法。它提供了一种在多项式时间内求解问题A的方法。
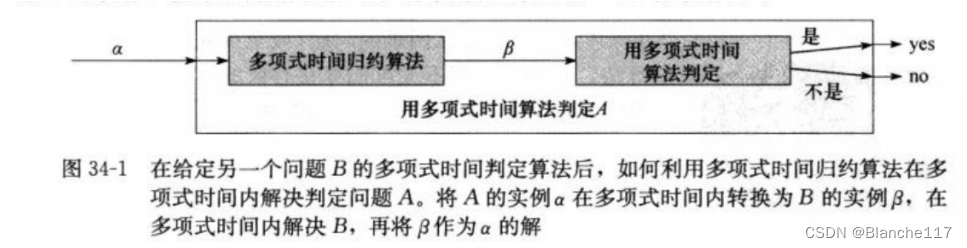
在这里插入图片描述

我们使用规约来证明一个问题求解的困难程度：假如一个已知的NPC问题A可在多项式时间内规约为一个未知的问题B，那么问题B的求解是不易于问题A的。这样就证明了求解问题B是困难的。

一、多项式时间与多项式时间的验证

多项式时间

我们认为多项式时间可解的问题是易处理的。

抽象问题

为理解多项式时间可解问题类（P问题），首先必须对所谓的“问题”这一概念进行形式化定义。

定义抽象问题Q为在问题实例集合I和问题解集合S上的一个二元关系。例如，在最短路径问题中，它的一个实例是是由一个图和两个顶点所组成的三元组。其解为图中的顶点序列，序列可能为空（两个顶点间可能不存在通路）。最短路径问题本身就是一个关系，它把图的每个实例和两个顶点与图中联系这两个顶点的最短路径联系在一起了，因为最短路径不一定是唯一的，所以一个给定的问题实例可能有多个解。

这里注意区别问题与问题实例的概念。

一个问题是NPC或者NP难的不意味他的所有实例都是NPC/NP难的。比如：

三色图问题是一个NPC问题，但是具体到某个实例：把图具体到树结构上，那么我们可以发现很容易就能找到该实例的解。
01整数规划问题是NPC问题，但是具体到某个实例：对于某些优化目标特殊的问题，它也可以很容易得到问题的解。

总结来说：一个问题是NP难的，意味着这个问题存在一些实例，这些实例是NP难的。而这个问题存在一些可以在多项式时间内求解的实例是完全可能的。

参考：complexity theory - Are all Integer Linear Programming problems NP-Hard? - Computer Science Stack Exchange ，很棒的回答

抽象问题的形式化定义比较笼统。NP完全理论集中在判定问题上，即解为“是”或者“否”的问题。可把抽象的判定问题看作从实例集合映射到解集{0,1}上的一个函数。

这种二元关系一定是函数，解不可能既是“是”又是“否”；但是上述抽象问题的形式定义解可能是多个的，因此只能说是二元关系，而不一定是函数

许多抽象问题不是判定问题，而是最优化问题。这些问题中，某些量必须被最大化或者最小化，而像上述introduction中最短路径的例子，将一个最优化问题转换一个判定问题并不困难，只需要给优化目标强加一个界即可转换成功。

编码

用计算机来求解一个抽象问题，必须用一种程序能够理解的方式来表示问题。抽象问题集合S的编码是从S到二进制串集合的映射e。

编码是一种表示抽象问题的映射

例如自然数 $N=\{0,1,2,3,4...\}$ 编码为串 $N=\{0,1,10,11,100...\}$ 。即使是一个复合对象，也可以把其组成部分的表示进行组合，从而把它编码为一个二进制串。多边形、图、函数、有序对等都能编码为二进制串。

或许可以类比一下结构体？

因此，求解一个抽象的判定问题，实际是把一个问题实例的编码作为输入。

背包问题似乎用动态规划法可以在多项式时间内得到问题的答案，但是这其实是把背包问题的输入看做一元的，而非二进制编码输入的。我们称这种算法为伪多项式时间算法。

具体问题：二进制串集合为实例集的问题。

这个定义很有趣，给人有种从计算机的角度定义的味道。我们把在问题实例集合I和问题解集合S上的一个二元关系称为抽象问题，把对应这个抽象问题的实例集编码为了二进制串，对人来说，看起来更抽象了，但实际上我们却称之为具体问题。很难不去认为这个定义是从计算机的角度出发的。

多项式时间可解的：如果当提供给算法的是长度为 $n = ∣ i ∣$ 的一个问题实例 $i$ 时，算法可以在 $O (T (n))$ 时间内产生问题的解，我们称该算法在 $O (T (n))$ 时间内解决了该问题。如果对于某个常数 $k$ ，存在一个能在 $O(n^k)$ 时间内求解出某具体问题的算法，就说该具体问题是多项式时间可解的。

结合上述说明，可以给出复杂类P的定义。

复杂类P：在多项式时间内可解的具体判定问题的集合。

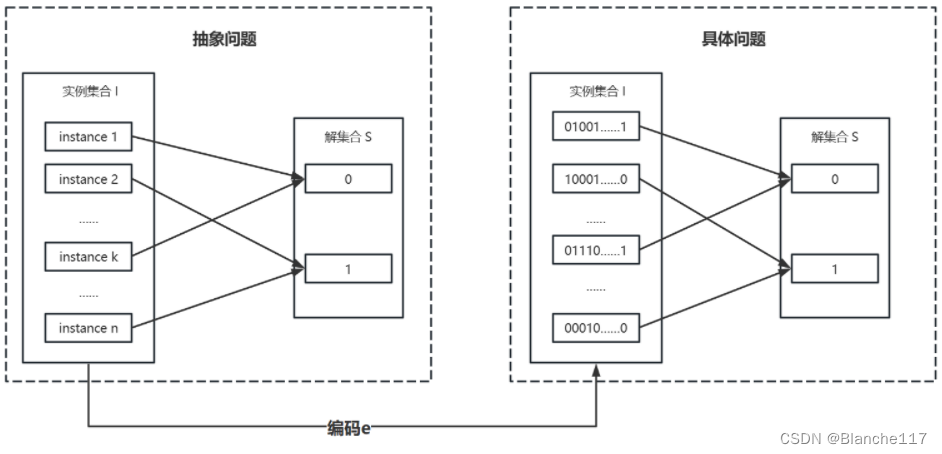
在这里插入图片描述

假定任何无意义的串都映射到0；再这样的前提下，具体问题与抽象问题同解。

我们希望求解一个问题的效率不应该依赖于问题的编码，这样多项式时间的可解性就从具体问题扩展到了抽象问题，但实际上这种依赖是非常严重的。

如：把一个整数 $k$ 作为算法的唯一输入，并假设算法的运行时间为 $\Theta(k)$ 。

如果提供的整数 $k$ 是一元的（即由 $k$ 个1组成的串），那么对长度为 $n$ 的输入，算法的运行时间为多项式时间 $O (n)$ 。
如果使用二进制来表示 $k$ ，则输入的长度为 $\lfloor \lg k\rfloor+1$ ，这种情况下，该算法的运行时间为 $\Theta(k)=\Theta(2^n)$ ，它与输入规模成指数关系。

因此，根据编码方式的不同，算法的运行时间是多项式时间或者超多项式时间。

一元编码(Unary coding)：对于整数2，表示为110,；整数3，表示为1110；即k个1后跟一个0的形式。

编码方式对问题求解的影响：对于一个抽象问题如何编码，对理解多项式时间是重要的。但实际上，如果不采用代价高昂的编码（如一元编码），那么问题的实际编码形式对问题是否能在多项式时间内求解是没有太大影响的。比如，对于用二进制和三进制编码的同一个抽象问题，二者可以很容易在多项式时间内互相转换，所以使用二进制还是三进制表示这个问题并不影响问题是否能在多项式时间内求解。

多项式时间可计算函数：对一个函数 $f:\{0,1\}^*\rightarrow \{0,1\}^*$ ，如果存在一个多项式时间的算法A，他对任何给定的输入 $x\in\{0,1\}^*$ ，都能产生输出 $f (x)$ ，则称该函数是一个多项式时间可计算函数。

编码的多项式相关：对某个问题的实例集I，如果存在两个多项式时间可计算函数 $f_{12}$ 和 $f_{21}$ 满足对任意的 $i\in I$ ，有 $f_{12}(e_1(i))=e_2(i)$ ，且 $f_{21}(e_2(i))=e_1(i)$ ，我们就说这两个编码是多项式相关的。也就是说，两个编码可由多项式时间相互转换。

反之：如果两个抽象问题的两种编码 $e_1$ 和 $e_2$ 是多项式相关的，如下面引理所述，该问题本身是否多项式时间可解与选用哪种编码无关。

**引理1：**设Q是定义在一个实例集I上的一个抽象判定问题， $e_1$ 与 $e_2$ 是I上多项式相关的编码，则 $e_1(Q)\in P$ 当且仅当 $e_2(Q)\in P$ 。

证明略。

本节的说明其实只是为了说明一件事：对问题实例的一般编码不会对问题是否是多项式时间可解产生影响。但是需要理解，选择特殊的编码方式是会对问题求解产生影响的，比如上述的一元编码。

上述的一些定义和证明可能不太好理解，举一个例子：用二进制和三进制编码同一个问题，易知，二进制和三进制可以实现在多项式时间内相互转换（这个转换函数就可以看成上面定义中的 $f_{12}$ 和 $f_{21}$ ，那么其实二进制编码和三进制编码就是多项式相关的）。用二进制解一个问题，假如能在多项式时间内求解的话，那么用三进制求解这个问题，我们可以先把三进制转换为二进制（花费多项式时间），然后用二进制的多项式时间求解，那么我们使用三进制编码求解的总体时间还是多项式时间的。反之，假如三进制编码求解是多项式时间的，那么也可证明二进制编码求解是多项式时间的。

形式语言体系

关注判定问题的好处在于使得形式语言理论的使用变得容易。形式语言的相关定义：

字母表 $\Sigma$ ：符号的有限集合。
语言 $L$ ：由字母表中的符号组成的串的任意集合。使用 $\epsilon$ 表示空串。
$\Sigma^*$ ： $\Sigma$ 上所有语言的集合。

语言的形成过程，以及相关运算这部分可以参考编译原理中的相关知识，此处略。

从语言的角度，任何判定问题Q的实例集即集合 $\Sigma^*$ ，其中 $\Sigma\in\{0,1\}$ 。

另一方面，因为问题Q完全是由解为1（是）的问题实例来描述的，因而可以把Q看做是定义在 $\Sigma=\{0,1\}$ 的一个语言L，其中：
$L=\{x\in\Sigma^*:Q(x)=1\}$
例如，与最短路径判定问题PATH对应的语言为
$PATH=\{<G,u,v,k>:G=(V,E)是一个无向图,u,v\in V,k\geq 0是一个整数， \\即G中从u到v存在一条长度至多为k的路径\}$
形式语言体系可以用来表示判定问题与求解这些问题的算法之间的关系。如果对给定输入 $x$ ，算法输出 $A (x) = 1$ ，我们说算法A接受串 $x\in\{0,1\}^*$ 。被算法A接受的语言是串的集合 $L=\{x\in\{0,1\}^*:A(x)=1\}$ ，即为算法所接受的串的集合。如果 $A (X) = 0$ ，则算法A拒绝串 $x$ 。

接受语言与判定语言的区别：

接受一个语言：存在某个常数 $k$ ，使得对任意长度为n的串 $x\in L$ ，算法A在时间 $O(n^k)$ 内接受 $x$ ，则语言L在多项式时间内被算法A接受。
判定一个语言：存在某个常数 $k$ ，使得对任意长度为n的串 $x\in \{0,1\}$ ，算法A在时间 $O(n^k)$ 内判定 $x\in L$ ，则语言L在多项式时间内被算法A接受。