一、概述
特征工程是机器学习工作流程中不可或缺的一环，它将原始数据转化为模型可理解的形式。数据和特征的质量决定了机器学习的上限，而模型和算法则是逼近这个上限的手段。因此，特征工程的重要性不言而喻。其主要工作涉及特征的采集、预处理、选择以及降维等处理。特征工程是数据分析中最耗费时间和精力的阶段。
1. 特征（Feature)
特征是指从原始数据中提取出的有用信息，用于描述样本的属性。特征可以是数值型的，如身高、体重等，也可以是分类型的，如性别、颜色等。特征通常是用向量或矩阵的形式表示，作为机器学习模型的输入。在特征工程中，我们会对原始数据进行预处理、特征选择、特征提取等操作，以获得更加有用的特征，提高模型的精度和泛化能力。
2. 特征工程（Feature Engineering）
特征工程是指在机器学习中，对原始数据进行预处理、特征选择、特征提取等操作，以获得更加有用的特征，提高模型的精度和泛化能力的过程。特征工程旨在将原始数据转换为机器学习算法能够理解和处理的形式，为模型提供更加有用的信息。在特征工程中，我们可以对原始数据进行清洗、处理、归一化、缩放等操作，以去除噪声和异常值，提高数据的质量；同时，我们也可以通过特征选择、特征提取等技术，从原始数据中提取出更加有用的特征，以提高模型的精度和泛化能力。
3. 特征工程的意义
提高数据质量：特征工程可以对原始数据进行清洗、处理、归一化、缩放等操作，去除噪声和异常值，提高数据的质量。
提高模型性能：特征工程可以通过特征选择、特征提取等技术，从原始数据中提取出更加有用的特征，提高模型的精度和泛化能力。
减少过拟合：特征工程可以通过降维等技术，减少特征的数量，避免模型出现过拟合的问题。
降低计算成本：特征工程可以通过降维等技术，减少模型的复杂度，降低计算成本。
总之，特征工程是机器学习过程中非常重要的一环，其意义在于提高数据质量、提高模型性能、减少过拟合、降低计算成本等方面。特征工程的好坏直接影响着机器学习算法的性能和表现。
二、特征工程数据预处理
1 离散化（静态连续变量）
离散化是数据预处理中的一项重要技术，它是将连续型数据转换为离散型数据的过程。在机器学习中，离散化的目的是为了将连续型数据转换为可以处理的离散型数据，从而方便数据分析和建模。
离散化的方法包括分箱(等宽离散化、等频离散化)和聚类算法（K-means离散化）等。其中，等宽离散化是将数据按照固定的区间宽度进行划分，例如将数据按照每个区间宽度为10进行离散化；等频离散化是将数据按照相同数量的数据点划分为每个区间，例如将数据划分为10个区间，每个区间包含相同数量的数据点；K-means离散化是利用聚类算法将数据划分为K个簇，每个簇代表一个离散化的值。
离散化可以减少数据的复杂度，提高数据的可解释性和可处理性。例如，在某个房价预测模型中，将房屋面积进行离散化，可以将连续的面积数据划分为几个离散的区间，从而方便建立预测模型。
1.1 分箱
- 等宽离散法
# JuPyter写法
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import KBinsDiscretizer
# 加载iris数据集
iris = load_iris()
# 将数据集转换为DataFrame格式
df = sns.load_dataset('iris')
# 对花瓣长度进行等频分区
est = KBinsDiscretizer(n_bins=4, encode='ordinal', strategy='uniform')
est.fit(df[['sepal_length']])
df['petal_length_group'] = est.transform(df[['petal_length']])
print(df)
bin_edge = est.bin_edges_[0]
print(bin_edge)
# 绘图
sns.distplot(df['sepal_length'], kde=True)
for edge in bin_edge: # uniform bins
line = plt.axvline(edge, color='b')
plt.xlabel('Petal Length Group')
plt.ylabel('Petal Width')
plt.title('Petal Width by Petal Length Group')
plt.show()结果展示：
sepal_length sepal_width ... species petal_length_group
0 5.1 3.5 ... setosa 0.0
1 4.9 3.0 ... setosa 0.0
2 4.7 3.2 ... setosa 0.0
3 4.6 3.1 ... setosa 0.0
4 5.0 3.6 ... setosa 0.0
.. ... ... ... ... ...
145 6.7 3.0 ... virginica 1.0
146 6.3 2.5 ... virginica 0.0
147 6.5 3.0 ... virginica 1.0
148 6.2 3.4 ... virginica 1.0
149 5.9 3.0 ... virginica 0.0
[150 rows x 6 columns]
[4.3 5.2 6.1 7. 7.9]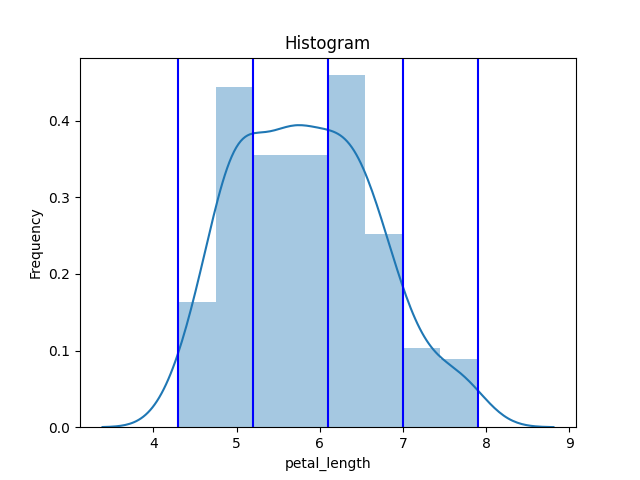
1.2. 等频离散法
# JuPyter写法
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import KBinsDiscretizer
# 加载iris数据集
iris = load_iris()
# 将数据集转换为DataFrame格式
df = sns.load_dataset('iris')
# 对花瓣长度进行等频分区
est = KBinsDiscretizer(n_bins=4, encode='ordinal', strategy='uniform')
est.fit(df[['sepal_length']])
df['petal_length_group'] = est.transform(df[['petal_length']])
print(df)
bin_edge = est.bin_edges_[0]
print(bin_edge)
# 绘图
sns.distplot(df['sepal_length'], kde=True)
for edge in bin_edge: # uniform bins
line = plt.axvline(edge, color='b')
plt.xlabel('Petal Length Group')
plt.ylabel('Petal Width')
plt.title('Petal Width by Petal Length Group')
plt.show()结果展示
sepal_length sepal_width ... species petal_length_group
0 5.1 3.5 ... setosa 0.0
1 4.9 3.0 ... setosa 0.0
2 4.7 3.2 ... setosa 0.0
3 4.6 3.1 ... setosa 0.0
4 5.0 3.6 ... setosa 0.0
.. ... ... ... ... ...
145 6.7 3.0 ... virginica 1.0
146 6.3 2.5 ... virginica 0.0
147 6.5 3.0 ... virginica 1.0
148 6.2 3.4 ... virginica 1.0
149 5.9 3.0 ... virginica 1.0
[150 rows x 6 columns]
[4.3 5.1 5.8 6.4 7.9]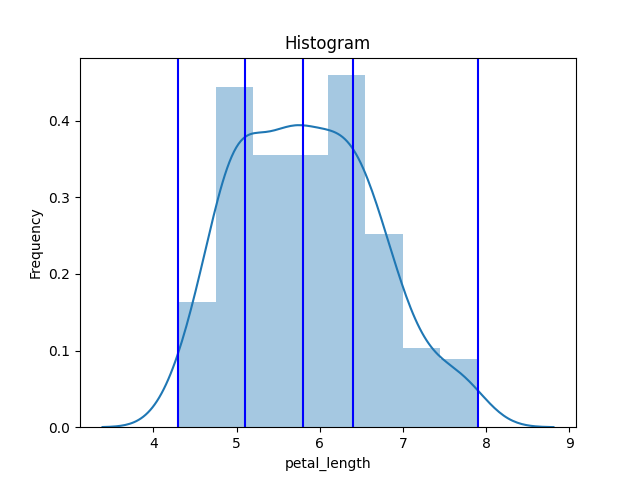
1.2 聚类算法
from sklearn.cluster import KMeans
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt
# 加载iris数据集
iris = load_iris()
X = iris.data
# 初始化聚类模型
kmeans = KMeans(n_clusters=3, random_state=0)
# 训练模型
kmeans.fit(X)
# 获取聚类结果
y_kmeans = kmeans.predict(X)
# 绘制聚类结果散点图
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=50, cmap='viridis')
centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c='black', s=200, alpha=0.5)
plt.xlabel('Sepal Length')
plt.ylabel('Sepal Width')
plt.title('KMeans Clustering')
plt.show()结果展示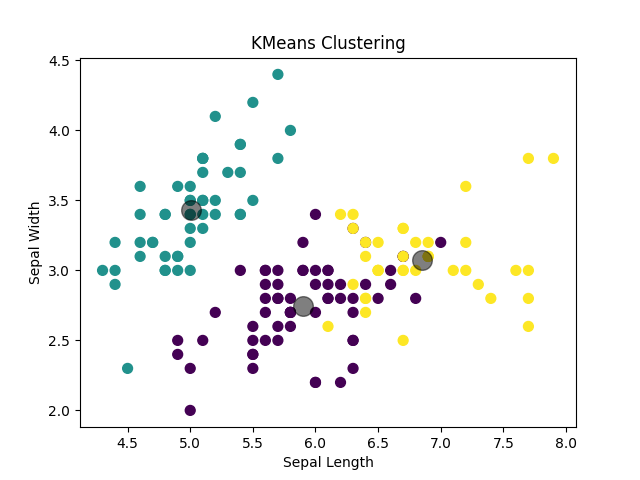 
2. 缩放（静态连续变量）
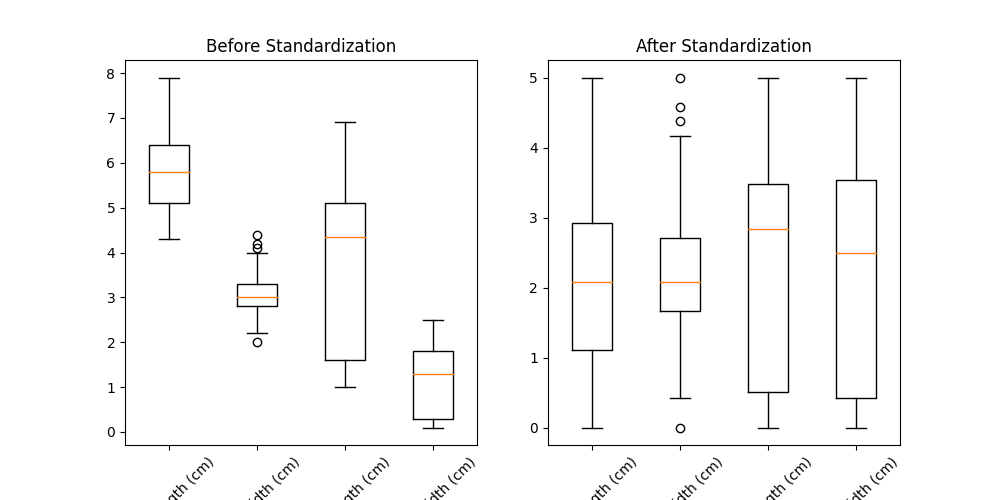
2.1. 标准化（Standardization）
标准化：
X` = \frac {x - mean(x)}{δ}x为变量，mean(x)为均值，δ为x的标准差。将特征缩放到均值为0，方差为1的标准正态分布中，使得特征具有相似的尺度，从而避免特征值的尺度差异对模型的影响
from sklearn.preprocessing import StandardScaler
import numpy as np
from sklearn.datasets import load_iris
# 加载iris数据集
iris = load_iris()
# 获取特征矩阵
X = iris.data
# 创建标准化器对象
scaler = StandardScaler()
# 对特征矩阵进行标准化
X_std = scaler.fit_transform(X)
# 绘制标准化前后的数据箱线图
fig, ax = plt.subplots(1, 2, figsize=(10, 5))
ax[0].boxplot(X)
ax[0].set_xticklabels(iris.feature_names, rotation=45)
ax[0].set_title('Before Standardization')
ax[1].boxplot(X_std)
ax[1].set_xticklabels(iris.feature_names, rotation=45)
ax[1].set_title('After Standardization')
plt.show()标准化结果前后对比图 
2.2. 最大最小值缩放（MinMax Scaling）
归一化：
x' = \frac{x - min(x)}{max(x) - min(x)}*(b-a)+a最大最小值缩放是一种常用的数据标准化方法，它将数据缩放到一个指定的范围之内，通常是[0, 1]或[-1, 1]。该方法可以使得不同特征之间的数据具有可比性，避免了某些特征因为数据范围不同而对模型产生影响。归一化（Normalization） 将特征缩放到0和1之间，适用于特征值范围较小的情况,是最大最小值缩放的一个特例，对应b=1和a=0的情况，这里另外介绍。
from sklearn.datasets import load_iris
from sklearn.preprocessing import MinMaxScaler
import matplotlib.pyplot as plt
# 加载数据集
iris = load_iris()
X = iris.data
y = iris.target
# 最大最小值缩放
scaler = MinMaxScaler(feature_range=(0, 5))
X_scaled = scaler.fit_transform(X)
# 绘制图形
plt.figure(figsize=(10, 6))
plt.scatter(X[:, 0], X[:, 1], c=y)
plt.title("Original Data", fontsize=16)
plt.xlabel("Sepal Length", fontsize=14)
plt.ylabel("Sepal Width", fontsize=14)
plt.show()
plt.figure(figsize=(10, 6))
plt.scatter(X_scaled[:, 0], X_scaled[:, 1], c=y)
plt.title("Scaled Data", fontsize=16)
plt.xlabel("Sepal Length (scaled)", fontsize=14)
plt.ylabel("Sepal Width (scaled)", fontsize=14)
plt.show()结果展示:
[[1.11111111 3.125 0.33898305 0.20833333]
[0.83333333 2.08333333 0.33898305 0.20833333]
[0.55555556 2.5 0.25423729 0.20833333]
[0.41666667 2.29166667 0.42372881 0.20833333]
[0.97222222 3.33333333 0.33898305 0.20833333]
[1.52777778 3.95833333 0.59322034 0.625 ]
...]
从图中可以看出，经过最大最小值缩放后，数据被缩放到了 0 到 5 的范围内，并且不同特征之间的数据具有可比性
2.3 幂次变换
- 对数转换（Log Transformation）
将特征进行对数转换，适用于特征值范围较大，但分布不均匀的情况.对数转换可以将数据的范围缩小，使得数据更加平滑，更容易处理。对数转换可以减小离群值的影响，使得数据更加符合正态分布，便于进行统计分析和建模。对数转换: y=log(X)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston
# 加载波士顿房价数据集
boston = load_boston()
# 取出数据集中的房价数据
y = boston.target
# 对房价数据进行对数转换
y_log = np.log(y)
print(y_log)
# 绘制对数转换前后的房价数据分布图
fig, ax = plt.subplots(1, 2, figsize=(10, 5))
ax[0].hist(y, bins=50)
ax[0].set_title('Original Data')
ax[1].hist(y_log, bins=50)
ax[1].set_title('Log Transformed Data')
plt.show()结果展示：
[3.17805383 3.07269331 3.54673969 3.5085559 3.58905912 3.35689712
3.13113691 3.29953373 2.80336038 2.93916192 2.7080502 2.93916192
3.07731226 3.0155349 2.90142159 2.99071973 3.13983262 2.86220088
3.0056826 2.90142159 2.61006979 2.97552957 2.72129543 2.67414865
2.74727091 2.63188884 2.8094027 2.69462718 2.91235066 3.04452244 ...]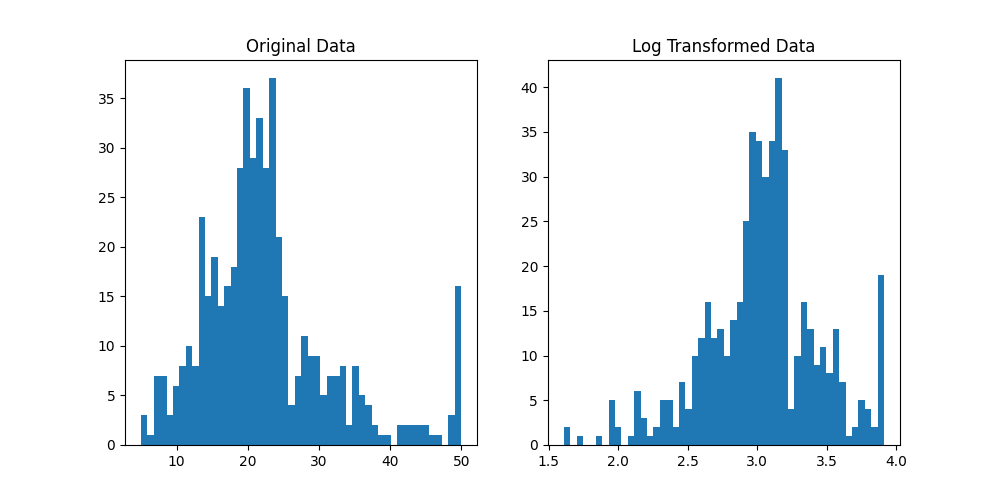
从上图可以看出，经过对数转换后，房价数据更加符合正态分布，更容易进行建模和分析。
2. Box-Cox变换
Box-Cox变换: y(λ) = \begin{cases}
{\frac {y^λ-1} λ} &\text{if \space} λ \space {=}\mathllap{/\,}\space 0 \\
ln(y) &\text{if } \space λ = 0
\end{cases}Box-Cox变换是一种常用的数据变换方法，用于将数据转换为正态分布或近似正态分布.意义在于，许多机器学习算法都假设数据服从正态分布或近似正态分布。如果数据不满足这个假设，可能会影响模型的性能。通过Box-Cox变换，可以将数据转换为正态分布或近似正态分布，从而提高模型的预测能力。变换只适用于正数。
from sklearn.datasets import load_iris
from scipy import stats
import matplotlib.pyplot as plt
# 加载数据集
iris = load_iris()
X = iris.data[:, :2] # 取前两个特征
y = iris.target
# 对数据进行Box-Cox变换
X_bc, lmbda = stats.boxcox(X.reshape(-1)) # 将二维数组转换为一维数组并进行变换
# 绘制变换前后的直方图
fig, ax = plt.subplots(1, 2, figsize=(10, 5))
ax[0].hist(X.reshape(-1), bins=20)
ax[0].set_title('Original Data')
ax[1].hist(X_bc, bins=20)
ax[1].set_title('Box-Cox Transformed Data')
plt.show()结果展示：
[1.65256141 1.2665211 1.61141969 1.1091834 1.5685937 1.17500487
1.54650446 1.14261581 1.63219269 1.29532005 1.71139318 1.37722443
1.54650446 1.23690202 1.63219269 1.23690202 1.50087381 1.07463754
1.61141969 1.14261581 1.71139318 1.32334344 1.59022588 1.23690202
1.59022588 1.1091834 1.47728844 1.1091834 1.78502653 ...] 0.01740561324159318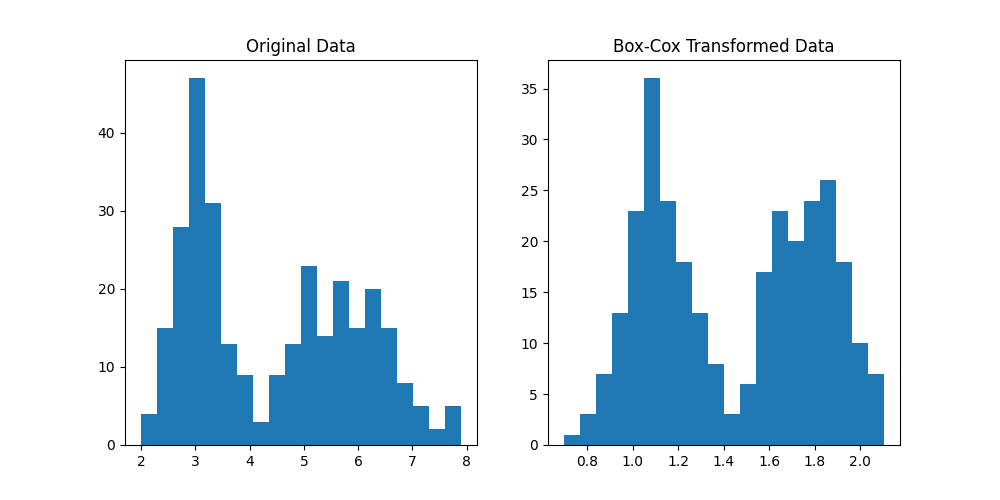
- Yeo-Johnson 变换
Yeo-Johnson 变换: x_i^{(λ)} = \begin{cases}
\frac {({(x_i+1)}^λ-1)} λ, &\text{if } λ \space {=}\mathllap{/\,}\space 0,x_i \geqslant 0\\
ln(x_i+1), &\text{if } λ = 0, x_i \geqslant 0\\
\frac {-((-x_i+1)^{2-λ}-1)} {2-λ}, &\text{if } λ \space{=}\mathllap{/\,}\space 2, x_i <0\\
-ln(-x_i+1), &\text{if } λ = 2,x_i <0
\end{cases}其中， λ是一个可调参数，可以通过最小化残差平方和来确定。Yeo-Johnson变换可以将数据从任意分布转换为正态分布，从而提高机器学习算法的准确性。 Yeo-Johnson变换是一种数据预处理技术，用于对数据进行正态化处理。它是Box-Cox变换的一种变体，它可以处理包括负数在内的所有实数。
from sklearn.datasets import load_boston
from sklearn.preprocessing import PowerTransformer
import matplotlib.pyplot as plt
# 加载数据集
boston = load_boston()
X = boston.data
y = boston.target
# 对数据进行Yeo-Johnson变换
pt = PowerTransformer(method='yeo-johnson')
X_trans = pt.fit_transform(X)
# 绘制数据分布图
fig, axs = plt.subplots(1, 2, figsize=(6, 6))
axs[0].hist(X[:, 0], bins=50)
axs[0].set_title('Original data')
axs[1].hist(X_trans[:, 0], bins=50)
axs[1].set_title('Transformed data')
plt.tight_layout()
plt.show()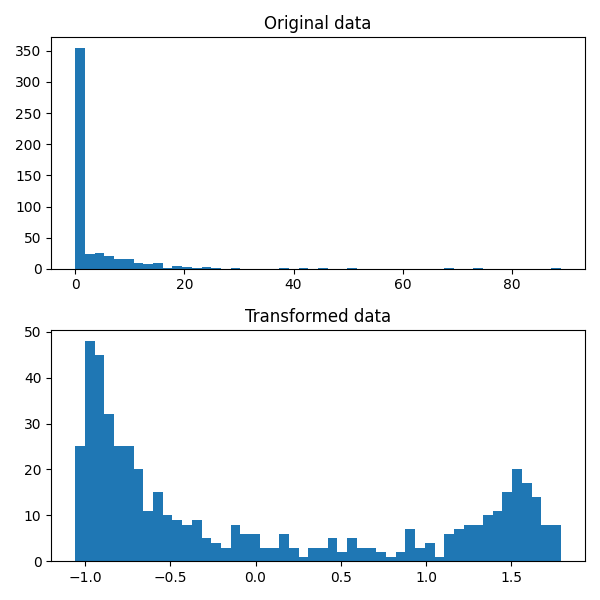
从图中可以看出，经过Yeo-Johnson变换后，数据分布更加接近正态分布。
3. 正则化（静态连续变量）
正则化是一种用于控制模型复杂度的技术，可以避免过拟合问题,并提高模型的泛化能力。在机器学习中，正则化通常通过在损失函数中添加惩罚项来实现，惩罚项会惩罚模型中的大型权重。常用的正则化方法有L1正则化和L2正则化。
- L1正则化
L1正则化: J(θ) = \frac {1} {m} \sum_{i=1}^m L(\text {\^{y}}_i,y_i)+ λ\sum_{j=1}^n|θ_j|其中，θ是模型的权重，L是损失函数，λ是正则化参数，n是权重的数量。
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.linear_model import Lasso
# 加载数据集
X, y = datasets.load_diabetes(return_X_y=True)
# 创建Lasso回归模型
lasso = Lasso(alpha=0.1)
# 拟合模型
lasso.fit(X, y)
# 输出系数
print(lasso.coef_)
# 绘制系数图
plt.plot(lasso.coef_, color='r', label='Lasso coefficients')
plt.xlabel('Features')
plt.ylabel('Coefficients')
plt.title('Lasso coefficients')
plt.legend()
plt.show()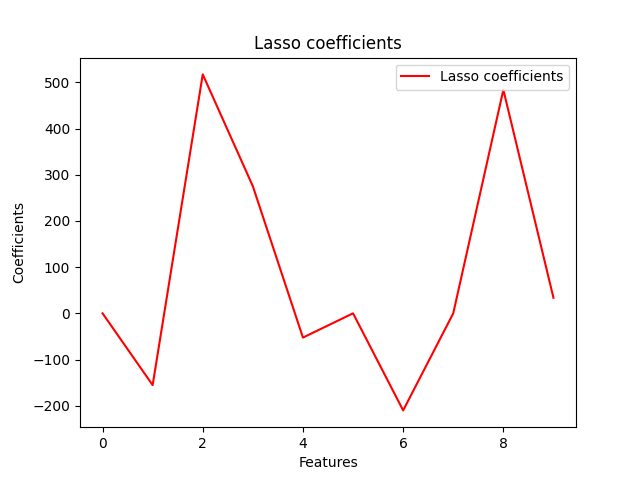
这将显示出一个系数图，其中每个系数都与其对应的特征相关联。我们可以看到，许多系数被缩小到零，这意味着它们对模型的预测没有贡献。 2. L2正则化
L2正则化: J(θ) = \frac {1} {m} \sum_{i=1}^m L(\text {\^{y}}_i,y_i)+ \frac λ 2\sum_{j=1}^n θ_j^2其中，θ是模型的权重，L是损失函数，λ是正则化参数，n是权重的数量。
from sklearn.datasets import load_boston
from sklearn.linear_model import Ridge
import matplotlib.pyplot as plt
# 加载数据集
boston = load_boston()
X = boston.data
y = boston.target
# 使用Ridge模型进行L2正则化
ridge = Ridge(alpha=0.1)
ridge.fit(X, y)
coef = ridge.coef_
# 绘制权重系数图
plt.plot(range(len(coef)), coef)
plt.title('Ridge coefficients')
plt.xlabel('Feature index')
plt.ylabel('Coefficient value')
plt.show()结果展示：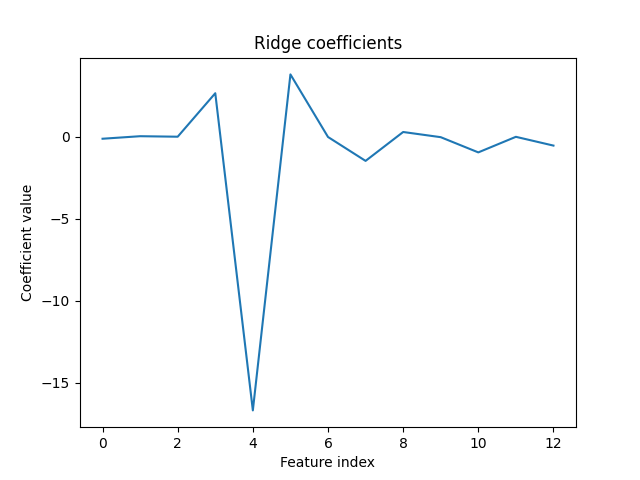 
从图中可以看出，L2正则化可以将模型的权重系数缩小，避免过拟合问题。
4. 缺失值的估算（静态连续变量）
在实际操作中，数据集中可能缺少值。然而，这种稀疏的数据集与大多数 scikit 学习模型不兼容，这些模型假设所有特征都是数值的，而没有丢失值。所以在应用 scikit 学习模型之前，我们需要估算缺失的值。
4.1. 删除法（Deletion）
删除法是最简单的缺失值估算方法，直接将带有缺失值的样本或特征删除。但是，如果缺失值的比例较高，删除法会导致样本量过少或特征过少，从而影响模型的准确性。
4.2. 插值法（Imputation）
插值法是通过已有的数据来估算缺失值。插值法包括以下几种常用方法：
- 单变量特征插补
假设第x列中有缺失值，那么我们将用常数或第x 列的统计数据（平均值、中值或模式）对其进行估算。
from sklearn.impute import SimpleImputer
import numpy as np
# 构造一个有缺失值的二维数组
X = np.array([[1, 2, 3], [4, np.nan, 6], [7, 8, np.nan], [10, 11, 12]])
# 创建一个SimpleImputer对象，使用均值插值
imputer = SimpleImputer(strategy='mean')
# 对X进行插值处理
X_imputed = imputer.fit_transform(X)
# 输出插值后的结果
print(X_imputed)结果展示：
[[ 1. 2. 3. ]
[ 4. 7. 6. ]
[ 7. 8. 7. ]
[10. 11. 12. ]]可以看到，原来X数组中的缺失值被均值插值处理后，得到了一个完整的二维数组。 2. 多元特征插补
多元特征插补利用整个数据集的信息来估计和插补缺失值。在 scikit-learn 中，它以循环迭代的方式实现。 现在我们将使用sklearn库中的IterativeImputer类来插补缺失值。这个类使用回归模型来预测缺失值。
from sklearn.datasets import load_iris
import pandas as pd
import numpy as np
from sklearn.experimental import enable_iterative_imputer
from sklearn.impute import IterativeImputer
iris = load_iris()
df = pd.DataFrame(data= np.c_[iris['data'], iris['target']],
columns= iris['feature_names'] + ['target'])
# 创建缺失项
df_missing = df.copy()
df_missing.iloc[2:4, 1] = np.nan
df_missing.iloc[3:6, 2] = np.nan
df_missing.iloc[5:7, 3] = np.nan
df_missing.iloc[7:9, 0] = np.nan
df_missing.iloc[8:10, 1] = np.nan
df_missing.iloc[10:13, 2] = np.nan
df_missing.iloc[11:14, 3] = np.nan
print(df_missing)
# 创建实例
imputer = IterativeImputer()
imputer.fit(df_missing)
df_imputed = pd.DataFrame(data=imputer.transform(df_missing), columns=df_missing.columns)
print(df_imputed)缺失值结果展示：
sepal length (cm) sepal width (cm) petal length (cm) petal width (cm) target
0 5.1 3.5 1.4 0.2 0.0
1 4.9 3.0 1.4 0.2 0.0
2 4.7 NaN 1.3 0.2 0.0
3 4.6 NaN NaN 0.2 0.0
4 5.0 3.6 NaN 0.2 0.0
5 5.4 3.9 1.7 NaN 0.0
6 4.6 3.4 1.4 0.3 0.0
7 NaN 3.4 1.5 0.2 0.0
8 NaN NaN 1.4 0.2 0.0
9 4.9 3.1 NaN 0.1 0.0
10 5.4 3.7 NaN NaN 0.0
11 4.8 3.4 1.6 NaN 0.0
12 4.8 3.0 NaN NaN 0.0
13 4.3 3.0 NaN NaN 0.0
14 5.8 4.0 1.2 0.2 0.0
...补全结果展示：
sepal length (cm) sepal width (cm) petal length (cm) petal width (cm) target
0 5.100000 3.500000 1.400000 0.200000 0.0
1 4.900000 3.000000 1.400000 0.200000 0.0
2 4.700000 3.283147 1.300000 0.200000 0.0
3 4.600000 3.238815 1.213727 0.200000 0.0
4 5.000000 3.600000 1.222952 0.200000 0.0
5 5.400000 3.900000 1.700000 0.353042 0.0
6 4.600000 3.400000 1.400000 0.300000 0.0
7 5.007057 3.400000 1.500000 0.200000 0.0
8 4.982975 3.307063 1.400000 0.200000 0.0
9 4.900000 3.100000 1.213727 0.100000 0.0
10 5.400000 3.700000 1.223548 0.240023 0.0
11 4.800000 3.400000 1.600000 0.341056 0.0
12 4.800000 3.000000 1.215897 0.227493 0.0
13 4.300000 3.000000 1.207741 0.198455 0.0
14 5.800000 4.000000 1.200000 0.200000 0.0
...- 标记估算值（Prediction）
标记估算值是机器学习中的一个重要概念，指的是模型对未知数据的预测值。在机器学习中，通常将数据集分为训练集和测试集，使用训练集训练模型，然后使用测试集来评估模型的性能，其中就需要使用模型对测试集的数据进行预测，得到标记估算值。
下面是一个使用sklearn中的波士顿房价数据集进行线性回归，并计算标记估算值的示例代码：
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
# 加载数据集
boston = load_boston()
X = boston.data
y = boston.target
# 将数据集分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 使用线性回归模型进行训练
lr = LinearRegression()
lr.fit(X_train, y_train)
# 对测试集的数据进行预测，得到标记估算值
y_pred = lr.predict(X_test)
# 输出前10个标记估算值
print(y_pred[:10])结果展示：
[28.99672362 36.02556534 14.81694405 25.03197915 18.76987992
23.25442939 17.66253818 14.34119 23.01352664 20.63245538]可以看出，得到了测试集上的标记估算值，用于评估模型的性能。
5. 特征变换（静态连续变量）
- 多项式变换（Polynomial Transformation）
多项式变换是机器学习中的一种特征工程方法，可以将原始特征进行组合，生成新的特征，从而提高模型的表现。在sklearn中，可以使用PolynomialFeatures类来进行多项式变换。
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PolynomialFeatures
# 加载数据集
boston = load_boston()
X = boston.data
y = boston.target
# 将数据集分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 进行多项式变换
poly = PolynomialFeatures(degree=2)
X_train_poly = poly.fit_transform(X_train)
X_test_poly = poly.transform(X_test)
# 使用线性回归模型进行训练
lr = LinearRegression()
lr.fit(X_train_poly, y_train)
# 在测试集上进行预测并评估模型性能
score = lr.score(X_test_poly, y_test)
print('R^2 score:', score)结果展示:
R^2 score: 0.7258515818230033可以看出，使用多项式变换后，线性回归模型在测试集上的表现得到了明显提升，R^2分数达到了0.72左右。
- 自定义变换（Custom Transformer）
自定义变换是一种常见的特征工程方法，可以根据数据的特点，自定义一些变换操作，从而提高模型的表现。在sklearn中，可以通过自定义Transformer类来实现自定义变换。
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.base import BaseEstimator, TransformerMixin
# 定义自定义Transformer类
class CustomTransformer(BaseEstimator, TransformerMixin):
def __init__(self):
pass
def fit(self, X, y=None):
return self
def transform(self, X):
# 对数据进行自定义变换
X_new = X[:, [0, 5, 6, 7]]
X_new[:, 0] = X_new[:, 0] ** 2
X_new[:, 1] = X_new[:, 1] / X_new[:, 2]
return X_new
# 加载数据集
boston = load_boston()
X = boston.data
y = boston.target
# 将数据集分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 进行自定义变换
ct = CustomTransformer()
X_train_new = ct.fit_transform(X_train)
X_test_new = ct.transform(X_test)
# 使用线性回归模型进行训练
lr = LinearRegression()
lr.fit(X_train_new, y_train)
# 在测试集上进行预测并评估模型性能
score = lr.score(X_test_new, y_test)
print('R^2 score:', score)结果展示：
R^2 score: 0.6027146214638019可以看出，使用自定义变换后，线性回归模型在测试集上的表现得到了一定提升，R^2分数达到了0.60左右。
本文由博客一文多发平台 OpenWrite 发布！
