t0.解题五部曲
1.基础入门题目
- - 1.509. 斐波那契数
  - 2.70. 爬楼梯
  - 3.746. 使用最小花费爬楼梯
  - 4.62. 不同路径
  - 5.63. 不同路径 II
  - 6.343. 整数拆分
  - 7.96. 不同的二叉搜索树
2.背包问题
- 1.01背包（二维数组实现）
- 2.01背包（滚动数组实现）
- - 1.416. 分割等和子集
  - 2.1049. 最后一块石头的重量 II
  - *3.494. 目标和
  - 4.474. 一和零
- 2.完全背包
- - 1.518. 零钱兑换 II
  - 2.377. 组合总和 Ⅳ
  - 3.322. 零钱兑换
  - 4.279. 完全平方数
  - *5.139. 单词拆分
3.打家劫舍
- - 1.198. 打家劫舍
  - 2.213. 打家劫舍 II
  - 3.337. 打家劫舍 III
4.股票问题
- - 1.121. 买卖股票的最佳时机
  - 2.122. 买卖股票的最佳时机 II
  - 3.123. 买卖股票的最佳时机 III
  - 4.188. 买卖股票的最佳时机 IV
  - 5.309. 最佳买卖股票时机含冷冻期
  - 6.714. 买卖股票的最佳时机含手续费
5.子序列问题
- 1.子序列（不连续）
- - 1.300. 最长递增子序列
  - 2.1143. 最长公共子序列
  - 3.1035. 不相交的线
- 2.子序列（连续）
- - 1.674. 最长连续递增序列
  - *2.718. 最长重复子数组
  - 3.53. 最大子数组和
- 3.编辑距离
- - 1.392. 判断子序列
  - 2.115. 不同的子序列
  - 3.583. 两个字符串的删除操作
  - 4.72. 编辑距离
- 4.回文
- - 1.647. 回文子串
  - 2.516. 最长回文子序列

t0.解题五部曲

1. 确定dp数组（dp table）以及下标的含义
2. 确定递推公式
3. dp数组如何初始化
4. 确定遍历顺序
5. 举例推导dp数组

1.基础入门题目

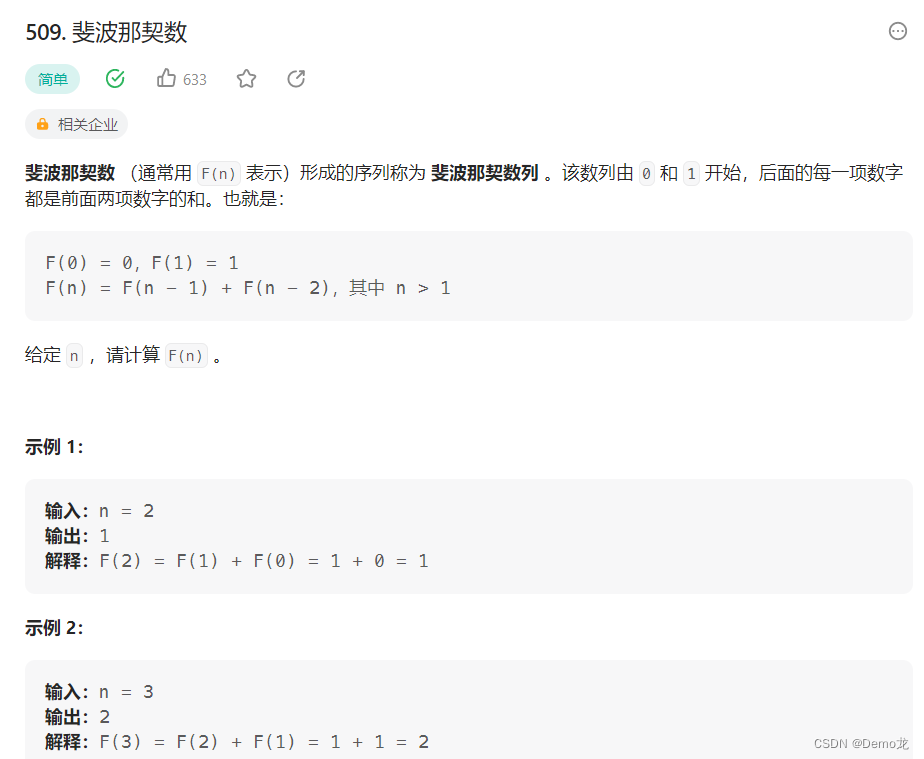
1.509. 斐波那契数

链接: 509. 斐波那契数
在这里插入图片描述

class Solution {
    public int fib(int n) {
        if(n<=1){
            return n;
        }
        int arr[]=new int[n+1];
        arr[0]=1;
        arr[1]=1;
        for(int i=2;i<=n;i++){
            arr[i]=arr[i-2]+arr[i-1];
        }
        return arr[n-1];
    }
}

class Solution {
    public int fib(int n) {
        if(n<=1){
            return n;
        }
        int arr0=0;
        int arr1=1;
        for(int i=2;i<=n;i++){
            int sum=arr0+arr1;
            arr0=arr1;
            arr1=sum;
        }
        return arr1;
    }
}

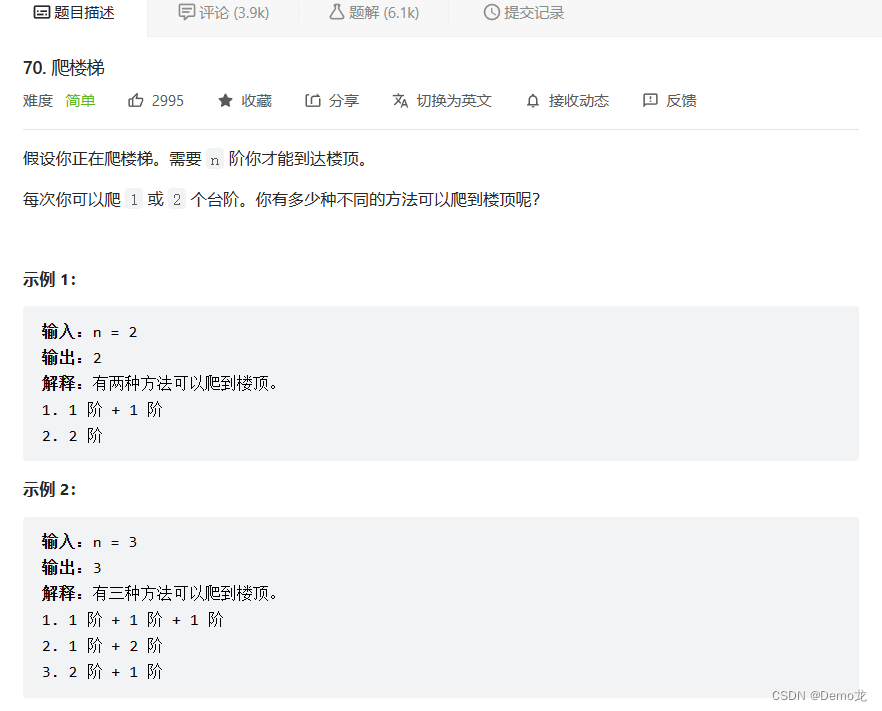
2.70. 爬楼梯

链接: 70. 爬楼梯
在这里插入图片描述

class Solution {
    public int climbStairs(int n) {
        if(n<=2){
            return n;
        }
        int dp[]=new int[n+1];
        dp[1]=1;
        dp[2]=2;
        for(int i=3;i<=n;i++){
            dp[i]=dp[i-1]+dp[i-2];
        }
        return dp[n];
    }
}

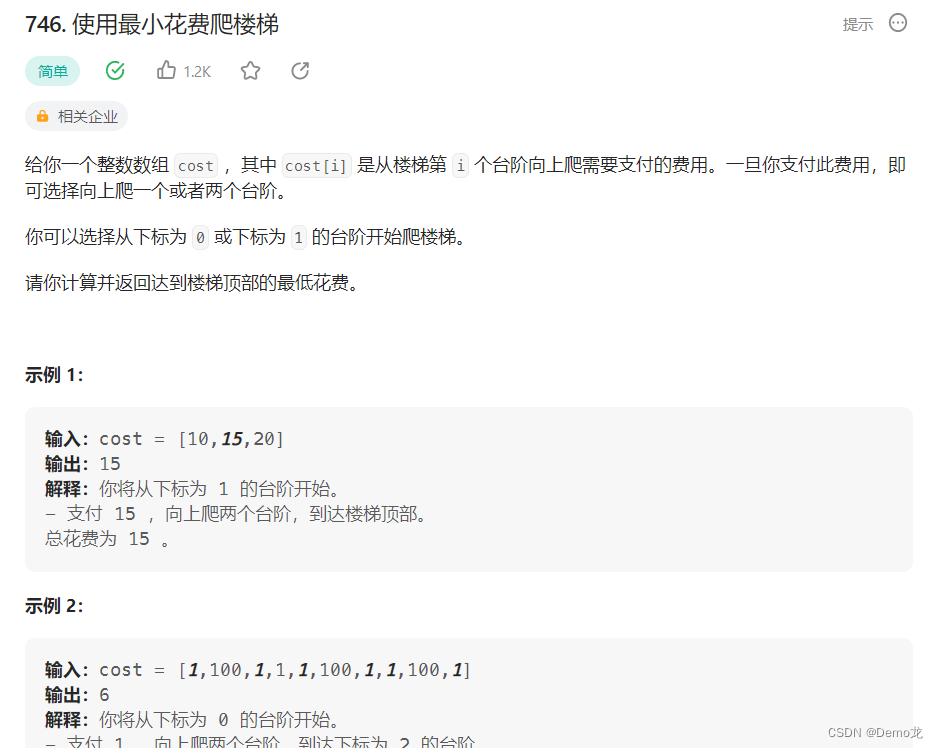
3.746. 使用最小花费爬楼梯

链接: 746. 使用最小花费爬楼梯
在这里插入图片描述

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int n=cost.length;
        int dp[]=new int [n+1];
        dp[0]=0;
        dp[1]=0;
        for(int i=2;i<=n;i++){
            dp[i]=Math.min((dp[i-1]+cost[i-1]),(dp[i-2]+cost[i-2]));
        }
        return dp[n];
    }
}

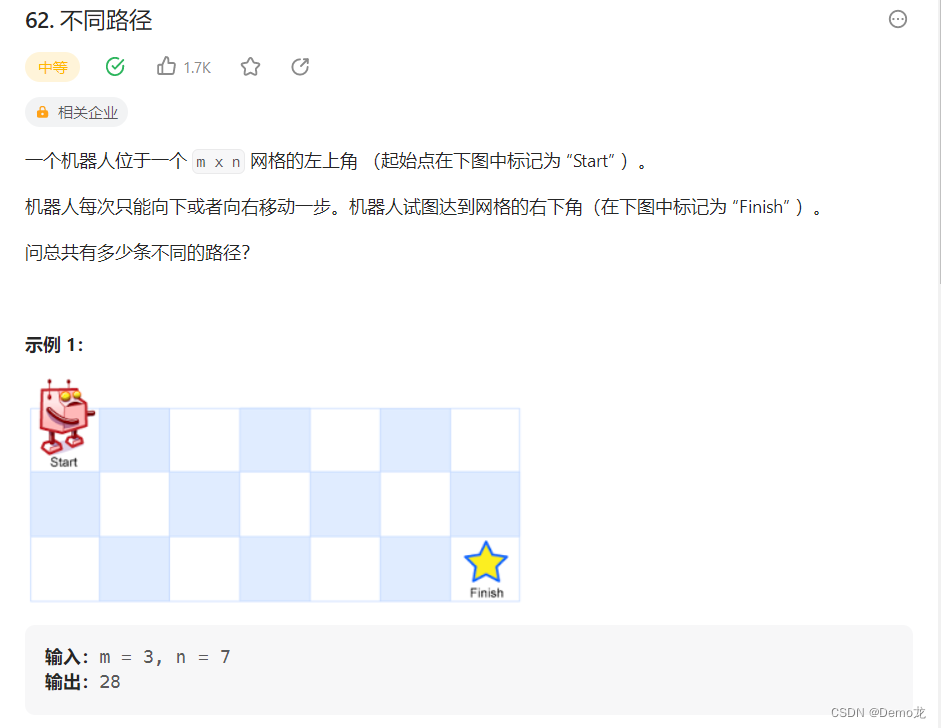
4.62. 不同路径

链接: 62. 不同路径
在这里插入图片描述

class Solution {
    public int uniquePaths(int m, int n) {
        int dp[][]=new int[m][n];
        for(int i=0;i<m;i++){
            dp[i][0]=1;
        }
        for(int i=0;i<n;i++){
            dp[0][i]=1;
        }
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                dp[i][j]=dp[i-1][j]+dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
}

5.63. 不同路径 II

在这里插入图片描述

链接: 63. 不同路径 II

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int m=obstacleGrid.length;
        int n=obstacleGrid[0].length;
        if(obstacleGrid[m-1][n-1]==1||obstacleGrid[0][0]==1){
            return 0;//当start位置和finish位置有障碍时直接返回0
        }
        int dp[][]=new int[m][n];//从start每一个坐标点有多少条不同的路径
        for(int i=0;i<m&&obstacleGrid[i][0]==0;i++){
            dp[i][0]=1;//满足条件初始化第一列，若有障碍后面的dp都为0
        }
        for(int i=0;i<n&&obstacleGrid[0][i]==0;i++){
            dp[0][i]=1;//满足条件初始化第一行，若有障碍后面的dp都为0
        }
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                if(obstacleGrid[i][j]==0){
                    dp[i][j]=dp[i-1][j]+dp[i][j-1];
                }
            }
        }
        return dp[m-1][n-1];
    }
}

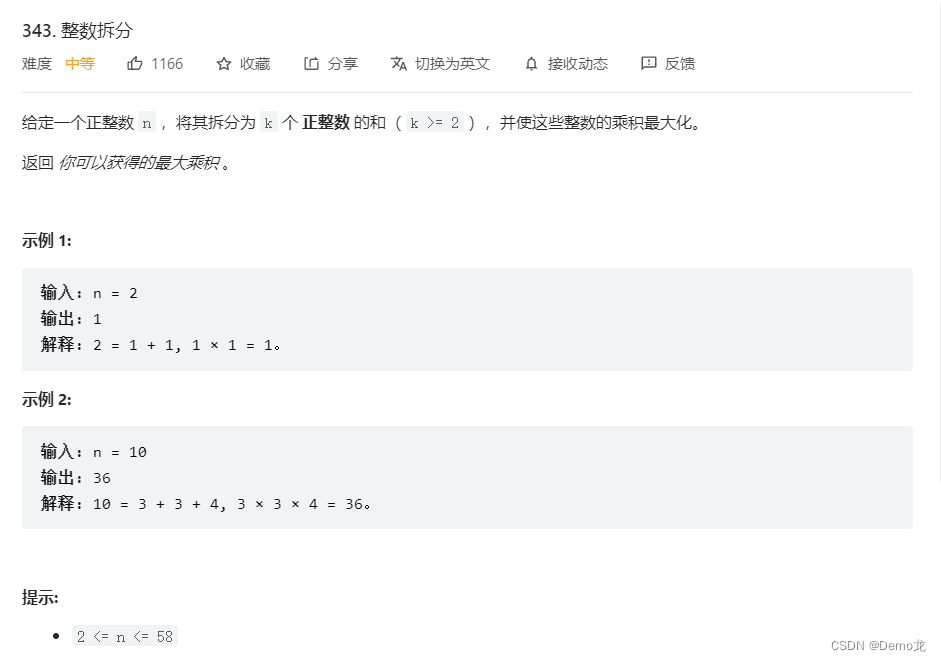
6.343. 整数拆分

链接: 343. 整数拆分
在这里插入图片描述

class Solution {
    public int integerBreak(int n) {
        int dp[]=new int[n+1];
        dp[2]=1;
        for(int i=3;i<=n;i++){

            for(int j=1;j<=i/2;j++){

                dp[i]=Math.max(dp[i],Math.max(j*dp[i-j],j*(i-j)));

            }

        }
        return dp[n];
    }
}

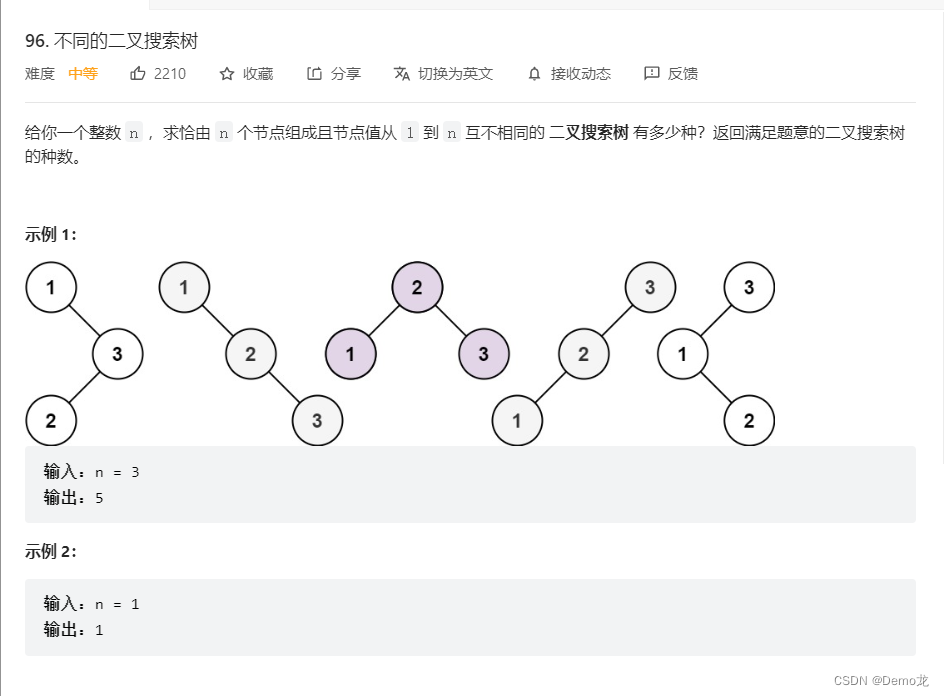
7.96. 不同的二叉搜索树

链接: 96. 不同的二叉搜索树
在这里插入图片描述

class Solution {
    public int numTrees(int n) {
        int dp[]=new int[n+1];
        dp[0]=1;
        for(int i=1;i<=n;i++){
            for(int j=1;j<=i;j++){
                dp[i]+=dp[i-j]*dp[j-1];
            }
        }
        return dp[n];
    }
}

2.背包问题

1.01背包（二维数组实现）

1.dp[i][j]数组含义：dp[i][j] 表⽰从下标为[0-i]的物品⾥任意取，放进容量为j的背包，价值总和最⼤是多少。

2.递推方程：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

01背包问题Java代码

public class Knapsack_problem01 {
    //01背包问题
    public static void main(String[] args) {
        System.out.println("背包最大价值"+knapsack());
    }
    //01背包
    //dp[i][j]数组含义：dp[i][j] 表⽰从下标为[0-i]的物品⾥任意取，
    //放进容量为j的背包，价值总和最⼤是多少。
    public static int knapsack(){
        int wight[]={1,3,4};
        int value[]={15,20,30};
        int bagW=4;
        int [][]dp=new int[wight.length][bagW+1];

        for (int i = bagW; i >= wight[0]; i--) {//初始化dp
            dp[0][i]=value[0];
        }
        //打印初始化后的dp数组
        System.out.println("=====初始化后的dp=====");
        printDP(dp);

//        for(int i=1;i<=bagW;i++){//先遍历背包容量
//            for (int j = 1; j < wight.length; j++){//遍历物品，wight数组的大小就是物品个数
//                if(i-wight[j]>=0)
//                dp[j][i]=Math.max(dp[j-1][i],(dp[j-1][i-wight[j]]+value[j]));
//            }
//        }
        for(int i=1;i<wight.length;i++){//先遍历物品，wight数组的大小就是物品个数
            for (int j = 1; j <= bagW; j++){//遍历背包
                if(j-wight[i]>=0)
                    dp[i][j]=Math.max(dp[i-1][j],(dp[i-1][j-wight[i]]+value[i]));
            }
        }
        //打印dp数组
        System.out.println("=====递推后的·dp=====");
        printDP(dp);

        return dp[wight.length-1][bagW];
    }

    //打印dp数组
    public static void printDP(int [][]dp){
        for (int i = 0; i < dp.length; i++) {
            for (int j = 0; j < dp[0].length; j++) {
                System.out.print(dp[i][j]+" ");
            }
            System.out.println();
        }
    }

}

在这里插入图片描述

2.01背包（滚动数组实现）

在使⽤⼆维数组的时候，递推公式：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] +value[i]);
其实可以发现如果把dp[i - 1]那⼀层拷贝到dp[i]上，表达式完全可以是：dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]); 于其把dp[i -1]这⼀层拷贝到dp[i]上，不如只⽤⼀个⼀维数组了，只⽤dp[j]（⼀维数组，也可以理解是⼀个滚动数组）。

1. 确定dp数组的定义

在⼀维dp数组中，dp[j]表⽰：容量为j的背包，所背的物品价值可以最⼤为dp[j]。

2.递推公式

dp[j] = max(dp[j], dp[j - weight[i]] + value[i])

java代码

//01背包（一维滚动数组实现）
    //在⼀维dp数组中，dp[j]表⽰：容量为j的背包，所背的物品价值可以最⼤为dp[j]。
    public static int knapsack02(){
        int weight[]={1,3,4};
        int value[]={15,20,30};
        int bagW=4;
        int []dp=new int[bagW+1];//默认初始化为0

        for(int i = 0; i < weight.length; i++) { // 遍历物品
            for(int j = bagW; j >= weight[i]; j--) { // 遍历背包容量
                dp[j] = Math.max(dp[j], dp[j-weight[i]]+value[i]);
            }
        }
        return dp[bagW];
    }

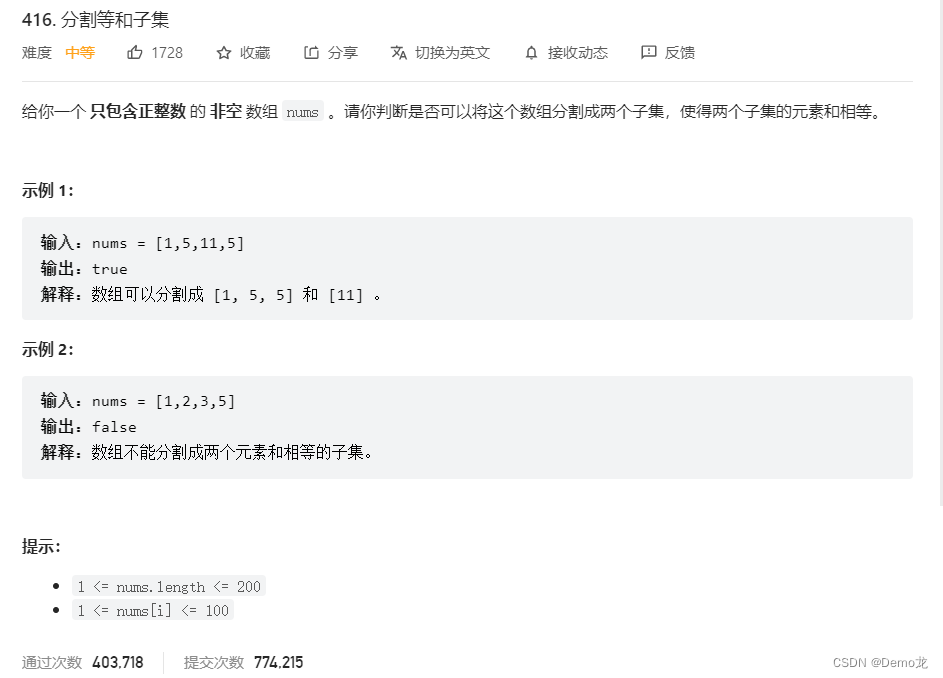
在这里插入图片描述

1.416. 分割等和子集

链接: 416. 分割等和子集
在这里插入图片描述

class Solution {
    public boolean canPartition(int[] nums) {
        int target=0;
        for(int i=0;i<nums.length;i++){
            target+=nums[i];
        }
        if(target%2!=0){
            return false;
        }
        target=target/2;
        int dp[]=new int[target+1];//默认初始化为0
        for(int i=0;i<nums.length;i++){//先遍历物品
            for(int j=target;j>=nums[i];j--){//倒序遍历背包，确保每个物品只能进入一次
                dp[j]=Math.max(dp[j],dp[j-nums[i]]+nums[i]);
            }
        }
        if(dp[target]==target){
            return true;
        }
        return false;

    }
}

2.1049. 最后一块石头的重量 II

链接: 1049. 最后一块石头的重量 II
在这里插入图片描述

class Solution {
    public int lastStoneWeightII(int[] stones) {
        int sum=0;
        for(int i=0;i<stones.length;i++){
            sum+=stones[i];
        }
        int target=sum/2;//将stones数组一分为二，找到重量最接近target的dp数组
        int dp[]=new int[target+1];//默认初始化为0
        for(int i=0;i<stones.length;i++){//先遍历石头
            for(int j=target;j>=stones[i];j--){//再逆序遍历背包
                dp[j]=Math.max(dp[j],dp[j-stones[i]]+stones[i]);
            }
        }
        int min_Weight=(sum-dp[target])-dp[target];//一分为二的石头相减得到最小重量
        return min_Weight;
    }
}

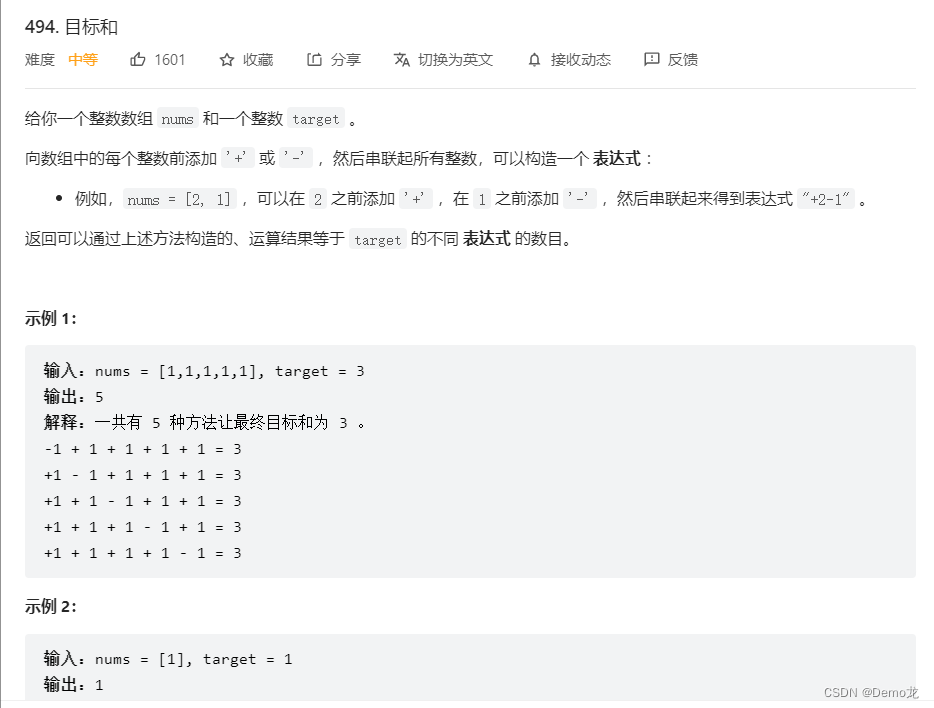
*3.494. 目标和

链接: 494. 目标和
在这里插入图片描述

在这里插入图片描述

class Solution {
    public int findTargetSumWays(int[] nums, int target) {
        int sum = 0;
        for (int i = 0; i < nums.length; i++) 
            sum += nums[i];

        if(Math.abs(target)>sum){//如果target的绝对值大于sum，此时没有方案
            return 0;
        }

        if ((target + sum) % 2 == 1) 
            return 0; // 此时没有⽅案

        int bagSize=(sum+target)/2;
        int dp[]=new int[bagSize+1];
        dp[0]=1;
        for(int i=0;i<nums.length;i++){
            for(int j=bagSize;j>=nums[i];j--){
                dp[j]+=dp[j-nums[i]];
            }
        }
        return dp[bagSize];
    }
}

4.474. 一和零

链接: 474. 一和零
在这里插入图片描述

class Solution {
    public int findMaxForm(String[] strs, int m, int n) {
        int dp[][]=new int[m+1][n+1];//默认初始化为0；

        for(String str:strs){
            int num1=0;int num0=0;
            for(char c:str.toCharArray()){
                if(c=='1'){
                    num1++;
                }else{
                    num0++;
                }
            }
            for(int i=m;i>=num0;i--){
                for(int j=n;j>=num1;j--){
                    dp[i][j]=Math.max(dp[i][j],dp[i-num0][j-num1]+1);
                }
            }
        }
        return dp[m][n];

    }
}

2.完全背包

public class CompleteBackpack {
    //完全背包问题
    public static void main(String[] args) {
        System.out.println(test_CompletePack());
    }
    // 先遍历物品，在遍历背包
    public static int test_CompletePack() {
        int []weight = {1, 3, 4};
        int []value = {15, 20, 30};
        int bagWeight = 4;
        int dp[]=new int[bagWeight + 1];
        for(int i = 0; i < weight.length; i++) { // 遍历物品
            for(int j = weight[i]; j <= bagWeight; j++) { // 遍历背包容量
                //正序遍历，每个物品可以选多次
                dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
            }
        }
        return dp[bagWeight];
    }
}

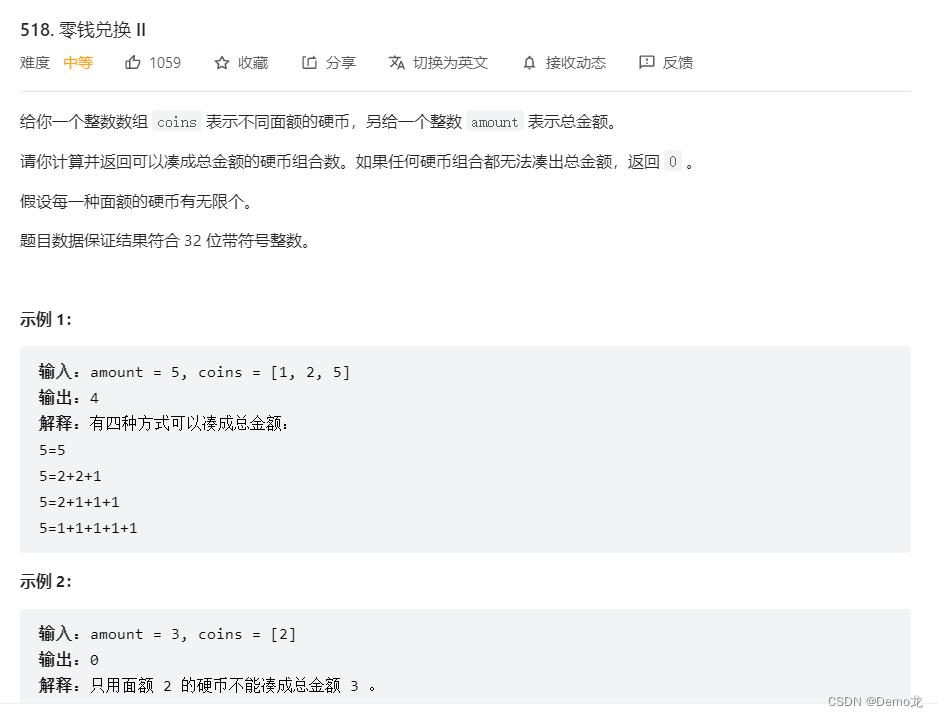
1.518. 零钱兑换 II

链接: 518. 零钱兑换 II
在这里插入图片描述

class Solution {
    public int change(int amount, int[] coins) {
        int n=coins.length;
        int dp[]=new int[amount+1];//默认初始化为0
        dp[0]=1;//初始化不放入物品的方式有一种
        for(int i=0;i<n;i++){
            for(int j=coins[i];j<=amount;j++){
                dp[j]+=dp[j-coins[i]];
            }
        }
        return dp[amount];
    }
}

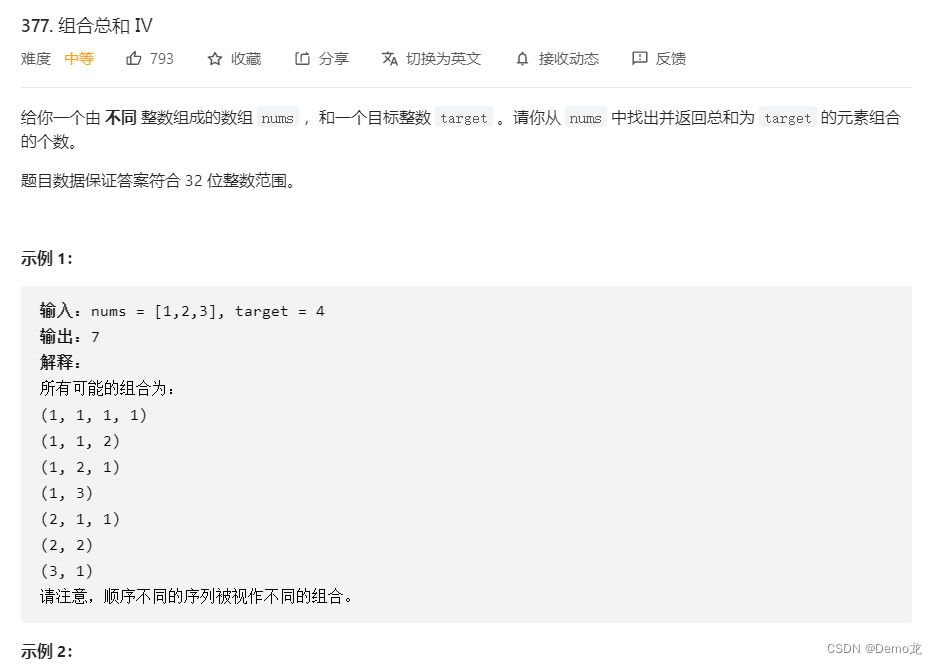
2.377. 组合总和 Ⅳ

链接: 377. 组合总和 Ⅳ
在这里插入图片描述

class Solution {
    public int combinationSum4(int[] nums, int target) {
        int dp[]=new int[target+1];
        dp[0]=1;
        for(int i=0;i<=target;i++){
            for(int j=0;j<nums.length;j++){
                if (i >= nums[j] )
                    dp[i]+=dp[i-nums[j]];
            }
        }
        return dp[target];
    }
}

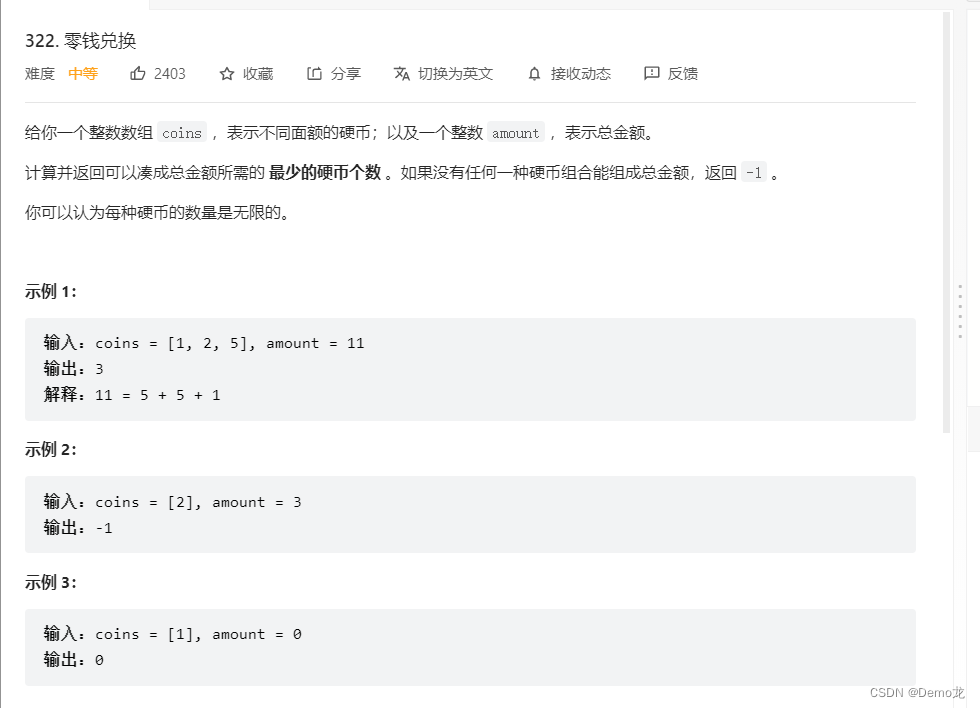
3.322. 零钱兑换

链接: 322. 零钱兑换
在这里插入图片描述

class Solution {
    public int coinChange(int[] coins, int amount) {
        int n=coins.length;
        int dp[]=new int[amount+1];//默认初始化为0
        dp[0]=0;//先凑⾜总⾦额为0所需钱币的个数⼀定是0
        for(int i=1;i<=amount;i++){
            dp[i]=Integer.MAX_VALUE;
        }
        for(int i=0;i<n;i++){
            for(int j=coins[i];j<=amount;j++){
                if(dp[j-coins[i]]!=Integer.MAX_VALUE)
                dp[j]=Math.min(dp[j-coins[i]]+1,dp[j]);
            }
        }
        if(dp[amount]==Integer.MAX_VALUE)
            return -1;
        return dp[amount];
    }
}

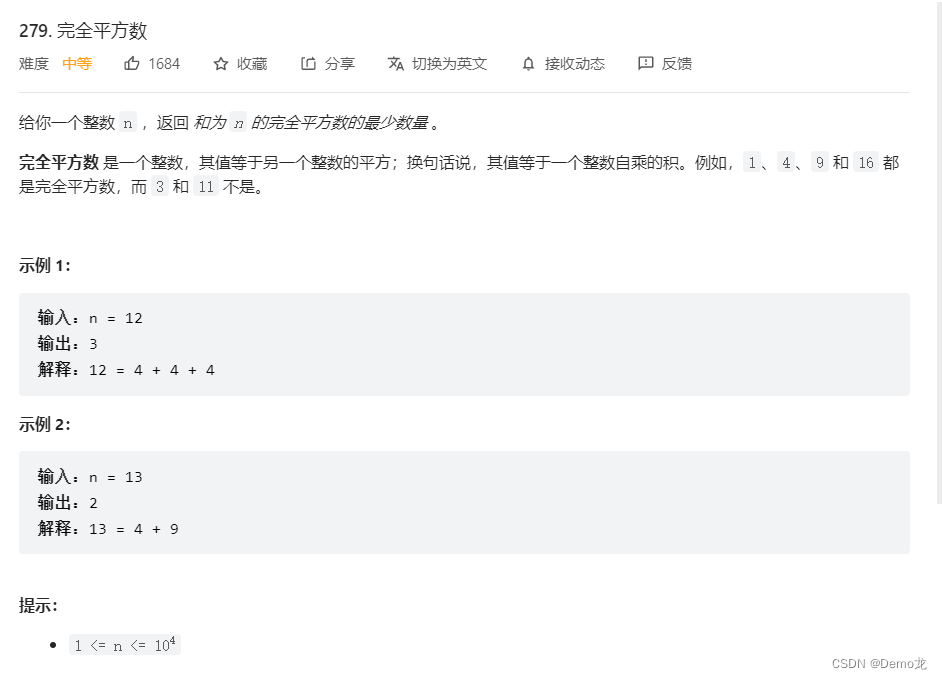
4.279. 完全平方数

链接: 279. 完全平方数
在这里插入图片描述

class Solution {
    public int numSquares(int n) {
        int dp[]=new int[n+1];
        dp[0]=0;
        for(int i=1;i<=n;i++){
            dp[i]=Integer.MAX_VALUE;
        }
        for(int i=0;i*i<=n;i++){
            for(int j=i*i;j<=n;j++){
                if(dp[j-i*i]!=Integer.MAX_VALUE)
                    dp[j]=Math.min(dp[j-i*i]+1,dp[j]);
            }
        }
        return dp[n];
    }
}

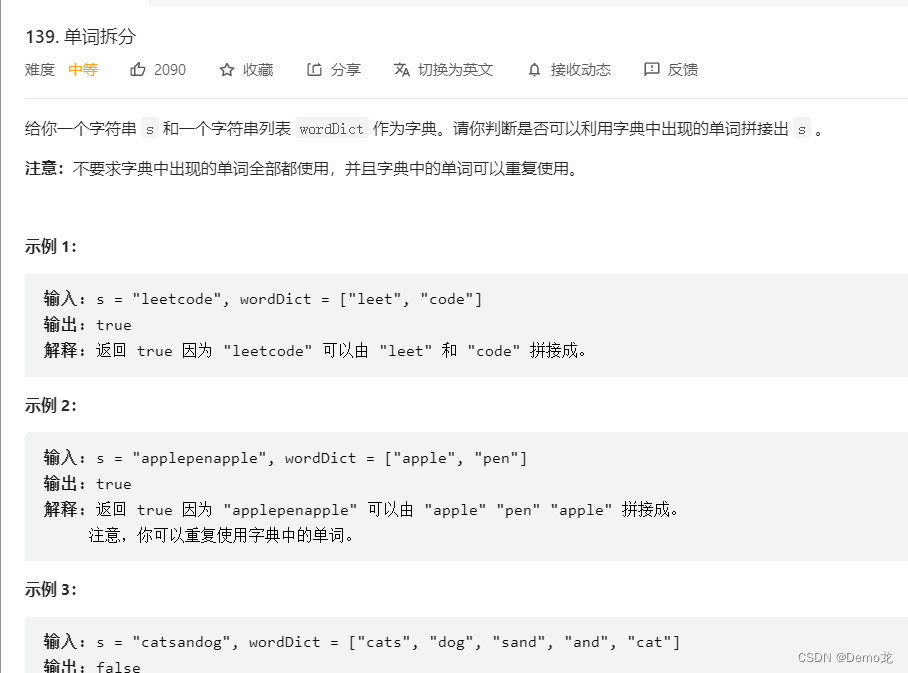
*5.139. 单词拆分

链接: 139. 单词拆分
在这里插入图片描述

class Solution {
    public boolean wordBreak(String s, List<String> wordDict) {
        int n=s.length();
        boolean[] dp = new boolean[n + 1];
        dp[0]=true;
        for(int i=0;i<=n;i++){
            for(int j=0;j<i;j++){
                if(dp[j]&&wordDict.contains(s.substring(j,i))){
                    dp[i]=true;
                    break;
                }
            }
        }
        return dp[n];
    }
}

3.打家劫舍

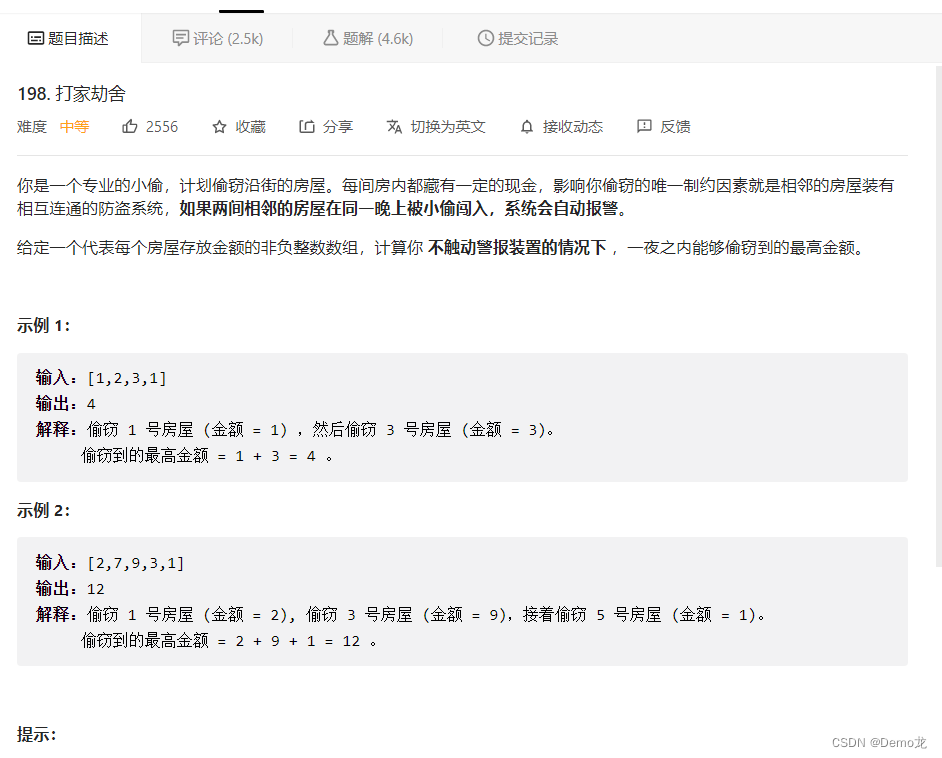
1.198. 打家劫舍

链接: 198. 打家劫舍
在这里插入图片描述

class Solution {
    public int rob(int[] nums) {
        int n=nums.length;
        if(n<=1){
            return nums[0];
        }
        int dp[]=new int[n];//默认初始化为0
        dp[0]=nums[0];
        dp[1]=Math.max(nums[0],nums[1]);
        for(int i=2;i<n;i++){
            dp[i]=Math.max((nums[i]+dp[i-2]),dp[i-1]);
        }
        return dp[n-1];
    }
}

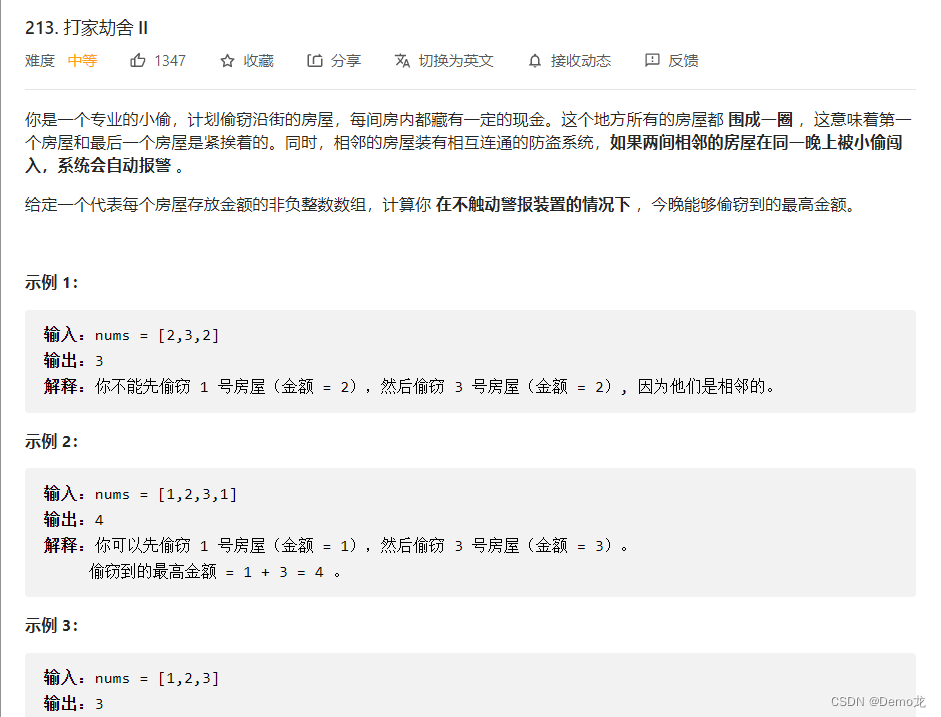
2.213. 打家劫舍 II

链接: 213. 打家劫舍 II
在这里插入图片描述

class Solution {
    public int rob(int[] nums) {
        int n=nums.length;
        if(n<=1){
            return nums[0];
        }else if(n==2){
            return Math.max(nums[0],nums[1]);
        }
        return Math.max(fun(nums,0,n-1),fun(nums,1,n));
    }
     public int fun(int[] nums,int i,int n) {
        int dp[]=new int[n];//默认初始化为0
        dp[i]=nums[i];
        dp[i+1]=Math.max(nums[i],nums[i+1]);
        for(int j=i+2;j<n;j++){
            dp[j]=Math.max((nums[j]+dp[j-2]),dp[j-1]);
        }
        return dp[n-1];
    }
}

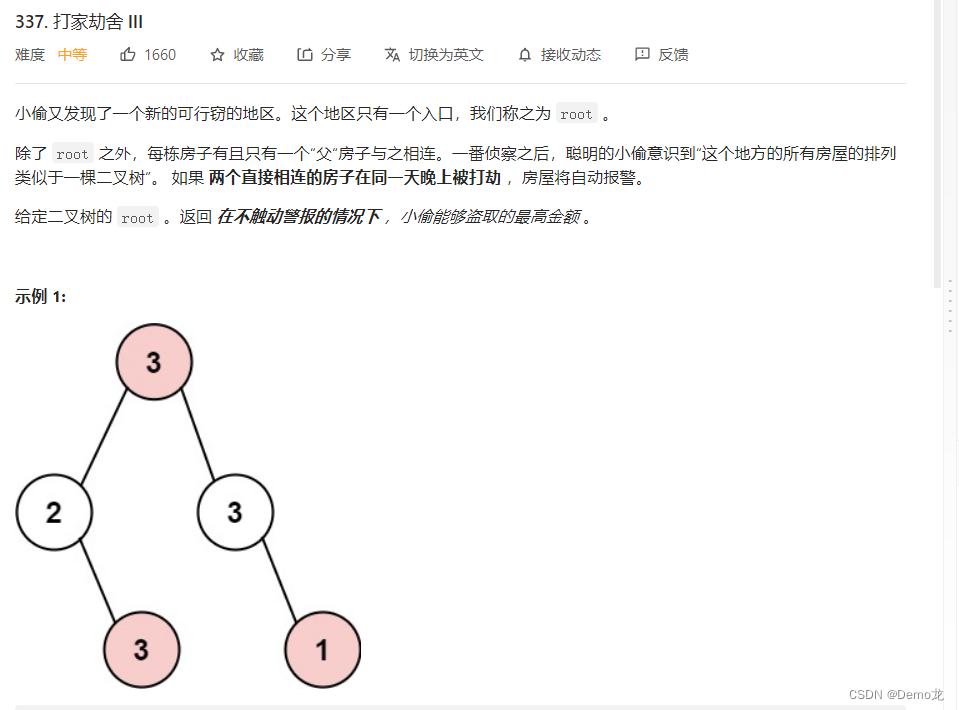
3.337. 打家劫舍 III

链接: 337. 打家劫舍 III
在这里插入图片描述

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int rob(TreeNode root) {
        int result[] = robTree(root);
        return Math.max(result[0], result[1]);
    }
    // ⻓度为2的数组，0：不偷，1：偷
    int[] robTree(TreeNode cur) {
        if (cur == null) 
            return new int[]{0, 0};
        int left[] = robTree(cur.left);
        int right[] = robTree(cur.right);
        // 偷cur
        int val1 = cur.val + left[0] + right[0];
        // 不偷cur
        int val2 = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
        return new int[]{val2, val1};
    }
}

4.股票问题

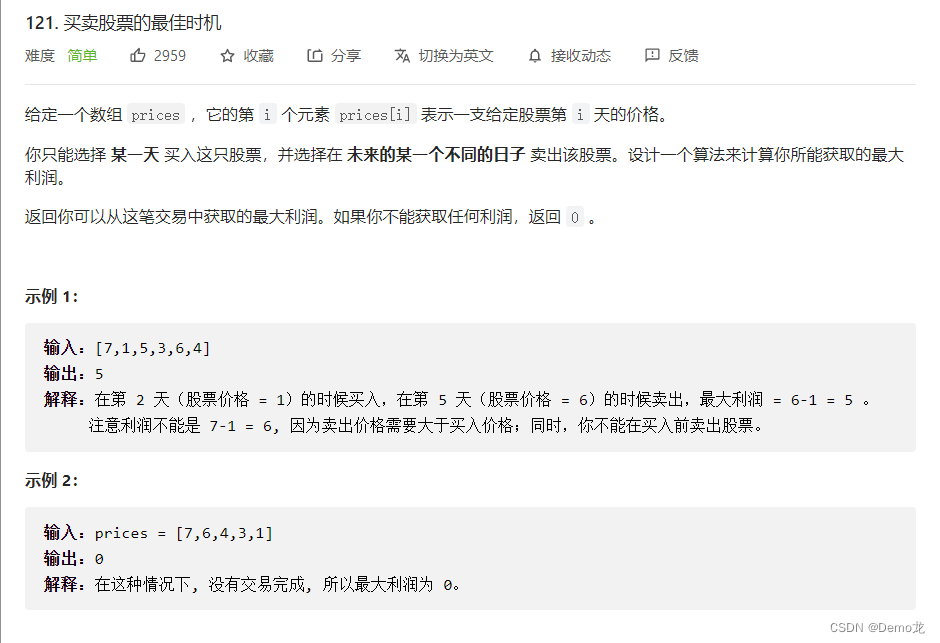
1.121. 买卖股票的最佳时机

链接: 121. 买卖股票的最佳时机
在这里插入图片描述

class Solution {
    public int maxProfit(int[] prices) {
        int n=prices.length;
        if(n==0){
            return 0;
        }
        int [][]dp=new int[n][2];
        dp[0][0]=-prices[0];
        dp[0][1]=0;
        for(int i=1;i<n;i++){
            dp[i][0]=Math.max(dp[i-1][0],-prices[i]);
            dp[i][1]=Math.max(dp[i-1][1],prices[i]+dp[i-1][0]);
        }
        return dp[n-1][1];
    }
}

2.122. 买卖股票的最佳时机 II

链接: 122. 买卖股票的最佳时机 II

class Solution {
    public int maxProfit(int[] prices) {
        int n=prices.length;
        if(n==0){
            return 0;
        }
        int [][]dp=new int[n][2];
        dp[0][0]=-prices[0];
        dp[0][1]=0;
        for(int i=1;i<n;i++){
            dp[i][0]=Math.max(dp[i-1][0],dp[i-1][1]-prices[i]);//和1唯一不同
            dp[i][1]=Math.max(dp[i-1][1],prices[i]+dp[i-1][0]);
        }
        return dp[n-1][1];
    }
}

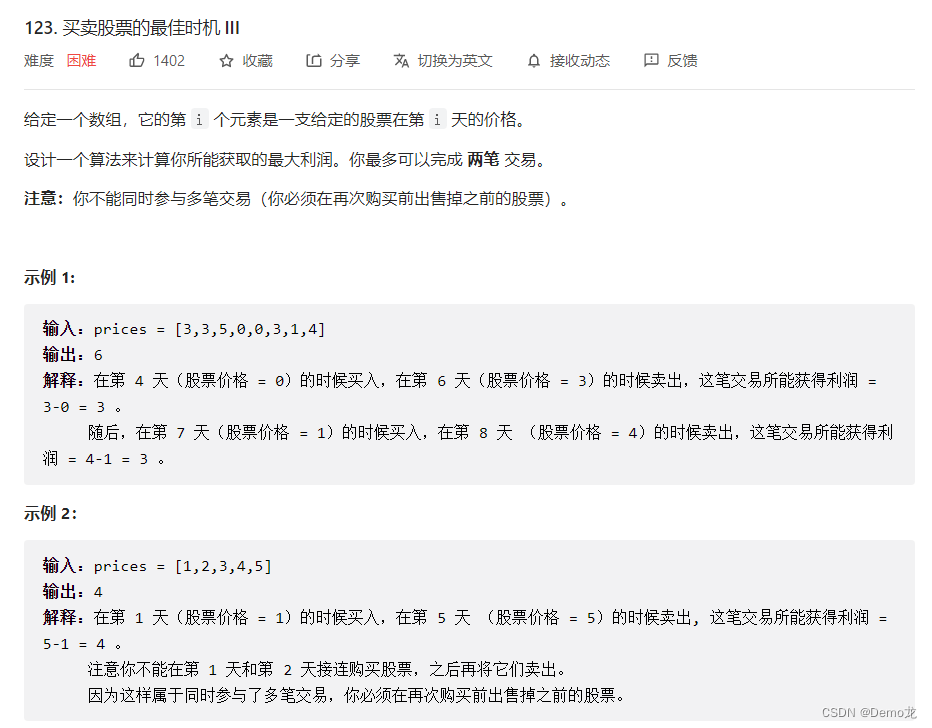
3.123. 买卖股票的最佳时机 III

链接: 123. 买卖股票的最佳时机 III
在这里插入图片描述


class Solution {
    public int maxProfit(int[] prices) {
        int n=prices.length;
        if(n==0){
            return 0;
        }
        int [][]dp=new int[n][4];
        dp[0][0]=-prices[0];//第一次持有
        dp[0][1]=0;//第一次不持有
        dp[0][2]=-prices[0];//第二次持有
        dp[0][3]=0;//第二次不持有
        for(int i=1;i<n;i++){
            dp[i][0]=Math.max(dp[i-1][0],-prices[i]);
            dp[i][1]=Math.max(dp[i-1][1],dp[i-1][0]+prices[i]);
            dp[i][2]=Math.max(dp[i-1][2],dp[i-1][1]-prices[i]);
            dp[i][3]=Math.max(dp[i-1][3],dp[i-1][2]+prices[i]);
        }
        return dp[n-1][3];
    }
}

4.188. 买卖股票的最佳时机 IV

链接: 188. 买卖股票的最佳时机 IV
在这里插入图片描述

class Solution {
    public int maxProfit(int k, int[] prices) {
        int n=prices.length;
        if(n==0)
            return 0;
        int [][]dp=new int[n][2*k+1];//初始化默认为0
        for(int j=1;j<2*k;j+=2){
            dp[0][j]=-prices[0];//第j次持有
        }
        for(int i=1;i<n;i++){
            for(int j=0;j<2*k;j+=2){
                dp[i][j+1]=Math.max(dp[i-1][j+1],dp[i-1][j]-prices[i]);
                dp[i][j+2]=Math.max(dp[i-1][j+2],dp[i-1][j+1]+prices[i]);
            }
        }
        return dp[n-1][2*k];
    }
}

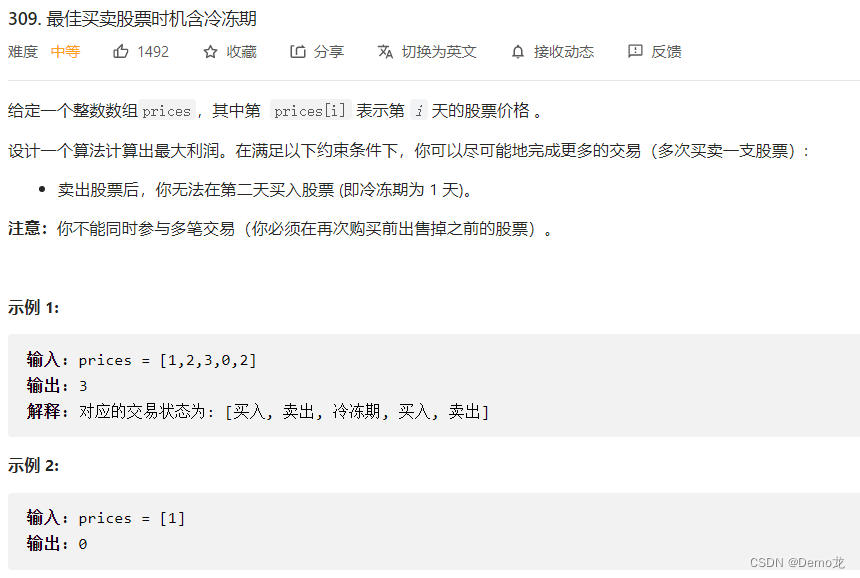
5.309. 最佳买卖股票时机含冷冻期

链接: 309. 最佳买卖股票时机含冷冻期
在这里插入图片描述

class Solution {
    public int maxProfit(int[] prices) {
        int n=prices.length;
        if(n==0){
            return 0;
        }
        int [][]dp=new int[n][4];
        dp[0][0]=-prices[0];//持股
        dp[0][1]=0;//保持卖出股
        dp[0][2]=0;//卖出股
        dp[0][3]=0;//冷冻期
        for(int i=1;i<n;i++){
            dp[i][0]=Math.max(dp[i-1][0],Math.max(dp[i-1][1],dp[i-1][3])-prices[i]);
            dp[i][1]=Math.max(dp[i-1][1],dp[i-1][3]);
            dp[i][2]=dp[i-1][0]+prices[i];
            dp[i][3]=dp[i-1][2];
        }
        return Math.max(dp[n - 1][3],Math.max(dp[n - 1][1], dp[n - 1][2]));
    }
}

6.714. 买卖股票的最佳时机含手续费

链接: 714. 买卖股票的最佳时机含手续费
在这里插入图片描述

class Solution {
    public int maxProfit(int[] prices, int fee) {
        int n=prices.length;
        if(n==0){
            return 0;
        }
        int [][]dp=new int[n][2];
        dp[0][0]=-prices[0];
        dp[0][1]=0;
        for(int i=1;i<n;i++){
            dp[i][0]=Math.max(dp[i-1][0],dp[i-1][1]-prices[i]);
            dp[i][1]=Math.max(dp[i-1][1],prices[i]+dp[i-1][0]-fee);
        }
        return dp[n-1][1];
    }
}

5.子序列问题

1.子序列（不连续）

1.300. 最长递增子序列

链接: 300. 最长递增子序列
在这里插入图片描述

class Solution {
    public int lengthOfLIS(int[] nums) {
        int n=nums.length;
        if(n<=1){
            return n;
        }
        int dp[]=new int[n];
        for(int i=0;i<n;i++){
            dp[i]=1;
        }
        int result=0;
        for(int i=1;i<n;i++){
            for(int j=0;j<i;j++){
                if(nums[i]>nums[j]){
                    dp[i]=Math.max(dp[j]+1,dp[i]);
                }
            }
            result=Math.max(result,dp[i]);
        }
        return result;
    }
}

2.1143. 最长公共子序列

链接: 1143. 最长公共子序列
在这里插入图片描述


class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        char []nums1=text1.toCharArray();
        char []nums2=text2.toCharArray();
        int n1=nums1.length;
        int n2=nums2.length;
        int dp[][]=new int[n1+1][n2+1];//默认初始化为0
        int result=0;
        for(int i=1;i<=n1;i++){
            for(int j=1;j<=n2;j++){
                if(nums1[i-1]==nums2[j-1]){
                    dp[i][j]=dp[i-1][j-1]+1;
                }else{
                    dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);
                }
            }
        }
        return dp[n1][n2];
    }
}

3.1035. 不相交的线

链接: 1035. 不相交的线
在这里插入图片描述


class Solution {//和上一题一摸一样，求最长公共子序列
    public int maxUncrossedLines(int[] nums1, int[] nums2) {
        int n1=nums1.length;
        int n2=nums2.length;
        int dp[][]=new int[n1+1][n2+1];//默认初始化为0
        int result=0;
        for(int i=1;i<=n1;i++){
            for(int j=1;j<=n2;j++){
                if(nums1[i-1]==nums2[j-1]){
                    dp[i][j]=dp[i-1][j-1]+1;
                }else{
                    dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);
                }
            }
        }
        return dp[n1][n2];
    }
}

2.子序列（连续）

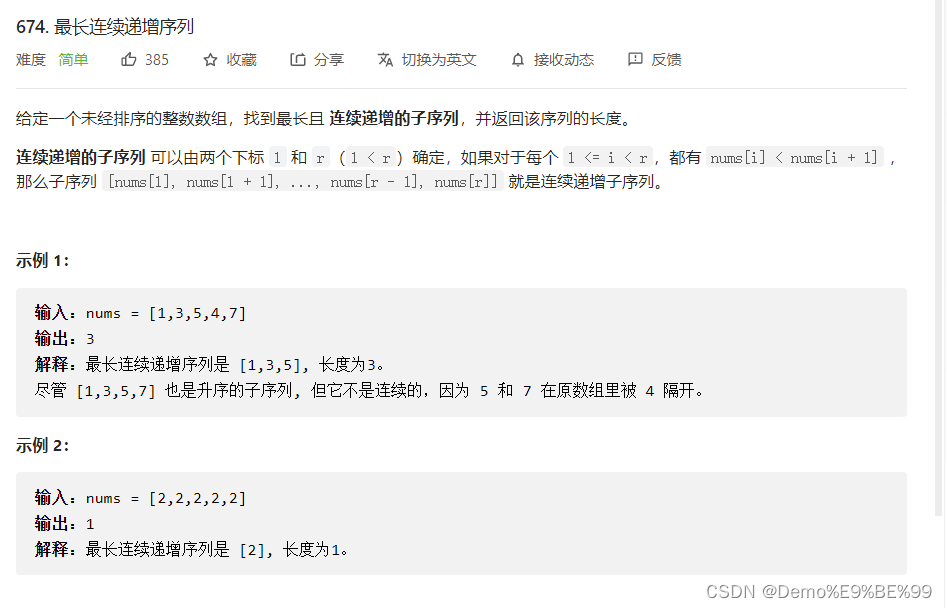
1.674. 最长连续递增序列

链接: 674. 最长连续递增序列
在这里插入图片描述

class Solution {
    public int findLengthOfLCIS(int[] nums) {
        int n=nums.length;
        if(n<=1){
            return n;
        }
        int dp[]=new int[n];
        for(int i=0;i<n;i++){
            dp[i]=1;
        }
        int result=0;
        for(int i=1;i<n;i++){
                if(nums[i]>nums[i-1]){
                    dp[i]=dp[i-1]+1;
                }
            result=Math.max(result,dp[i]);
        }
        return result;
    }
}

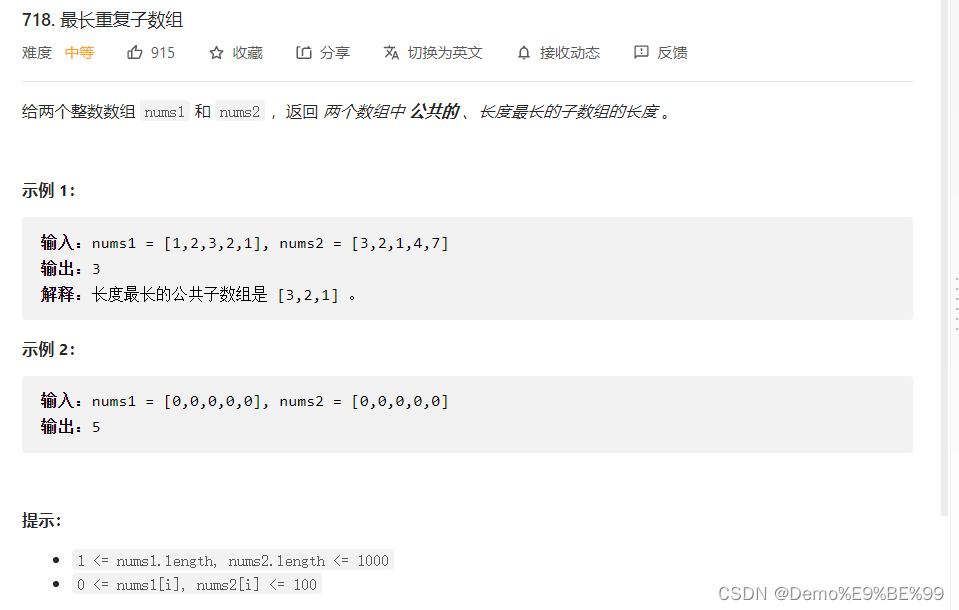
*2.718. 最长重复子数组

链接: 718. 最长重复子数组
在这里插入图片描述

class Solution {
    public int findLength(int[] nums1, int[] nums2) {
        int n1=nums1.length;
        int n2=nums2.length;
        int dp[][]=new int[n1+1][n2+1];//默认初始化为0
        int result=0;
        for(int i=1;i<=n1;i++){
            for(int j=1;j<=n2;j++){
                if(nums1[i-1]==nums2[j-1]){
                    dp[i][j]=dp[i-1][j-1]+1;
                }
                result=Math.max(result,dp[i][j]);

            }
        }
        return result;
    }
}

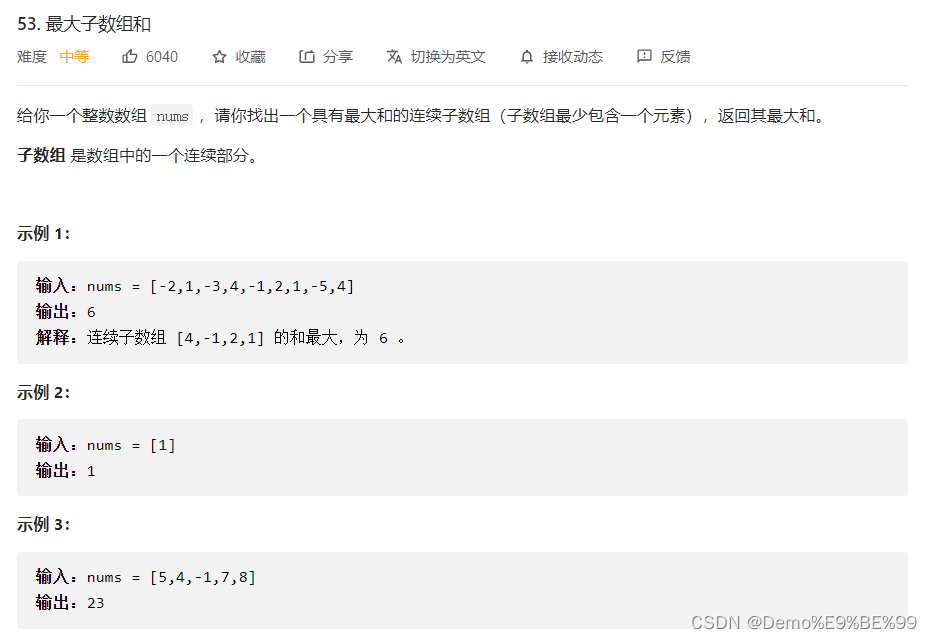
3.53. 最大子数组和

链接: 53. 最大子数组和
在这里插入图片描述

class Solution {
    public int maxSubArray(int[] nums) {
        int n=nums.length;
        int dp[]=new int [n];
        dp[0]=nums[0];
        int result=dp[0];
        for(int i=1;i<n;i++){
            dp[i]=Math.max(dp[i-1]+nums[i],nums[i]);
            result=Math.max(dp[i],result);
        }
        return result;
    }
}

3.编辑距离

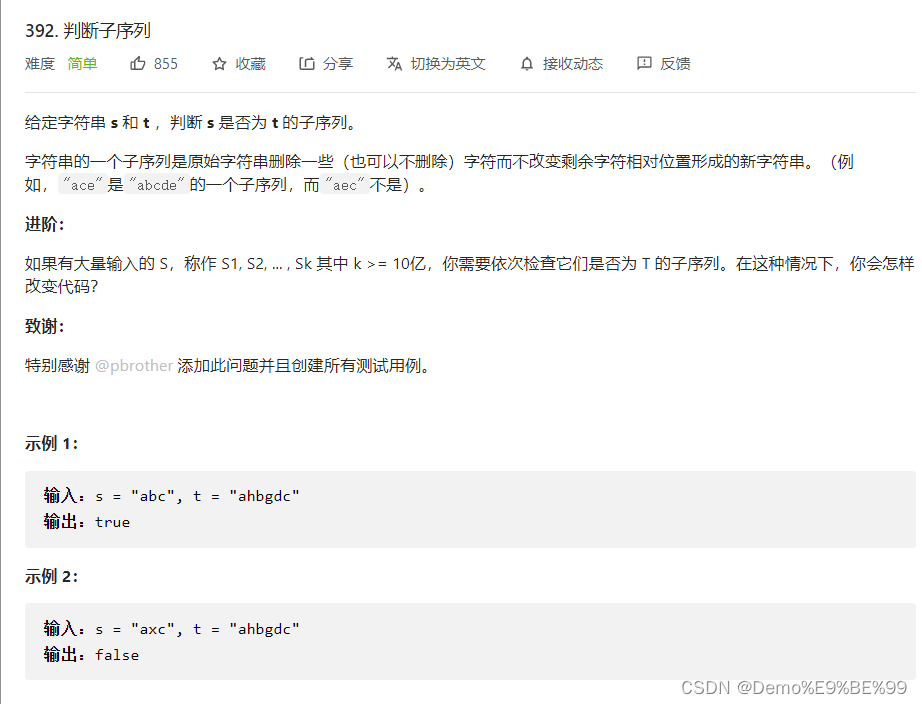
1.392. 判断子序列

链接: 392. 判断子序列
在这里插入图片描述

class Solution {
    public boolean isSubsequence(String s, String t) {
        char []nums1=s.toCharArray();
        char []nums2=t.toCharArray();
        int n1=nums1.length;
        int n2=nums2.length;
        int dp[][]=new int[n1+1][n2+1];//默认初始化为0
        for(int i=1;i<=n1;i++){
            for(int j=1;j<=n2;j++){
                if(nums1[i-1]==nums2[j-1]){
                    dp[i][j]=dp[i-1][j-1]+1;
                }else{
                    dp[i][j]=dp[i][j-1];
                }
            }
        }
        if(dp[n1][n2]==n1){
            return true;
        }
        return false;
    }
}

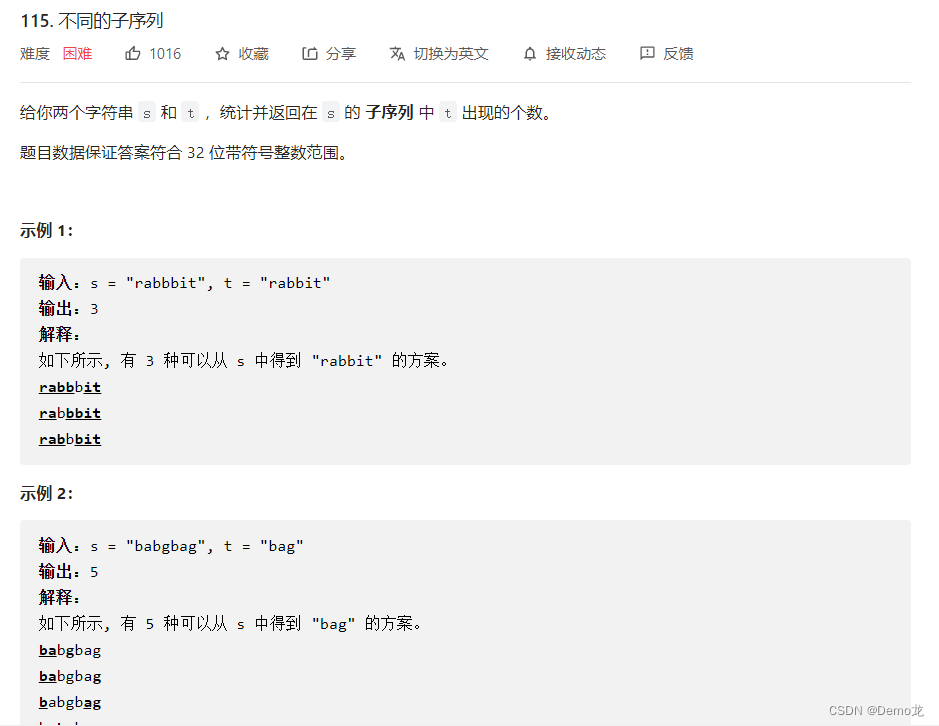
2.115. 不同的子序列

链接: 115. 不同的子序列
在这里插入图片描述

class Solution {
    public int numDistinct(String s, String t) {
        int n1=s.length();
        int n2=t.length();
        int [][]dp=new int[n1+1][n2+1];//默认为0
        for(int i=0;i<n1;i++){
            dp[i][0]=1;
        }

        for(int i=1;i<=n1;i++){
            for(int j=1;j<=n2;j++){
                if (j > i)
                    continue;
                if(s.charAt(i-1)==t.charAt(j-1)){
                    dp[i][j]=dp[i-1][j-1]+dp[i-1][j];
                }else{
                    dp[i][j]=dp[i-1][j];
                }
            }
        }
        return dp[n1][n2];
    }
}

3.583. 两个字符串的删除操作

链接: 583. 两个字符串的删除操作
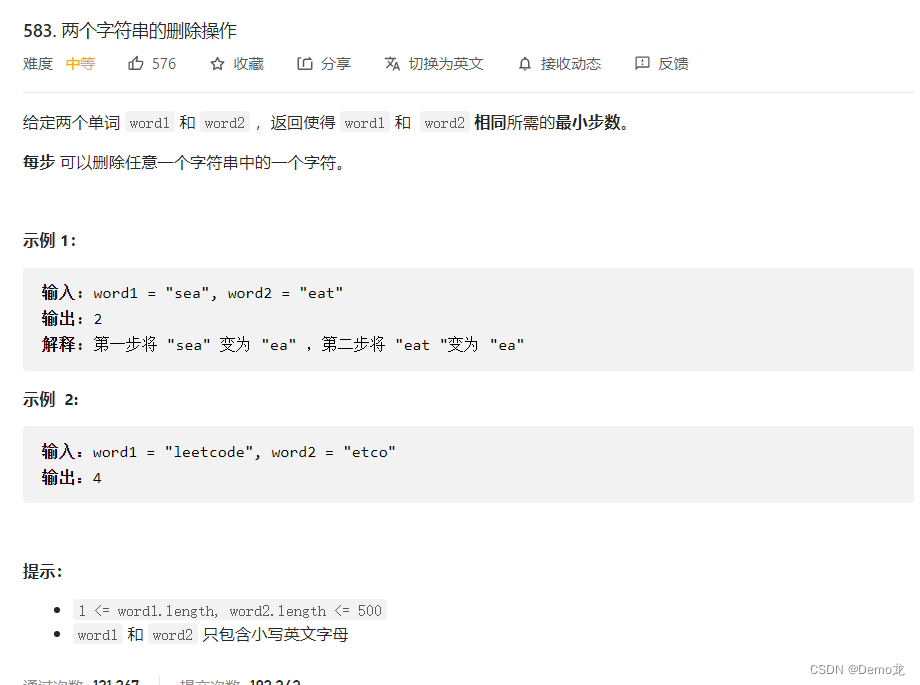
在这里插入图片描述
方法一，动态规划思路解决

class Solution {
    public int minDistance(String word1, String word2) {
        int n1=word1.length();
        int n2=word2.length();
        int [][]dp=new int[n1+1][n2+1];//默认为0
        for(int i=0;i<=n1;i++){
            dp[i][0]=i;
        }
        for(int j=0;j<=n2;j++){
            dp[0][j]=j;
        }

        for(int i=1;i<=n1;i++){
            for(int j=1;j<=n2;j++){
                if(word1.charAt(i-1)==word2.charAt(j-1)){
                    dp[i][j]=dp[i-1][j-1];
                }else{
                    dp[i][j]=
                    Math.min(dp[i-1][j-1]+2,
                    Math.min(dp[i-1][j]+1,dp[i][j-1]+1));
                }
            }
        }
        return dp[n1][n2];
    }
}

方法二，求公共最大子序列，len1+len2-最大子序列长度即为需要删除的数目

//方法二
class Solution {
    public int minDistance(String word1, String word2) {
        int n1=word1.length();
        int n2=word2.length();
        int dp[][]=new int[n1+1][n2+1];//默认初始化为0
        int result=0;
        for(int i=1;i<=n1;i++){
            for(int j=1;j<=n2;j++){
                if(word1.charAt(i-1)==word2.charAt(j-1)){
                    dp[i][j]=dp[i-1][j-1]+1;
                }else{
                    dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);
                }
            }
        }
        return n1+n2-2*dp[n1][n2];
    }
}

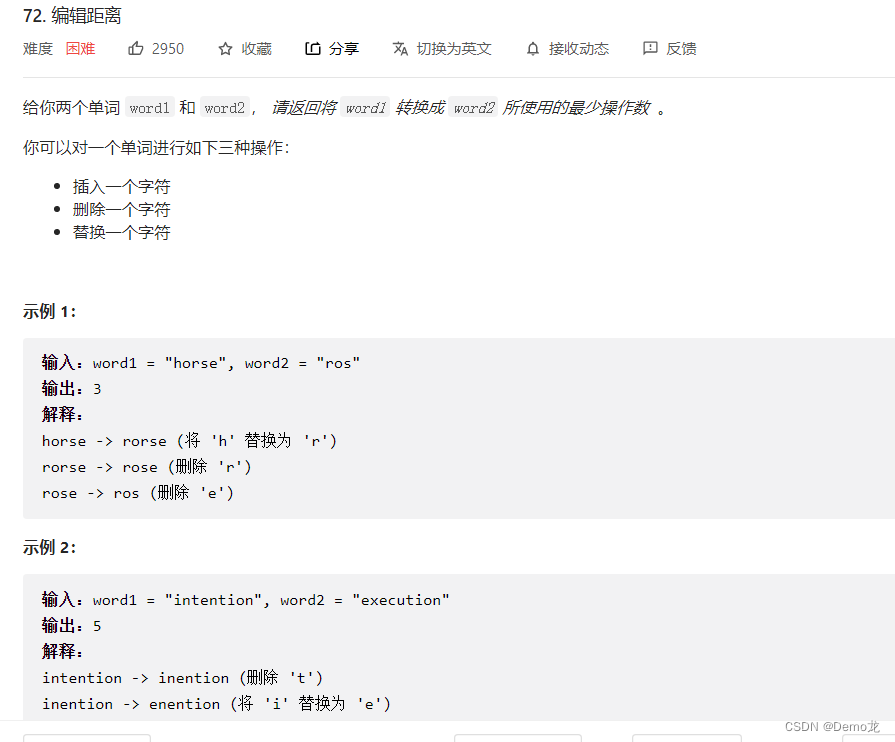
4.72. 编辑距离

链接: 72. 编辑距离
在这里插入图片描述

class Solution {
    public int minDistance(String word1, String word2) {
        int n1=word1.length();
        int n2=word2.length();
        int [][]dp=new int[n1+1][n2+1];//默认为0
        for(int i=0;i<=n1;i++){
            dp[i][0]=i;
        }
        for(int j=0;j<=n2;j++){
            dp[0][j]=j;
        }
        for(int i=1;i<=n1;i++){
            for(int j=1;j<=n2;j++){
                if(word1.charAt(i-1)==word2.charAt(j-1)){
                    dp[i][j]=dp[i-1][j-1];
                }else{
                    dp[i][j]=
                    Math.min(dp[i-1][j-1]+1,
                                Math.min(dp[i-1][j]+1,dp[i][j-1]+1));
                }
            }
        }
        return dp[n1][n2];
    }
}

4.回文

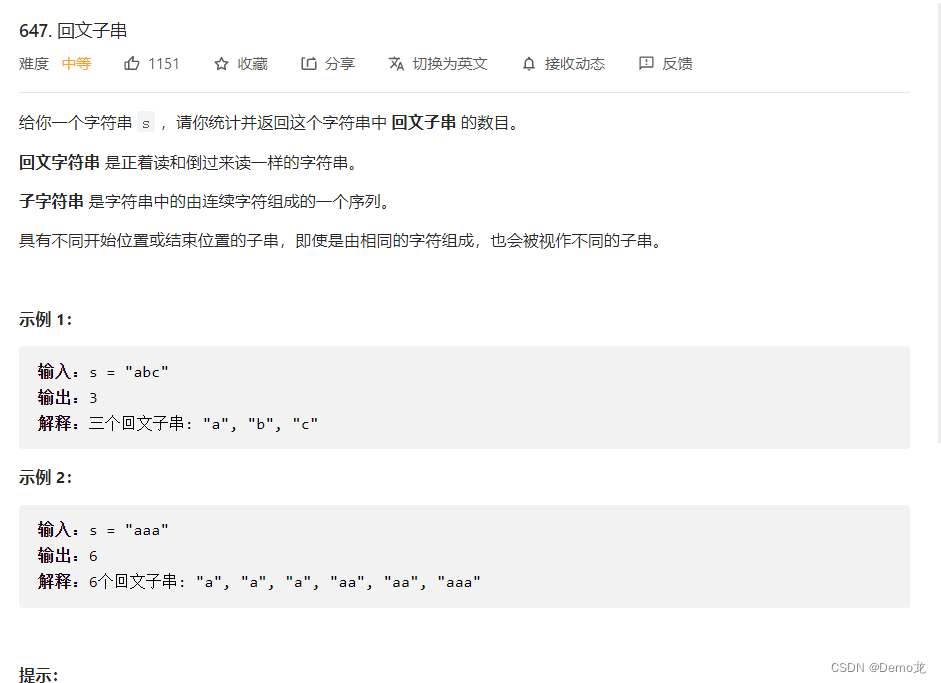
1.647. 回文子串

链接: 647. 回文子串
在这里插入图片描述

class Solution {
    public int countSubstrings(String s) {
        int n=s.length();
        int dp[][]=new int[n+1][n+1];
        int result=0;
        for(int i=n-1;i>=0;i--){
            for(int j=i;j<n;j++){
                if(s.charAt(i)==s.charAt(j)){
                    if(j-i<=1){
                        dp[i][j]=1;
                        result++;
                    }else if(dp[i+1][j-1]==1){
                    dp[i][j]=1;
                    result++;
                    }
                }
            }
        }
        return result;
    }
}

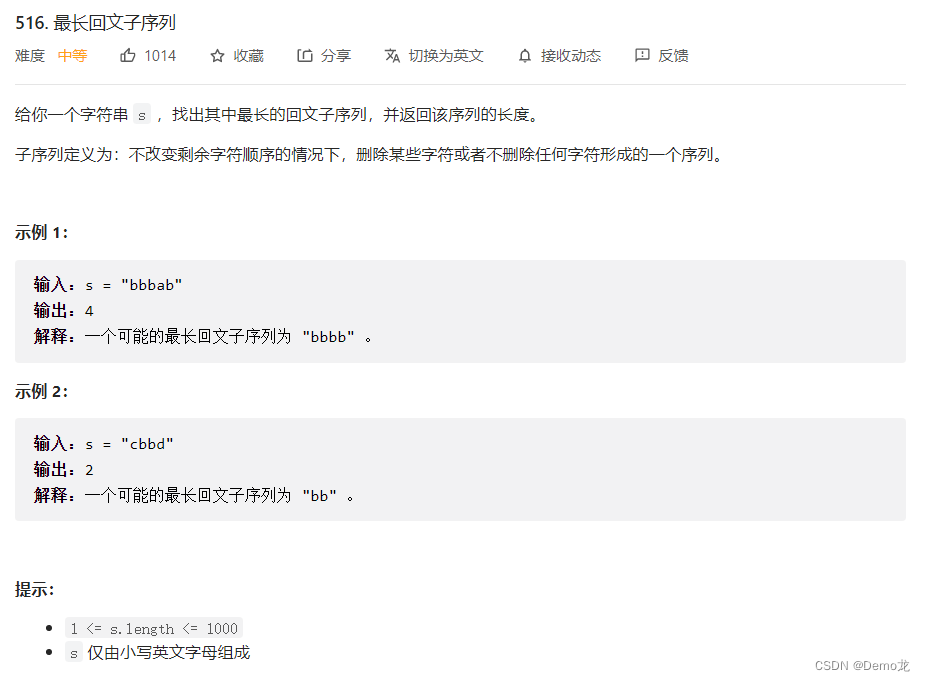
2.516. 最长回文子序列

链接: 516. 最长回文子序列
在这里插入图片描述

class Solution {
    public int longestPalindromeSubseq(String s) {
        int n=s.length();
        int dp[][]=new int[n+1][n+1];
        for(int i=0;i<n;i++){
            dp[i][i]=1;
        }
        for(int i=n-1;i>=0;i--){
            for(int j=i+1;j<n;j++){
                if(s.charAt(i)==s.charAt(j)){
                    dp[i][j]=dp[i+1][j-1]+2;
                }else {
                    dp[i][j]=Math.max(dp[i+1][j],dp[i][j-1]);
                }
            }
        }
        return dp[0][n-1];
    }
}