从零实现深度学习框架——常见学习率调整策略原理与实现

news2025/1/12 1:46:23

引言

本着“凡我不能创造的，我就不能理解”的思想，本系列文章会基于纯Python以及NumPy从零创建自己的深度学习框架，该框架类似PyTorch能实现自动求导。
💡系列文章完整目录： 👉点此👈
要深入理解深度学习，从零开始创建的经验非常重要，从自己可以理解的角度出发，尽量不适用外部框架的前提下，实现我们想要的模型。本系列文章的宗旨就是通过这样的过程，让大家切实掌握深度学习底层实现，而不是仅做一个调包侠。

本文介绍几种常用的学习率调整策略，并包含代码实现，本节内容代码实现位置 ： https://github.com/nlp-greyfoss/metagrad/blob/master/metagrad/optim.py

神经网络优化中的挑战

我们已经了解了梯度下降法，后文还会再次总结。

图1. 只有一个参数的损失函数图像

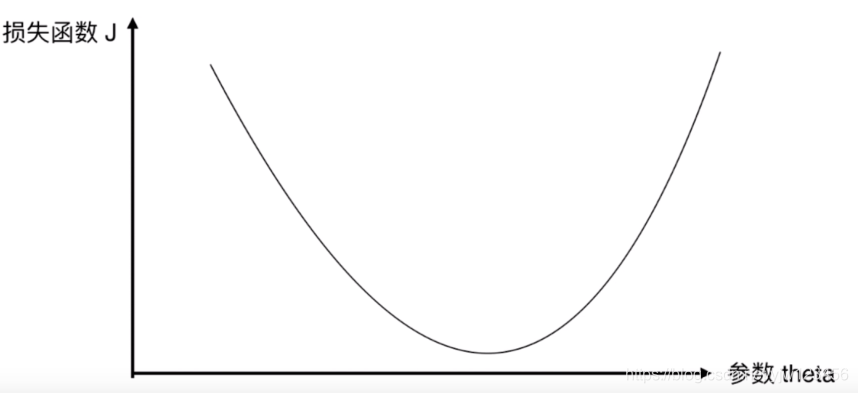
我们先来看最简单的情况，如图1，只有一个参数(和一个维度)。从损失函数的图像可以看出来这是一个凸优化问题，极小值点恰好是最小值点(全局最优解)。

图2. 学习率过小

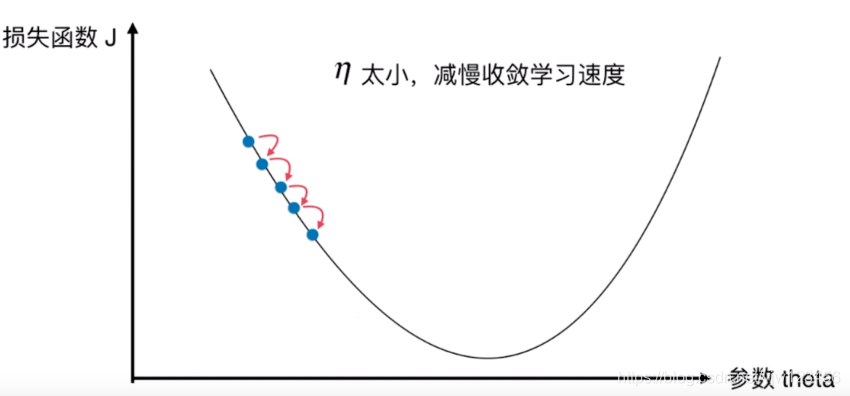
但是哪怕是这种最简单的情况下，学习率的选择也很重要。如果学习率过小，使用梯度下降法会导致收敛得非常慢。

图3. 学习率过大

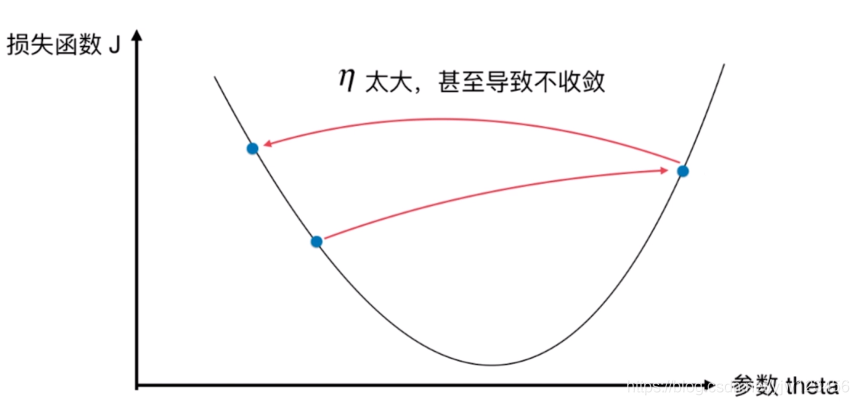
学习率过小的话还好，只是需要多花费点时间。如果学习率过大，如图3所示，在下降的时候会越过最小点，从而产生波动。这种情况会导致不收敛，浪费了时间。

图4. 全局最优解与局部最优解

通常情况下，损失函数是一个非凸问题，常见的是除了全局最优点，还有很多局部最优点。

那么，梯度下降法很有可能找到的是局部最优点，而不是全局最优点。那么如何逃离局部最优点，下面会介绍的一种方法是引入“惯性”，让它继续冲一波，从而有机会落在全局最优点。

但通常我们的神经网络接收的输入都是多维的，并且隐藏层向量也是多维的，我们一般遇到的都是非凸问题，此时碰到的挑战复杂。

高维空间的非凸优化

深度神经网络的参数非常多，它的参数学习是在非常高维空间中的非凸优化问题。

在高维空间中，非凸优化问题的难点通常不在于如何逃离局部最优点，而是如何逃离鞍点(Saddle Point)。

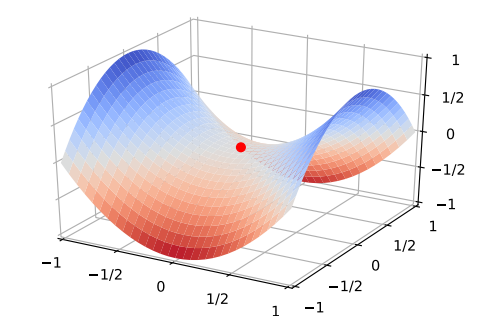
image-20230318183350696

图5. 鞍点示例(图片来源：神经网络与深度学习)

鞍点处的梯度为0，这样梯度下降法可能会在此处停止。如图1所示，鞍点在一些维度上是最高点，在另一些维度上是最低点。在高维空间中，梯度下降法更可能会困在鞍点处，而不是局部最优点。此时需要在梯度方向上引入随机性来逃离鞍点。

深度神经网络的参数非常多，并且具有一定的冗余性，使得每单个参数对最终损失的影响都比较小，因此会导致损失函数在局部最小点附近通常是一个平坦的区域，称为平坦最小值。图6给出了平坦最小值和尖锐最小值的示例。

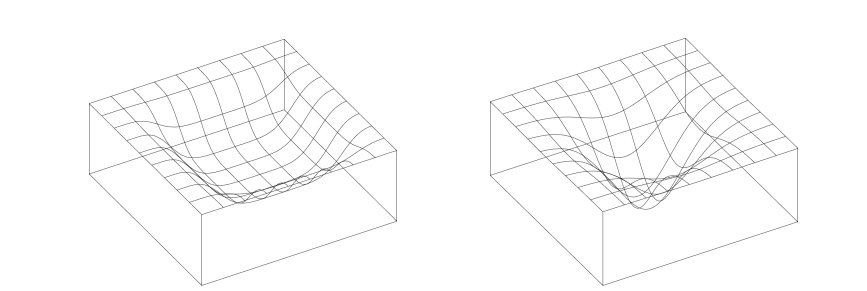
image-20230318191116831

图6. 左：平坦最小值 右：尖锐最小值(图片来源：神经网络与深度学习)

在一个平坦最小值的邻域内，所有点对应的训练损失都比较接近。这个平坦最小值通常被认为和模型泛化能力有一定的关系，一般当模型收敛到一个平坦的局部最小值时，其鲁棒性会更好，即泛化能力好。而当模型收敛到一个尖锐的局部最小值时，其鲁棒性会比较差。

在非常大的神经网络里，大部分的局部最小解是等价的。虽然神经网络有一定的概率收敛于比较差的局部最小值，但随着网络规模的增加，这种概率大大降低。因此，在训练神经网络时，我们通常没有必要找全局最小值，这样反而可能会导致过拟合。

优化方法

改善神经网络优化的目标是找到更好的局部最小值以及提高优化效率。我们本文关心的重点是如何使用更好的优化方法来提高梯度下降法的效率以及稳定性。主要包含动态地调整学习率、梯度估计修正这两种类别。

还有使用更好的参数初始化方法，以及其他的方法后面再一起了解。

梯度下降法

有三个梯度下降法的变体，主要区别在于使用多大的数据量来计算目标函数的梯度。但是最常用的是小批量梯度下降法，如果不加说明的话，别人说随机梯度下降法(SGD)通常就是在说小批量梯度下降。

批量梯度下降

在整个数据集上为参数 θ \theta θ计算梯度：
g ← ∇ θ L ( f ( x ; θ ) , y ) θ ← ϵ g (1) \begin{aligned} g &\leftarrow \nabla_\theta L(f(\pmb x;\theta), y) \\ \theta &\leftarrow \epsilon g \end{aligned} \tag 1 gθ​←∇θ​L(f(x;θ),y)←ϵg​(1)
这里 θ \theta θ代表模型中的参数； x \pmb x x表示整个训练集； y y y是所有训练样本对应的标签； f ( ⋅ ) f(\cdot) f(⋅)是模型； ϵ \epsilon ϵ是学习率； L L L为损失函数； ∇ θ \nabla_\theta ∇θ​为对参数的梯度。

基本的梯度下降法每次使用所有训练样本的平均损失来更新参数。由于是在整个数据集上计算梯度，所以这种方法非常耗时。甚至有可能我们无法一次加载整个数据集到内存中。因此，一般不常使用。

随机梯度下降

随机梯度下降法(Stochastic gradient descent,SGD)与批量梯度下降法相反，它每次为训练集中随机选择的一个样本 x ( i ) \pmb x^{(i)} x(i)计算梯度，然后更新
g ← ∇ θ L ( f ( x ( i ) ; θ ) , y ( i ) ) θ ← ϵ g (2) \begin{aligned} g &\leftarrow \nabla_\theta L(f(\pmb x^{(i)};\theta), y^{(i)}) \\ \theta &\leftarrow \epsilon g \end{aligned} \tag 2 gθ​←∇θ​L(f(x(i);θ),y(i))←ϵg​(2)
随机梯度下降法一次更新一个样本，因此它可以快速更新且适用于在线学习。批量梯度下降法可以每次偶读朝着最优点的方向逼近，而随机梯度下降法由于每次只使用一个样本，会使得优化过程非常不稳定，每次更新时会产生波动(如图7所示)，在最优点附近震荡。

图7. 随机梯度下降法的波动(图片来源：维基百科)

小批量梯度下降

基于以上两个方法的不足，不难想到，我们可以取一个折中。就是小批量梯度下降( Mini-batch gradient descent)，每次随机使用 m m m个样本的损失来估计平均损失：
g ← 1 m ∇ θ ∑ i L ( f ( x ( i ) ; θ ) , y ( i ) ) θ ← ϵ g (3) \begin{aligned} g &\leftarrow \frac{1}{m}\nabla_\theta \sum_i L(f(\pmb x^{(i)};\theta), y^{(i)}) \\ \theta &\leftarrow \epsilon g \end{aligned} \tag 3 gθ​←m1​∇θ​i∑​L(f(x(i);θ),y(i))←ϵg​(3)
其中 m m m就是我们选择的批量大小(batch size)。

在《深度学习》中关于小批量梯度下降法的描述如下：

图8.小批量梯度下降法的描述 (图片来源：深度学习)

在训练深度神经网络时，训练数据的规模往往非常大，几乎不可能每次计算整个数据集上的梯度。遗传你，在训练深度神经网络时，经常使用小批量梯度下降法。因为它被使用的如此广泛，没有明确说明的情况下，随机梯度下降法(SGD)就是指小批量梯度下降法。我们后面介绍的优化算法基本也是基于这种小批量的形式，因此我们来仔细看下这个算法。

从上面的公式可以看到，影响小批量梯度下降法的主要因素有：

  1. 批量大小
  2. 学习率
  3. 梯度估计

梯度估计就是说我们用这个批次内样本的平均梯度 g g g来估计整个数据集上的平均梯度，以进行参数更新。

在标准的小批量梯度下降法的基础上，一些改进方法都是基于以上三个方面来做的。比如如何选择批量大小、如何动态地调整学习率以及如何修正梯度估计。我们也从这三个方面来介绍常用的优化方法。

批量大小的选择

在小批量梯度下降法中，批量大小对网络优化的影响也非常大。一般来说，批量大小不影响随机梯度的期望，但会影响随机梯度的方法。批量大小越大，随机梯度的方差就越小，引入的噪声也越小，训练也越稳定，此时可以设置较大的学习率；而当批量大小较小时，需要设置较小的学习率，否则模型会不收敛。

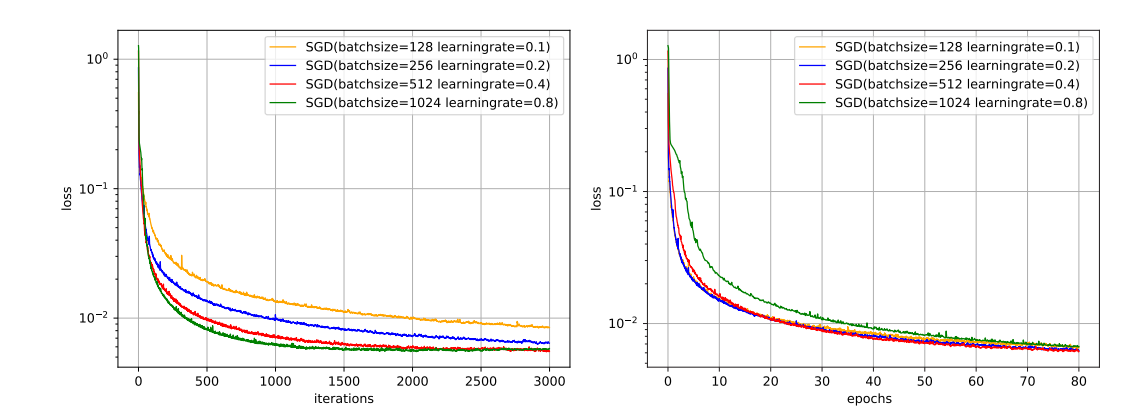
image-20230319104532264

图9.批量大小对损失下降的影响 (图片来源：神经网络与深度学习)

图8给出了从回合(epoch)和迭代(iteration)的角度来看批量大小对损失下降的影响。每一次小批量更新为一次迭代，所有训练集的样本更新一遍为一个epoch，两者的关系为：
epoch = ( N m ) × iteration \text{epoch} = \left( \frac{N}{m} \right) \times \text{iteration} epoch=(mN​)×iteration
N N N是训练样本的总数； m m m是小批量大小。

但注意由于上图中四种批量大小对应的学习率设置不同，因此并不是严格的对比。

从上图左可以看出，批量大小越大，下降效果越明显，同时下降曲线也越平滑。但从上图右可以看出，如果按整个数据集上的epoch来看的话，则是批量大小越小，下降效果越明显，适当小的批量会导致更快的收敛。

批量越大，越可能收敛到尖锐最小值，从而可能过拟合；而批量越小，越可能收敛到平坦最小值，泛化能力更好。

下面我们来看学习率的调整。

学习率调整

我们已经在上文中看到了学习率的取值很重要，但同样重要的是学习率也不能一成不变。在训练开始阶段的学习率可以设大一点，而在训练的结束阶段，此时梯度相对较小，为了防止在最优点附近波动，学习率应该设小一点。但人工调整学习率的方法不灵活，因此常用的是自动的自适应的调整方法，比如下文要介绍的AdaGrad、RMSprop、AdaDelta等。

学习率衰减

为了做到一开始学习率大一些，在后面最优点附近学习率小些。比较简单的方法是通过学习率衰减(Learning Rate Decay)的方式来实现。

指数衰减

把学习率按指数形式衰减是常用的策略，在每个epoch对学习率以参数衰减率gamma进行衰减：
l r epoch = G a m m a ∗ l r epoch-1 lr_\text{epoch} = Gamma * lr_\text{epoch-1} lrepoch​=Gamma∗lrepoch-1​
注意，这里是每个epoch后才去衰减学习率。gamma是一个小于1的小数。

由于这是我们遇到的第一个学习率衰减方法，这里详细解释一下，假设gamma=0.7：

第一次迭代，学习率 l r = 0. 7 0 ∗ l r init lr=0.7^0 * lr_\text{init} lr=0.70∗lrinit​， l r init lr_\text{init} lrinit​为设定的初始学习率；

第二次迭代，学习率 l r = 0. 7 1 ∗ l r init lr=0.7^1 * lr_\text{init} lr=0.71∗lrinit​；

第二次迭代，学习率 l r = 0. 7 2 ∗ l r init lr=0.7^2 * lr_\text{init} lr=0.72∗lrinit​；

…

同时我们参照Pytorch实现基于epoch数量的调整学习率方法。

首先定义一个学习率控制器：

class LRScheduler:
    def __init__(self, optimizer: Optimizer, last_epoch: int = -1, verbose: bool = False):
        
        self.optimizer = optimizer
        if last_epoch == -1:
            for group in optimizer.param_groups:
                group.setdefault("initial_lr", group["lr"])
        else:
            for i, group in enumerate(optimizer.param_groups):
                if 'initial_lr' not in group:
                    raise KeyError(f"param 'initial_lr' is not specified "
                                   "in param_groups[{i}] when resuming an optimizer")

        self.base_lrs = [group["initial_lr"] for group in optimizer.param_groups]
        self.last_epoch = last_epoch
        self.verbose = verbose
        self._initial_step()

    def get_lr(self):
        return NotImplementedError

    def get_last_lr(self):
        return self._last_lr

    def print_lr(self, is_verbose, group, lr, epoch=None):
        """如果 is_verbose为True， 打印当前的学习率"""
        if is_verbose:
            if epoch is None:
                print(f"Adjusting learning rate of group {group} to {lr:.4e}.")
            else:
                epoch_str = ("%.2f" if isinstance(epoch, float) else "%.5d") % epoch
                print(f'Epoch {epoch_str}: adjusting learning rate of group {} to {lr:.4e}.')

    def _initial_step(self):
        """初始化step count并调用一次step"""
        self.optimizer._step_count = 0  
        self._step_count = 0
        self.step()

    def step(self, epoch=None):

        self._step_count += 1

        if epoch is None:
            self.last_epoch += 1
        else:
            self.last_epoch = epoch

        for i, data in enumerate(zip(self.optimizer.param_groups, self.get_lr())):
            param_group, lr = data
            param_group["lr"] = lr # 用新的学习率覆盖当前学习率
            self.print_lr(self.verbose, i, lr, epoch)
        # 保存最近一次学习率
        self._last_lr = [group['lr'] for group in self.optimizer.param_groups]

核心代码在step()方法中，负责维护一些状态以及更新学习率。它的子类只需要实现get_lr()方法返回衰减后的学习率，这看起来像设计模式中的模板方法模式。

然后实现我们这里的指数衰减：

class ExponentialLR(LRScheduler):
    def __init__(self, optimizer, gamma, last_epoch=-1, verbose=False):
        """
        每个epoch通过gamma衰减每个parameter group的学习率，当last_epoch=-1，学习率设为初始值
        :param optimizer: 优化器
        :param gamma: 学习率衰减的乘法因子
        :param last_epoch: 最后一次epoch的索引
        :param verbose: 是否为每次更新打印信息
        """
        self.gamma = gamma
        super().__init__(optimizer, last_epoch, verbose)

    def get_lr(self):
        if self.last_epoch == 0:
            # 第一次迭代就是初始学习率
            return [group["lr"] for group in self.optimizer.param_groups]
        # 然后是当前学习率乘以gamma
        return [group["lr"] * self.gamma for group in self.optimizer.param_groups]

由于是在每次epoch后进行衰减，因此常见的学习率衰减用法如下：

optimizer = optim.SGD(model.parameters(), lr=0.01)
scheduler = ExponentialLR(optimizer, gamma=0.9)
# 假设有20个epoch
for epoch in range(20):
    for input, target in dataset:
        optimizer.zero_grad()
        output = model(input)
        loss = loss_fn(output, target)
        loss.backward()
        optimizer.step()
    # 在一个epoch完了之后才进行学习率衰减
    scheduler.step()

下面我们通过画出每个epoch后学习率的图像来感受一下它是怎么衰减的：

import matplotlib.pyplot as plt

import metagrad

model = metagrad.nn.Linear(2, 1)
optimizer = metagrad.optim.SGD(model.parameters(), lr=100)
scheduler = metagrad.optim.ExponentialLR(optimizer, gamma=0.1, verbose=True) # 打开输出

lrs = []

for i in range(10):
    optimizer.zero_grad()
    # 这里假设一次迭代完一个epoch
    optimizer.step()
    lrs.append(optimizer.param_groups[0]["lr"])
    # 学习率调整
    scheduler.step()

plt.plot(range(10), lrs)
plt.show()


Adjusting learning rate of group 0 to 1.0000e+02. # 100
Adjusting learning rate of group 0 to 1.0000e+01. # 10
Adjusting learning rate of group 0 to 1.0000e+00. # 1
Adjusting learning rate of group 0 to 1.0000e-01. # 0.1
Adjusting learning rate of group 0 to 1.0000e-02. # 0.01
Adjusting learning rate of group 0 to 1.0000e-03. # 0.001
Adjusting learning rate of group 0 to 1.0000e-04. # 0.0001
Adjusting learning rate of group 0 to 1.0000e-05. # 0.00001
Adjusting learning rate of group 0 to 1.0000e-06. # 0.000001
Adjusting learning rate of group 0 to 1.0000e-07. # 0.0000001
Adjusting learning rate of group 0 to 1.0000e-08. # 0.00000001

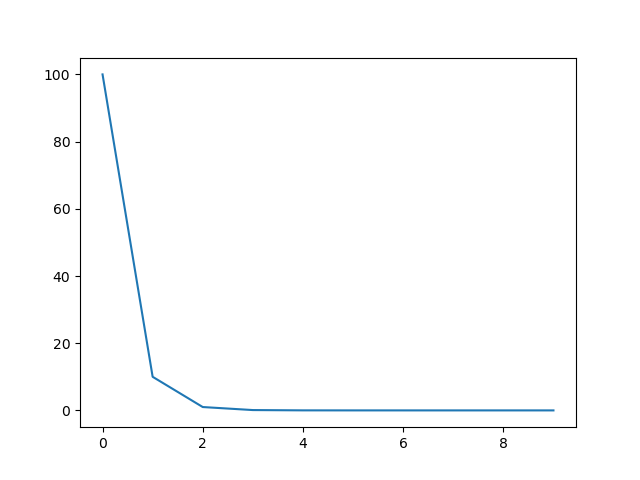
image-20230319170654679

从输出和图像可以看出，这里的学习率是以0.1的衰减率进行衰减，后面几个epoch几乎为零。

等间隔衰减

等间隔调整学习率，调整倍数为gamma倍，调整间隔为step_size，间隔单位为epoch。
l r epoch = { G a m m a ∗ l r epoch - 1 if epoch % step_size = 0 l r epoch - 1 otherwise lr_\text{epoch} = \begin{cases} Gamma * lr_{\text {epoch - 1}} & \text{if epoch \% step\_size = 0} \\ lr_{\text {epoch - 1}} & \text{otherwise} \end{cases} lrepoch​={Gamma∗lrepoch - 1​lrepoch - 1​​if epoch % step_size = 0otherwise​
如果你觉得指数衰减太快了，那么可以试试间隔衰减，它每次只会在step_size次epoch后才会进行一次衰减。

class StepLR(LRScheduler):
    def __init__(self, optimizer, step_size, gamma, last_epoch=-1, verbose=False):
        """
        每step_size个epoch通过gamma衰减每个parameter group的学习率，当last_epoch=-1，学习率设为初始值

        :param optimizer:
        :param step_size:
        :param gamma:
        :param last_epoch:
        :param verbose:
        """
        self.step_size = step_size
        self.gamma = gamma
        super().__init__(optimizer, last_epoch, verbose)

    def get_lr(self):
        if self.last_epoch == 0 or self.last_epoch % self.step_size != 0:
            # 第一次迭代或在第一个step_size间隔内
            return [group["lr"] for group in self.optimizer.param_groups]
        # 然后是当前学习率乘以gamma
        return [group["lr"] * self.gamma for group in self.optimizer.param_groups]

同样地，我们感受一下间隔衰减：

import matplotlib.pyplot as plt

import metagrad

model = metagrad.nn.Linear(2, 1)
optimizer = metagrad.optim.SGD(model.parameters(), lr=100)
scheduler = metagrad.optim.StepLR(optimizer, step_size=2, gamma=0.1, verbose=True)
lrs = []

for i in range(10):
    optimizer.zero_grad()
    optimizer.step()
    lrs.append(optimizer.param_groups[0]["lr"])
    scheduler.step()

plt.plot(range(10), lrs)
plt.show()

Adjusting learning rate of group 0 to 1.0000e+02. 
Adjusting learning rate of group 0 to 1.0000e+02.
Adjusting learning rate of group 0 to 1.0000e+01.
Adjusting learning rate of group 0 to 1.0000e+01.
Adjusting learning rate of group 0 to 1.0000e+00.
Adjusting learning rate of group 0 to 1.0000e+00.
Adjusting learning rate of group 0 to 1.0000e-01.
Adjusting learning rate of group 0 to 1.0000e-01.
Adjusting learning rate of group 0 to 1.0000e-02.
Adjusting learning rate of group 0 to 1.0000e-02.
Adjusting learning rate of group 0 to 1.0000e-03.

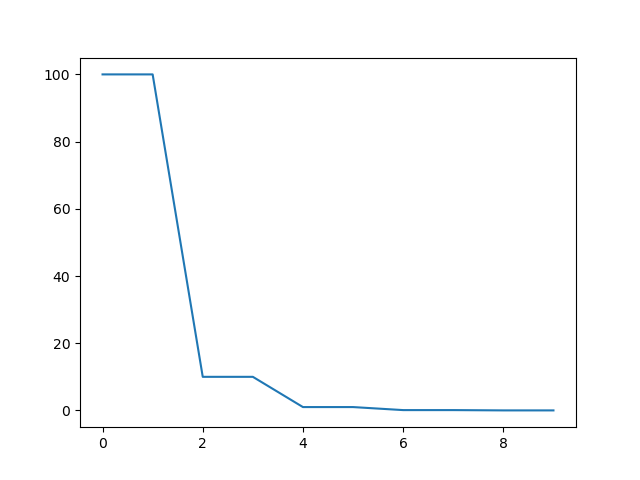
image-20230319173733610

可以看到，在一个间隔(2个epoch)内，它的学习率是一样的。

多间隔衰减

和间隔衰减类似，但学习率调整的间隔不是相等的，比如可以epoch=2时调整一次；epoch=10时调整一次；epoch=30时调整一次。这里说的这些epoch次数保存到milestones中。
l r epoch = { G a m m a ∗ l r epoch - 1 if epoch in [milestones] l r epoch - 1 otherwise lr_\text{epoch} = \begin{cases} Gamma * lr_{\text {epoch - 1}} & \text{if epoch in [milestones]} \\ lr_{\text {epoch - 1}} & \text{otherwise} \end{cases} lrepoch​={Gamma∗lrepoch - 1​lrepoch - 1​​if epoch in [milestones]otherwise​

class MultiStepLR(LRScheduler):
    def __init__(self, optimizer, milestones, gamma=0.1, last_epoch=-1, verbose=False):
        """
        一旦epoch次数达到milestones中的次数，则通过gamma衰减每个parameter group的学习率，当last_epoch=-1，学习率设为初始值

        :param optimizer:
        :param milestones: epoch索引列表，注意必须是递增的
        :param gamma:
        :param last_epoch:
        :param verbose:
        """
        self.milestones = Counter(milestones)
        self.gamma = gamma
        super().__init__(optimizer, last_epoch, verbose)

    def get_lr(self):
        if self.last_epoch not in self.milestones:
            # 如果不在milestones内，则返回当前的学习率
            return [group["lr"] for group in self.optimizer.param_groups]
        # 然后是当前学习率乘以gamma的milestones[last_epoch]次
        return [group["lr"] * self.gamma ** self.milestones[self.last_epoch] for group in self.optimizer.param_groups]

看一下它的图像：

import matplotlib.pyplot as plt

import metagrad

model = metagrad.nn.Linear(2, 1)
optimizer = metagrad.optim.SGD(model.parameters(), lr=100)
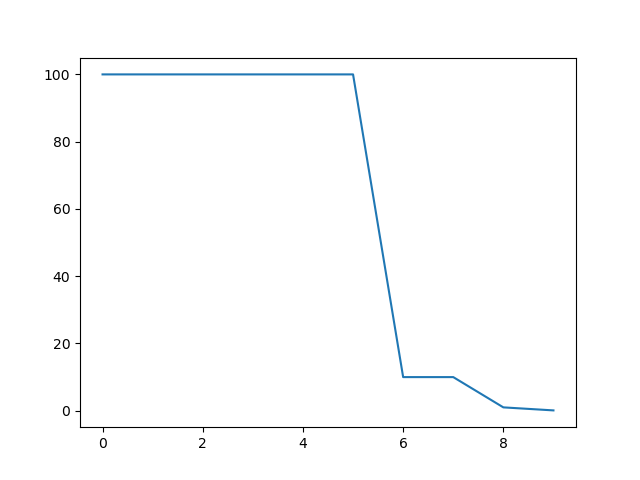
scheduler = metagrad.optim.MultiStepLR(optimizer, milestones=[6, 8, 9], gamma=0.1, verbose=True)
lrs = []

for i in range(10):
    optimizer.zero_grad()
    optimizer.step()
    lrs.append(optimizer.param_groups[0]["lr"])
    scheduler.step()

plt.plot(range(10), lrs)
plt.show()


Adjusting learning rate of group 0 to 1.0000e+02.
Adjusting learning rate of group 0 to 1.0000e+02.
Adjusting learning rate of group 0 to 1.0000e+02.
Adjusting learning rate of group 0 to 1.0000e+02.
Adjusting learning rate of group 0 to 1.0000e+02.
Adjusting learning rate of group 0 to 1.0000e+02.
Adjusting learning rate of group 0 to 1.0000e+01.
Adjusting learning rate of group 0 to 1.0000e+01.
Adjusting learning rate of group 0 to 1.0000e+00.
Adjusting learning rate of group 0 to 1.0000e-01.
Adjusting learning rate of group 0 to 1.0000e-01.

image-20230319175513042

Lambda衰减

这里的Lambda表示一个自定义函数，让初始学习率乘以该函数的返回值作为当前的学习率：
l r epoch = l r initial ∗ L a m b d a ( e p o c h ) lr_{\text {epoch}} = l r_{\text {initial}} * Lambda(epoch) lrepoch​=lrinitial​∗Lambda(epoch)

class LambdaLR(LRScheduler):
    def __init__(self, optimizer, lr_lambda, last_epoch=-1, verbose=False):
        """
        让每个parameter group的学习率为初始学习率乘以一个给定的函数lr_lambda
        :param optimizer:
        :param lr_lambda(function or list): 一个基于epoch计算乘法因子的函数；或是一个这样的函数列表，列表中每个函数
                                            对应optimizer.param_groups的每个group
        :param last_epoch:
        :param verbose:
        """
        self.optimizer = optimizer

        if not isinstance(lr_lambda, list) and not isinstance(lr_lambda, tuple):
            self.lr_lambdas = [lr_lambda] * len(optimizer.param_groups)
        else:
            # 如果是列表的话必须和param_groups的大小一致
            if len(lr_lambda) != len(optimizer.param_groups):
                raise ValueError(f"Expected {len(optimizer.param_groups)} lr_lambdas, but got {len(lr_lambda)}")
            self.lr_lambdas = list(lr_lambda)

        super().__init__(optimizer, last_epoch, verbose)

    def get_lr(self):
        return [base_lr * lmbda(self.last_epoch) for lmbda, base_lr in zip(self.lr_lambdas, self.base_lrs)]

import matplotlib.pyplot as plt

import metagrad

model = metagrad.nn.Linear(2, 1)
optimizer = metagrad.optim.SGD(model.parameters(), lr=100)

lambda1 = lambda epoch: 0.65 ** epoch
scheduler = metagrad.optim.LambdaLR(optimizer, lr_lambda=lambda1, verbose=True)

lrs = []

for i in range(10):
    optimizer.zero_grad()
    optimizer.step()
    lrs.append(optimizer.param_groups[0]["lr"])
    scheduler.step()

plt.plot(range(10), lrs)
plt.show()


Adjusting learning rate of group 0 to 1.0000e+02.
Adjusting learning rate of group 0 to 6.5000e+01.
Adjusting learning rate of group 0 to 4.2250e+01.
Adjusting learning rate of group 0 to 2.7463e+01.
Adjusting learning rate of group 0 to 1.7851e+01.
Adjusting learning rate of group 0 to 1.1603e+01.
Adjusting learning rate of group 0 to 7.5419e+00.
Adjusting learning rate of group 0 to 4.9022e+00.
Adjusting learning rate of group 0 to 3.1864e+00.
Adjusting learning rate of group 0 to 2.0712e+00.
Adjusting learning rate of group 0 to 1.3463e+00.

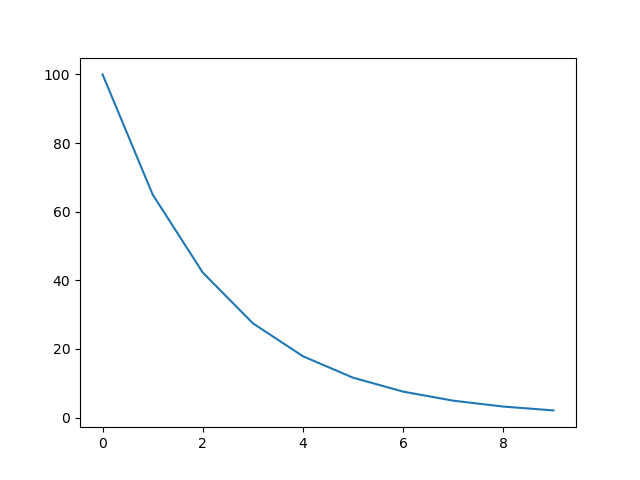
image-20230319185322009

根据指标决定学习率衰减

当某个指标在一定返回的epoch内(patience)停止提升时才进行学习率衰减，避免偶发的指标为提升导致的学习率衰减。

class ReduceLROnPlateau:
    def __int__(self, optimizer, mode="min", factor=0.1, patience=10, threshold=1e-4, threshold_mode="rel", cooldown=0,
                min_lr=0, eps=1e-8, verbose=False):
        """
        当某个指标在一定返回的epoch内(patience)停止提升时才进行学习率衰减，避免偶发的指标为提升导致的学习率衰减
        Args:
            optimizer:
            mode: min|max，指标是越小越好，还是越大越好
            factor: 衰减的乘法因子 < 1
            patience: 能容忍多少次指标不提升
            threshold: 至少提升了threshold才认为是真的提升，默认为1e-4
            threshold_mode: rel|abs。在rel模式下，max方式下dynamic_threshold = best * ( 1 + threshold )，
                                                min方式下，dynamic_threshold = best * ( 1 - threshold )；
                                     在abs模式下，max方式下dynamic_threshold = best + threshold，
                                                min方式下dynamic_threshold = best - threshold。

            cooldown: 进行一次学习率衰减后，多少个epoch内不继续衰减
            min_lr: 学习率的最小下限
            eps: 学习率的最小衰减值，如果衰减前后学习率的差值小于eps，那么就不进行更新
            verbose:

        Returns:

        """

        if factor >= 1.0:
            raise ValueError('Factor should be < 1.0.')
        self.factor = factor

        self.optimizer = optimizer
        if isinstance(min_lr, (list, tuple)):
            if len(min_lr) != len(optimizer.param_groups):
                raise ValueError(f"expected {len(optimizer.param_groups)} min_lrs, got {len(min_lr)}")
            self.min_lrs = list(min_lr)
        else:
            self.min_lrs = [min_lr] * len(optimizer.param_groups)

        self.patience = patience
        self.verbose = verbose
        self.cooldown = cooldown
        self.cooldown_counter = 0
        self.mode = mode
        self.threshold = threshold
        self.threshold_mode = threshold_mode
        self.best = None
        self.num_bad_epochs = None
        self.mode_worse = None  # 选定mode的更差的值
        self.eps = eps
        self.last_epoch = 0
        self._init_is_better(mode=mode, threshold=threshold, threshold_mode=threshold_mode)
        self._reset()

    def _reset(self):
        self.best = self.mode_worse
        self.cooldown_counter = 0
        self.num_bad_epochs = 0

    def step(self, metrics, epoch=None):
        current = float(metrics)
        if epoch is None:
            epoch = self.last_epoch + 1

        self.last_epoch = epoch

        # 如果当期指标比最佳的好
        if self.is_better(current, self.best):
            self.best = current
            self.num_bad_epochs = 0
        else:
            self.num_bad_epochs += 1

        # 在cooldown_counter > 0时不会进行衰减
        if self.in_cooldown:
            self.cooldown_counter -= 1
            self.num_bad_epochs = 0  # 在cooldown期间内num_bad_epoch一直为0

        if self.num_bad_epochs > self.patience:
            # 如果差的epoch次数大于容忍的次数，则进行学习率衰减
            self._reduce_lr(epoch)
            self.cooldown_counter = self.cooldown # 进入cooldown期间
            self.num_bad_epochs = 0 # 重置为0

        self._last_lr = [group["lr"] for group in self.optimizer.param_groups]

    def _reduce_lr(self, epoch):
        for i, param_group in enumerate(self.optimizer.param_groups):
            old_lr = float(param_group["lr"])
            # 设定新的学习率，但不能小于预设的最小学习率
            new_lr = max(old_lr * self.factor, self.min_lrs[i])
            # 如果new_lr确实减少了
            if old_lr - new_lr > self.eps:
                param_group["lr"] = new_lr
                if self.verbose:
                    epoch_str = (f"{epoch:.2f}" if isinstance(epoch, float) else f"{epoch:.5d}")
                    print(f"Epoch {epoch_str}: reducing learning rate  of group {i} to {new_lr:.4e}.")

    @property
    def in_cooldown(self):
        return self.cooldown_counter > 0

    def is_better(self, a, best):
        """ 判断a是否比best要好"""
        if self.mode == "min" and self.threshold_mode == "rel":
            rel_epsilon = 1 - self.threshold
            return a < best * rel_epsilon

        elif self.mode == "min" and self.threshold_mode == "abs":
            return a < best - self.threshold

        elif self.mode == "max" and self.threshold_mode == "rel":
            rel_epsilon = self.threshold + 1.
            return a > best * rel_epsilon

        else:  # mode == "max" and epsilon_mode == "abs":
            return a > best + self.threshold

    def _init_is_better(self, mode, threshold, threshold_mode):
        if mode not in {'min', 'max'}:
            raise ValueError('mode ' + mode + ' is unknown!')
        if threshold_mode not in {'rel', 'abs'}:
            raise ValueError('threshold mode ' + threshold_mode + ' is unknown!')

        if mode == 'min':
            self.mode_worse = float('inf')
        else:  # mode == 'max':
            self.mode_worse = -float('inf')

        self.mode = mode
        self.threshold = threshold
        self.threshold_mode = threshold_mode

它的使用方法如下：

optimizer = SGD(model.parameters(), lr=0.1)
scheduler = ReduceLROnPlateau(optimizer, 'min')
for epoch in range(10):
    train(...) # 训练
    val_loss = validate(...) # 计算验证集损失
    # 然后传入损失，决定是否需要学习率衰减
    scheduler.step(val_loss)

周期性学习率调整

为了能让梯度下降法可以逃离鞍点后尖锐最小值，一种方式是在训练过程中周期性地增大学习率。当参数处于尖锐最小值附近时，增大学习率有助于逃离尖锐最小值；当参数处于平坦最小值附近时，增大学习依然有可能在该平坦区域内。因此，周期性地增大学习率从长期来看有助于找到更好的局部最优解。

余弦退火衰减

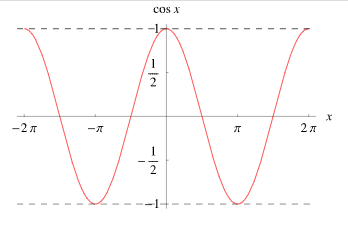
image-20230320111321215

图10.余弦函数图像

使用余弦曲线来调整学习率，首先回顾下余弦曲线，如上图10所示。在 [ 0 , π ] [0,\pi] [0,π]内，余弦曲线是逐渐下降的，从 1 1 1下降到 − 1 -1 −1。

余弦退火衰减的公式为：
η t = η min ⁡ + 1 2 ( η max ⁡ − η min ⁡ ) ( 1 + cos ⁡ ( T c u r T max ⁡ π ) ) \eta_{t}=\eta_{\min }+\frac{1}{2}\left(\eta_{\max }-\eta_{\min }\right)\left(1+\cos \left(\frac{T_{c u r}}{T_{\max }} \pi\right)\right) ηt​=ηmin​+21​(ηmax​−ηmin​)(1+cos(Tmax​Tcur​​π))
由SGDR: Stochastic Gradient Descent with Warm Restarts提出，但这里仅实现余弦退火部分，并不包含热重启部分。

其中 η t \eta_{t} ηt​表示第 t t t个epoch的学习率； η min ⁡ \eta_{\min } ηmin​表示最小学习率； η max ⁡ \eta_{\max} ηmax​表示初始学习率； T c u r T_{cur} Tcur​表示当前epoch数； T max ⁡ T_{\max} Tmax​表示总epoch数；

从公式可以看出，其中 η max ⁡ − η min ⁡ \eta_{\max }-\eta_{\min } ηmax​−ηmin​是固定的，变化处在于 cos ⁡ ( ⋅ ) \cos(\cdot) cos(⋅)中。而在 [ 0 , π ] [0,\pi] [0,π]内， cos ⁡ \cos cos函数式单调递减的。

训练刚开始时， T c u r = 0 , η t = η m a x T_{cur}=0,\eta_t = \eta_{max} Tcur​=0,ηt​=ηmax​；随着训练的进行， T c u r T_{cur} Tcur​增大， c o s ( ⋅ ) cos(\cdot) cos(⋅)减小， η t \eta_t ηt​也随着减小；当训练快结束时， T c u r T_{cur} Tcur​接近 T m a x T_{max} Tmax​， η t \eta_t ηt​则接近于 η m i n \eta_{min} ηmin​。

class CosineAnnealingLR(LRScheduler):
    def __init__(self, optimizer, T_max, eta_min=0, last_epoch=-1, verbose=False):
        """
        由SGDR提出，但这里仅实现余弦退火部分，并不包含热重启部分。
        Args:
            optimizer:
            T_max: 最多迭代次数
            eta_min: 最小学习率
            last_epoch:
            verbose:
        """
        self.T_max = T_max
        self.eta_min = eta_min
        super().__init__(optimizer, last_epoch, verbose)

    def get_lr(self):
        if self.last_epoch == 0:
            # 刚开始时，学习率最大，为默认的学习率
            return [group['lr'] for group in self.optimizer.param_groups]

        return [self.eta_min + (base_lr - self.eta_min) * (1 + math.cos(self.last_epoch * math.pi / self.T_max)) / 2 for
                base_lr in self.base_lrs]

import matplotlib.pyplot as plt

import metagrad

model = metagrad.nn.Linear(2, 1)
optimizer = metagrad.optim.SGD(model.parameters(), lr=100)
scheduler = metagrad.optim.CosineAnnealingLR(optimizer, T_max=10, eta_min=0)

lrs = []

for i in range(100):
    optimizer.zero_grad()
    optimizer.step()
    lrs.append(optimizer.param_groups[0]["lr"])
    scheduler.step()

plt.plot(lrs)
plt.show()

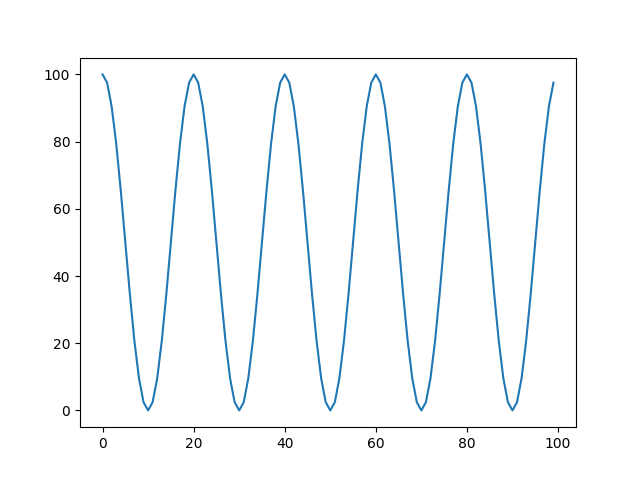
image-20230320133128306

可以看到，如果令T_max=10，同时将总epoch数设成超过它的一个数，比如100。我们可以看到它的图像实际上是一个周期性地调整。当epoch数等于20时，又回到了初始学习率，而不是在epoch数等于11的时候。

带热重启的余弦退火衰减

使用余弦退火衰减调整每个参数组的学习率，并在 T i T_i Ti​次epoch后进行热重启：
η t = η min ⁡ + 1 2 ( η max ⁡ − η min ⁡ ) ( 1 + cos ⁡ ( T cur ⁡ T i π ) ) \eta_{t}=\eta_{\min }+\frac{1}{2}\left(\eta_{\max }-\eta_{\min }\right)\left(1+\cos \left(\frac{T_{\operatorname{cur}}}{T_{i}} \pi\right)\right) ηt​=ηmin​+21​(ηmax​−ηmin​)(1+cos(Ti​Tcur​​π))
这里所谓的热重启指学习率每间隔一定周期后重新初始化为某个预先设定值，然后逐渐衰减。每次重启后模型参数不是从头开始优化，而是从重启前的参数基础上继续优化。重启周期 T i T_i Ti​可以随着重启次数逐渐增加，比如 T i = T i − 1 × k , k ≥ 1 T_i= T_{i-1} \times k,\quad k \geq 1 Ti​=Ti−1​×k,k≥1。

class CosineAnnealingWarmRestarts(LRScheduler):
    def __init__(self, optimizer, T_0, T_mult=1, eta_min=0, last_epoch=-1, verbose=False):
        """
        使用余弦退火衰减调整每个参数组的学习率，并在T_i次epoch后进行热重启，重启为初始学习率。
        T_i是两次热重启之间的间隔epoch次数。
        Args:
            optimizer:
            T_0: 第一次重启的epoch次数
            T_mult: 重启周期增大因子， ≥ 1
            eta_min: 最小学习率
            last_epoch:
            verbose:
        """
        self.T_0 = T_0
        self.T_i = T_0  # 初始T_i 为 T_0 ，后面可能会增大
        self.T_mult = T_mult
        self.eta_min = eta_min
        self.T_cur = last_epoch  # 当前间隔内的epoch次数
        super().__init__(optimizer, last_epoch, verbose)

    def get_lr(self):
        return [self.eta_min + (base_lr - self.eta_min) * (1 + math.cos(self.T_cur * math.pi / self.T_i)) / 2 for
                base_lr in self.base_lrs]

    def step(self, epoch=None):
        """这里需要重写step，在里面更新T_i和T_cur"""
        if epoch is None and self.last_epoch < 0:
            epoch = 0

        if epoch is None:
            epoch = self.last_epoch + 1
            self.T_cur = self.T_cur + 1
            if self.T_cur > self.T_i:
                self.T_cur = self.T_cur - self.T_i
                self.T_i = self.T_i * self.T_mult  # 重启次数乘以增大因子
        else:
            if epoch < 0:
                raise ValueError(f"Expected non-negative epoch, but got {epoch}")
            if epoch >= self.T_0:
                # 如果增大因子为1，即不增大
                if self.T_mult == 1:
                    self.T_cur = epoch % self.T_0
                else:
                    # 计算当前是第几次周期内，T_i为当期周期的大小
                    # 假设T_0=8;T_mul=2;
                    # 那么0-7属于第一次周期，该周期大小为8，epoch=0属于第一次周期的开始(更新T_cur=0)；
                    # 那么8-23属于第二次周期，该周期大小为16，epoch=24属于第二次周期的开始(更新T_cur=0)；
                    # T_cur是当期周期内的epoch数
                    n = int(math.log((epoch / self.T_0 * (self.T_mult - 1) + 1), self.T_mult))
                    # 更新当前周期内的epoch数
                    self.T_cur = epoch - self.T_0 * (self.T_mult ** n - 1) / (self.T_mult - 1)
                    # 计算周期大小
                    self.T_i = self.T_0 * self.T_mult ** n
            else:
                # 如果还在第一个周期内
                self.T_i = self.T_0
                self.T_cur = epoch

        self.last_epoch = math.floor(epoch)

        for i, data in enumerate(zip(self.optimizer.param_groups, self.get_lr())):
            param_group, lr = data
            param_group["lr"] = lr
            self.print_lr(self.verbose, lr, epoch)

        self._last_lr = [group['lr'] for group in self.optimizer.param_groups]

import matplotlib.pyplot as plt

import metagrad

model = metagrad.nn.Linear(2, 1)
optimizer = metagrad.optim.SGD(model.parameters(), lr=0.1)
scheduler = metagrad.optim.CosineAnnealingWarmRestarts(optimizer, T_0=8, T_mult=2, eta_min=0.001, last_epoch=-1)

lrs = []

for i in range(248):
    optimizer.zero_grad()
    optimizer.step()
    lrs.append(optimizer.param_groups[0]["lr"])
    scheduler.step()

plt.plot(lrs)
plt.show()

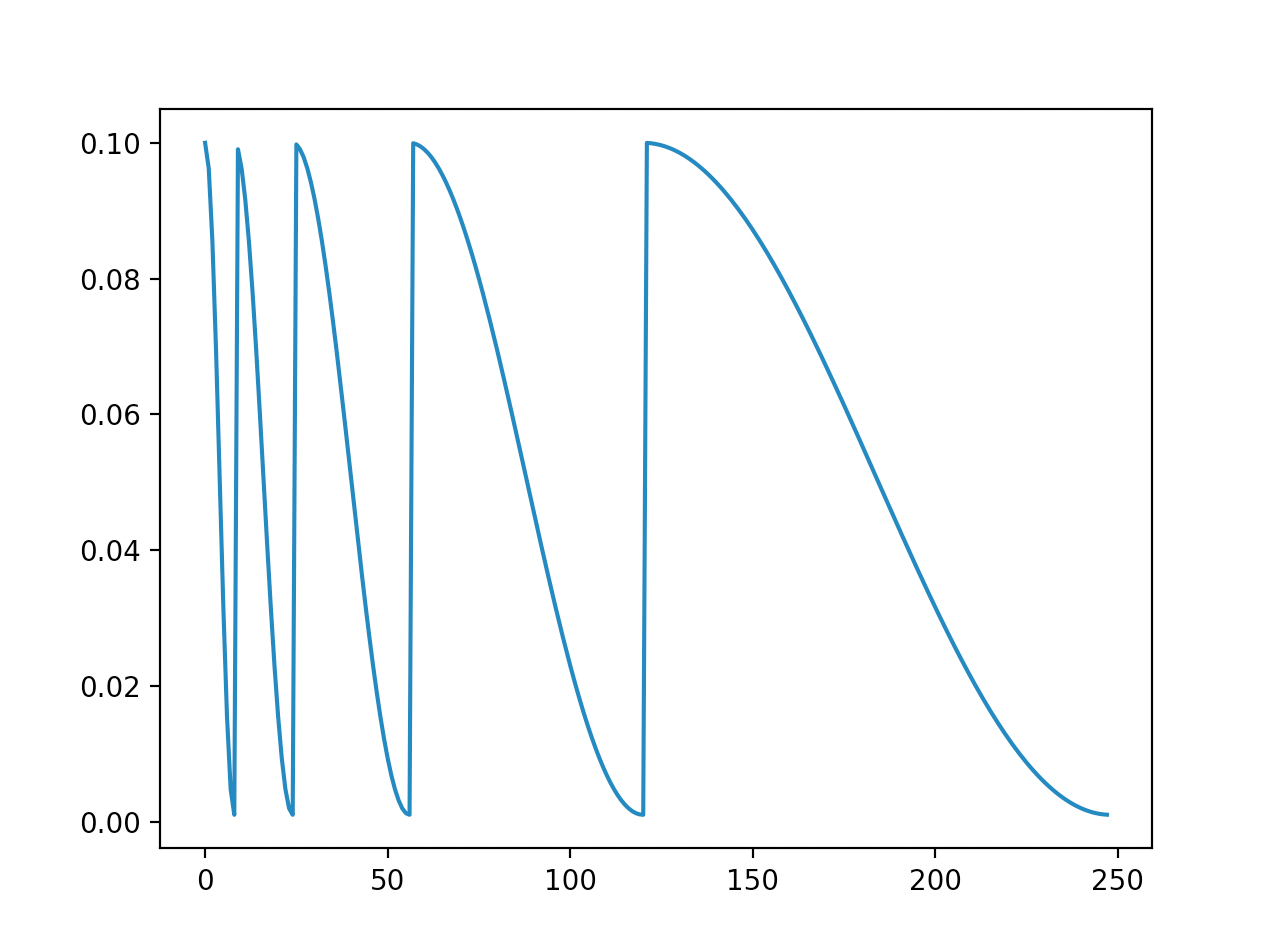
image-20230320191443067

如上图，可以看到学习率在第一次周期大小8内从0.1下降到了0.001；在第二次周期的开始又恢复最大值，然后在第23次epoch时达到最低值；

学习率的更新间隔越来越大。

学习率预热

在小批量梯度下降法中，当批量大小的设置比较大时，通常需要比较大的学习率。但在刚开始训练时，由于参数是随机初始化的，梯度往往比较大，而此时的学习率也较大，会使训练不稳定。

为了提高训练的稳定性，可以在最初几轮迭代时，采用比较小的学习率，等梯度下降到一定程度后再恢复到初始的学习率，这种方法称为学习率预热(Learning Rate Warmup)。

NoamLR

这里我们实现Transformer中提出的学习率预热方法：
l r a t e = d model − 0.5 ⋅ min ⁡ ( s t e p _ n u m − 0.5 , s t e p _ n u m ⋅ w a r m u p _ s t e p s − 1.5 ) lrate = d_{\text{model}}^{-0.5} \cdot \min({step\_num}^{-0.5}, {step\_num} \cdot {warmup\_steps}^{-1.5}) lrate=dmodel−0.5​⋅min(step_num−0.5,step_num⋅warmup_steps−1.5)
参考文章： http://nlp.seas.harvard.edu/annotated-transformer 实现。

class NoamLR(LRScheduler):
    def __init__(self, optimizer, model_size, factor=1., warmup_steps=4000, last_epoch=-1, verbose=False):
        """
        参考 http://nlp.seas.harvard.edu/annotated-transformer 实现的Transformer提出的学习率衰减方法
        在第一个warmup_steps内线性地增大学习率，然后按步长的平方倒数成比例地减小
        :param optimizer: 优化器
        :param model_size: 模型嵌入层大小
        :param factor: 乘法因子
        :param warmup_steps: 加热步
        :param last_epoch:
        :param verbose:
        """
        self.optimizer = optimizer
        self.warmup_steps = warmup_steps
        self.model_size = model_size
        self.factor = factor

        super().__init__(optimizer, last_epoch, verbose)

    def get_lr(self):
        # 避免0的负幂次
        if self.last_epoch == 0:
            self.last_epoch = 1

        step = self.last_epoch
        lr = self.factor * (self.model_size ** (-0.5) * min(step ** (-0.5), step * self.warmup_steps ** (-1.5)))
        return [lr] * len(self.optimizer.param_groups)

import matplotlib.pyplot as plt

import metagrad

model = metagrad.nn.Linear(2, 1)
optimizer = metagrad.optim.SGD(model.parameters(), lr=100)

scheduler = metagrad.optim.NoamLR(optimizer, 512)

lrs = []

for i in range(20000):
    optimizer.zero_grad()
    optimizer.step()
    lrs.append(optimizer.param_groups[0]["lr"])
    scheduler.step()

plt.plot(range(20000), lrs)
plt.show()

image-20230320132442220

参考

  1. 神经网络与深度学习
  2. 深度学习
  3. Pytorch
  4. Guide to Pytorch Learning Rate Scheduling

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/496510.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

day24_多线程

day24_多线程

今日内容 零、 复习昨日 一、作业 二、线程安全的集合 三、死锁 四、线程通信 五、生产者消费者 六、线程池 零、 复习昨日 见晨考 一、作业 售卖后车票 见代码二、线程安全的类[了解] StringBuffer是线程安全的,是因为每个方法都加上synchronized,即都是同步方法 StringBuil…
阅读更多...
【前端】前后端分离ruoyi-vue初步学习

【前端】前后端分离ruoyi-vue初步学习

1.了解vue基础知识。 Vue.js - 渐进式 JavaScript 框架 | Vue.js (vuejs.org) 2.将ruoyi-vue项目拉下来&#xff0c;并成功运行。 开源项目网址&#xff1a;RuoYi 若依官方网站 |后台管理系统|权限管理系统|快速开发框架|企业管理系统|开源框架|微服务框架|前后端分离框架|…
阅读更多...
《Netty》从零开始学netty源码（五十四）之PoolThreadLocalCache

《Netty》从零开始学netty源码（五十四）之PoolThreadLocalCache

PoolThreadLocalCache 前面讲到PoolThreadCache&#xff0c;它为线程提供内存缓存&#xff0c;当线程需要分配内存时可快速从其中获取&#xff0c;在Netty中用PoolThreadLocalCache来管理PoolThreadCache&#xff0c;它的数据结构如下&#xff1a; PoolThreadLocalCache相当…
阅读更多...
【网络】UDP网络服务器简单模拟实现

【网络】UDP网络服务器简单模拟实现

【网络】UDP网络服务器简单模拟实现 文章目录 makefile服务端udpServerudpServer.ccudpServer.hpp初始化启动测试 客户端udpClientudpClient.ccudpClient.hpp初始化启动 整体代码 UDP的封装: UDP网络服务器模拟实现&#xff1a;主要分为makefile文件进行编译 UDP客户端&#xf…
阅读更多...
Java开发 - 不知道算不算详细的分布式事务详解

Java开发 - 不知道算不算详细的分布式事务详解

前言 前日对JUC进行了一个深度总结&#xff0c;不过现在博主能记得的也不多了&#xff0c;只是这东西&#xff0c;不是看几遍写几遍就能完全记住的&#xff0c;功夫在平时&#xff0c;很多知识点都需要反复的看&#xff0c;不光要看&#xff0c;还要用&#xff0c;这样才能了解…
阅读更多...
在CentOS上安装Jenkins并配置Docker

在CentOS上安装Jenkins并配置Docker

文章目录 步骤1 - 安装Java 11步骤2 - 安装Jenkins步骤3 - 安装Docker步骤4 - 配置Docker Cloud步骤 5 - 验证步骤 6 - 可能会遇到的问题 在本教程中&#xff0c;我们将展示如何在CentOS上安装Jenkins和Docker&#xff0c;并将它们配置在同一台机器上&#xff0c;使Jenkins能够…
阅读更多...
《花雕学AI》WeTab+ChatGPT：让浏览器变成你的智能助手

《花雕学AI》WeTab+ChatGPT：让浏览器变成你的智能助手

引言&#xff1a; 浏览器是我们日常使用的最重要的工具之一&#xff0c;它可以帮助我们获取信息、娱乐、学习、工作等。但是&#xff0c;传统的浏览器往往不能满足我们的个性化需求&#xff0c;也不能给我们提供智能化的服务。那么&#xff0c;有没有一种浏览器可以让我们的体…
阅读更多...
yoloV2细节改进

yoloV2细节改进

文章目录 1 v2 细节升级概述2 .网络结构特点3. 架构细节解读4. 基于聚类来选择先验框尺寸5. 偏移量计算方法6. 坐标映射与还原7 感受野8. 特征融合的改进其他知识点filter 是什么&#xff1f; 1 v2 细节升级概述 2 .网络结构特点 使用dropout&#xff0c;杀死部分神经元&#…
阅读更多...
Java集合之单列集合

Java集合之单列集合

分类 集合分为单列集合&#xff08;Collection&#xff09;和双列集合&#xff08;Map&#xff09; 单列集合的体系结构 List集合和Set集合的区别 List系列集合&#xff1a;添加元素是有序的&#xff08;添加的顺序&#xff0c;而非数据的大小顺序&#xff09;、可重复、有索引…
阅读更多...
为什么在Ubuntu系统使用附加驱动更新Nvidia显卡驱动不起作用

为什么在Ubuntu系统使用附加驱动更新Nvidia显卡驱动不起作用

1. 硬件环境 CPU&#xff1a;AMD Ryzen 9 5950x 16-core processor 32 GPU&#xff1a;双GeForce RTX 3090 操作系统&#xff1a;Ubuntu 22.04.2 LTS 64 位 主板&#xff1a;ASUS的ROG CROSSHAIR VIII EXTREME 2. 问题描述 使用上图所示的附加驱动程序更新Nvidia显卡驱动&am…
阅读更多...
恢复item2和oh-my-zsh的配置

恢复item2和oh-my-zsh的配置

1. 首先正常安装item2 2. 加载onedrive里的传家宝iterm2_default_profile.json&#xff0c;让iterm2的配置生效 2. 然后正常安装oh-my-zsh (官方步骤&#xff1a; sh -c "$(curl -fsSL https://raw.githubusercontent.com/ohmyzsh/ohmyzsh/master/tools/install.sh)&q…
阅读更多...
C# 学习abstract

C# 学习abstract

abstract 顾名思义&#xff1a;抽象 从微软官方文档来看&#xff1a;abstract 修饰符指示被修改内容的实现已丢失或不完整。 abstract 修饰符可用于类、方法、属性、索引和事件。 在类声明中使用 abstract 修饰符来指示某个类仅用作其他类的基类&#xff0c;而不用于自行进行…
阅读更多...
linux内核调试的几个方法

linux内核调试的几个方法

参考 以下内容&#xff1a; Linux 笔记&#xff1a; https://xuesong.blog.csdn.net/article/details/109522945?spm1001.2014.3001.5502 printk: printk在内核源码中用来记录日志信息的函数&#xff0c;只能在内核源码范围内使用。用法和printf非常相似&#xff1b; printk…
阅读更多...
InsCode体验报告

InsCode体验报告

文章目录 前言一、InsCode是什么&#xff1f;二、体验过程1.创建项目2.在线IDE3.运行和部署项目4.浏览和学习项目5.分享和协作项目6.支持AI助手 三、体验感受优点缺点 总结 官方宣传视频 InsCode-AI 前言 作为一个大三计算机专业的学生&#xff0c;我对编程有着浓厚的兴趣和热…
阅读更多...
Triloga 的任务 — Satta 系列来袭！

Triloga 的任务 — Satta 系列来袭！

谁战胜了这些凶兽&#xff0c;谁就获得了力量&#xff0c;让我们通过装备体现出来&#xff01;来自神秘洞穴的疯狂昆虫外壳&#xff0c;黄昏之地燃烧中的部落的骨质盔甲&#xff0c;以及深海的美妙灯光。 Triloga 的任务——Satta 系列已在 The Sandbox 市场平台上架&#xff1…
阅读更多...
JVM（类的加载与ClassLoader、双亲委派机制）

JVM（类的加载与ClassLoader、双亲委派机制）

文章目录 1. 类的生命周期2. 类的加载过程3. 类加载器&#xff08;classloader)3.1 类加载器的作用3.2 类加载器的分类(JDK8)3.3 双亲委派机制3.3.1 双亲委派机制优势 3.4 查看某个类的类加载器对象3.5 使用ClassLoader获取流 1. 类的生命周期 类在内存中完整的生命周期&#…
阅读更多...
( “ 图 “ 之 并查集 ) 684. 冗余连接 ——【Leetcode每日一题】

( “ 图 “ 之 并查集 ) 684. 冗余连接 ——【Leetcode每日一题】

❓684. 冗余连接 难度&#xff1a;中等 树可以看成是一个连通且 无环 的 无向 图。 给定往一棵 n 个节点 (节点值 1&#xff5e;n ) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间&#xff0c;且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n…
阅读更多...
基于 EKS Fargate 搭建微服务性能分析系统

基于 EKS Fargate 搭建微服务性能分析系统

背景 近期 Amazon Fargate 在中国区正式落地&#xff0c;因 Fargate 使用 Serverless 架构&#xff0c;更加适合对性能要求不敏感的服务使用&#xff0c;Pyroscope 是一款基于 Golang 开发的应用程序性能分析工具&#xff0c;Pyroscope 的服务端为无状态服务且性能要求不敏感&…
阅读更多...
Java阶段二Day14

Java阶段二Day14

Java阶段二Day14 文章目录 Java阶段二Day14复习前日知识点SpringFramework版本SpringFramework核心SpringFramework创建工程SpringFramework相关概念bean对象的创建过程xml配置文件中的标签 基于XML管理bean对象类型属性的注入数组类型属性注入集合类型属性注入p命名空间引入外…
阅读更多...
ConMask: Open-World Knowledge Graph Completion

ConMask: Open-World Knowledge Graph Completion

目录 Abstract Introduction Model Relationship-Dependent Content Masking Target Fusion Loss Function [1711.03438] Open-World Knowledge Graph Completion (arxiv.org) Abstract 引入一个名为ConMask的开放世界KGC模型&#xff0c;该模型学习实体名称和部分文本…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023