复数的基本知识
文章目录
- 复数的基本知识
- 前言
- 表示方法
- 百度百科
- 简单来说:
- 复数的运算
前言
这里只有一点点关于复数的知识,主要是最近的FFT要用到。
表示方法
百度百科
我们把形如 a+bi (a,b均为实数)的数称为复数,其中a称为实部,b称为虚部,i称为虚数单位 。当虚部等于零时,这个复数可以视为实数;当z的虚部不等于零时,实部等于零时,常称z为纯虚数。复数域是实数域的代数闭包,也即任何复系数多项式在复数域中总有根。 复数是由意大利米兰学者卡当在十六世纪首次引入,经过达朗贝尔、棣莫弗、欧拉、高斯等人的工作,此概念逐渐为数学家所接受。
简单来说:
我们定义: i 2 = − 1 i ^ 2 = -1 i2=−1 , 一个复数 z z z 可以表示为: z = a + b i ( a , b ∈ R ) z = a + b i (a , b \in R) z=a+bi(a,b∈R)
其中 a a a 为 实部 , b b b 为 **虚部 ** , i i i 为 虚数单位
比如: − 5 = 5 i \sqrt{-5} = \sqrt5\ i −5=5 i
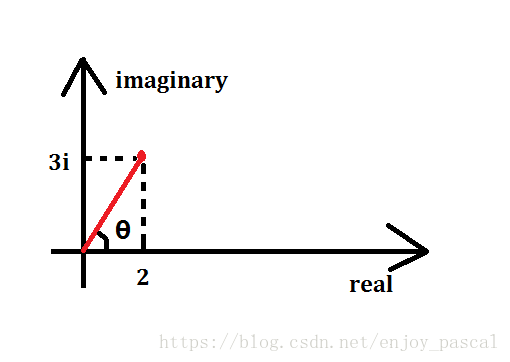
我们还可以把复数表示为 复平面 直角坐标系上的一个点,比如下面:
其中 x x x 轴表示实数, y y y 轴表示虚数。
这个点 ( 2 , 3 ) (2 , 3) (2,3) 表示的 复数 就是 2 + 3 i 2 +3 i 2+3i ,或者想象它代表的向量为 ( 2 , 3 ) (2 , 3) (2,3)
我们还可以把它表示成 ( 13 , θ ) (\sqrt{13} , θ) (13,θ)
一个复数 z = a + b i z = a + b i z=a+bi 的共轭复数为 a − b i a - bi a−bi (虚部取反)
复数的运算
复数不像点或向量,它和实数一样可以进行四则运算
复数相加满足 平行四边形法则
复数相乘满足 模长相乘,极角相加
设两个复数分别为
z
1
=
a
+
b
i
,
z
2
=
c
+
d
i
z_1 = a + bi , z_2 = c + di
z1=a+bi,z2=c+di ,那么
z
1
+
z
2
=
(
a
+
c
)
+
(
b
+
d
)
i
z
1
+
z
2
=
(
z
c
−
b
d
)
+
(
a
d
+
b
c
)
i
(
a
1
,
θ
1
)
∗
(
a
2
,
θ
2
)
=
(
a
1
a
2
,
θ
1
+
θ
2
)
z_1 + z_2 = (a + c) + (b + d)i \\ z_1 + z_2 = (zc - bd) + (ad + bc)i \\ (a_1 , θ_1) * (a_2 , θ_2) = (a_1 a_2 , θ_1 + θ_2)
z1+z2=(a+c)+(b+d)iz1+z2=(zc−bd)+(ad+bc)i(a1,θ1)∗(a2,θ2)=(a1a2,θ1+θ2)




![[MySQL / Mariadb] 数据库学习-Linux中二进制方式安装MySQL5.7](https://img-blog.csdnimg.cn/c0223722813d4283a2ec85cc7a54b9e1.png)