文章目录
- 单调栈的学习
- 什么是单调栈?
- 单调栈模板
- 暴力解法
- 单调栈解法
- 单调栈的简单变形
- 1.[496. 下一个更大元素 I](https://leetcode.cn/problems/next-greater-element-i/)
- 2.[739. 每日温度](https://leetcode.cn/problems/daily-temperatures/)
- 3.[503. 下一个更大元素 II](https://leetcode.cn/problems/next-greater-element-ii/)
- 总结
单调栈的学习
什么是单调栈?
栈(stack)是很简单的一种数据结构,先进后出的逻辑顺序,符合某些问题的特点,比如说函数调用栈。
单调栈实际上就是栈,只是利用了一些巧妙的逻辑使得每次新元素入栈后,栈内的元素都保持有序(单调递增或者单调递减)
听起来有点像堆(heap)
但是不是堆,单调栈用途不太广泛,只处理一类典型的问题
- 下一个更大元素
- 上一个更小元素
- …
单调栈模板
输入一个数组nums,请返回一个等长的结果数组,结果数组中对应索引存储着下一个更大元素,如果没有更大元素就保存-1
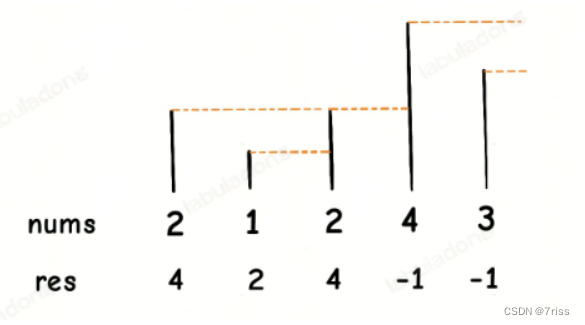
比如,输入一个数组nums=[2,1,2,4,3],返回数组[4,2,4,-1,-1]。因为第一个2后面比2大的数是4;1后面比1大的数是2;第二个2后面比2大的数是4;4后面没有比4大的数,填-1;3后面没有比3更大的数,填-1.
暴力解法
就是堆每个元素后面都进行扫描,找到第一个更大的元素就行了。但是暴力解法的时间复杂度是 O(n^2)。
单调栈解法
我们可以把这个问题抽象为:
把数组的元素想象成并列站立的人,元素大小想象成人的身高。这些人面对你站成一列,如何求元素2的下一个更大元素?
如果能够看到元素2,那么它后面可见的第一个人就是2的下一个更大元素。
为什么?
因为比2小的元素身高不够,都被2挡住了,所以第一个露出来的就是答案
如图所示:
代码实现如下:
int[] nextGreaterElement(int[] nums) {
int n = nums.length;
// 存放答案的数组
int[] res = new int[n];
Stack<Integer> s = new Stack<>();
// 倒着往栈里放
for (int i = n - 1; i >= 0; i--) {
// 判定个子高矮
while (!s.isEmpty() && s.peek() <= nums[i]) {
// 矮个起开,反正也被挡着了。。。
s.pop();
}
// nums[i] 身后的更大元素
res[i] = s.isEmpty() ? -1 : s.peek();
s.push(nums[i]);
}
return res;
}
for循环要从后往前扫描元素,因为我们借助的是栈的结构,倒着入栈其实就是正着出栈。
while循环就是把两个个子高元素之间的元素排除掉,因为它们的存在是没有意义的,前面挡着个更高的元素,所以它们不可能被作为后续进来的元素的下一个更大元素
这个算法的时间复杂度并不直观,如果看到for循环嵌套while循环,可能认为这个算法的时间复杂度也是 O(n^2),但是实际上这个算法的复杂度只有 O(n)。
因为从整体上看,总共有n个元素,每个元素都被push入栈了一次,而最多就会被pop一次,没有任何冗余操作。所以总的计算规模是和元素规模n成正比的,也就是O(n)的复杂度
单调栈的简单变形
1.496. 下一个更大元素 I
这道题就是给你输入两个数组nums1和nums2,让你求nums1中的元素在nums2中的下一个更大元素
其实很容易就可以解决这个问题,因为题目说nums1是nums2的子集,所以我们先把nums2中每个元素的下一个更大元素算出来存到一个映射里,然后让nums1中的元素去查表即可
完整代码如下:
int[] nextGreaterElement(int[] nums1, int[] nums2) {
// 记录 nums2 中每个元素的下一个更大元素
int[] greater = nextGreaterElement(nums2);
// 转化成映射:元素 x -> x 的下一个最大元素
HashMap<Integer, Integer> greaterMap = new HashMap<>();
for (int i = 0; i < nums2.length; i++) {
greaterMap.put(nums2[i], greater[i]);
}
// nums1 是 nums2 的子集,所以根据 greaterMap 可以得到结果
int[] res = new int[nums1.length];
for (int i = 0; i < nums1.length; i++) {
res[i] = greaterMap.get(nums1[i]);
}
return res;
}
int[] nextGreaterElement(int[] nums) {
// 见上文
}
或者是
class Solution {
private static Map<Integer,Integer> greaterElements;
public int[] nextGreaterElement(int[] nums1, int[] nums2) {
greaterElements(nums2);
int[] res=new int[nums1.length];
for(int i=0;i<nums1.length;i++){
res[i]=greaterElements.get(nums1[i]);
}
return res;
}
public static void greaterElements(int[] nums){
greaterElements=new HashMap<>();
Stack<Integer> stack=new Stack<>();
for(int i=nums.length-1;i>=0;i--){
while(!stack.isEmpty()&&nums[i]>=stack.peek()){
stack.pop();
}
if(stack.isEmpty()){
greaterElements.put(nums[i],-1);
}else{
greaterElements.put(nums[i],stack.peek());
}
stack.push(nums[i]);
}
}
}
2.739. 每日温度
给你一个温度数组temperatures,这个数组存放的是近几天的天气温度,题目要求返回一个等长的数组,计算对于每一天你还至少要等多少天才能等到一个更暖和的气温,如果等不到那一天填0
比如说给你输入
temperatures = [73,74,75,71,69,76],你返回[1,1,3,2,1,0]。因为第一天 73 华氏度,第二天 74 华氏度,比 73 大,所以对于第一天,只要等一天就能等到一个更暖和的气温,后面的同理。这个问题本质上也是找下一个更大的元素,只不过现在不是问下一个更大的元素的值是多少,而是问你当前元素距离下一个更大元素的索引距离是多少
解决方法就是记录下一个更大元素的数就可以了
class Solution {
public int[] dailyTemperatures(int[] temperatures) {
int n=temperatures.length;
Stack<Integer> elements=new Stack<>();
//同时存储索引
Stack<Integer> locations=new Stack<>();
//存放最后下一个更大的数的索引
int[] location=new int[n];
for(int i=n-1;i>=0;i--){
while(!elements.isEmpty()&&elements.peek()<=temperatures[i]){
elements.pop();
locations.pop();
}
location[i]=elements.isEmpty()?-1:locations.peek();
elements.push(temperatures[i]);
locations.push(i);
}
int[] res=new int[n];
for(int j=0;j<n;j++){
int num=location[j]-j;
if(num<=0){
res[j]=0;
}else{
res[j]=num;
}
}
return res;
}
}
或者是
int[] dailyTemperatures(int[] temperatures) {
int n = temperatures.length;
int[] res = new int[n];
// 这里放元素索引,而不是元素
Stack<Integer> s = new Stack<>();
/* 单调栈模板 */
for (int i = n - 1; i >= 0; i--) {
while (!s.isEmpty() && temperatures[s.peek()] <= temperatures[i]) {
s.pop();
}
// 得到索引间距
res[i] = s.isEmpty() ? 0 : (s.peek() - i);
// 将索引入栈,而不是元素
s.push(i);
}
return res;
}
3.503. 下一个更大元素 II
同样是求下一个更大元素,但是现在这个数组是环形的
比如输入
[2,1,2,4,3],你应该返回[4,2,4,-1,4],因为拥有了环形属性,最后一个元素 3 绕了一圈后找到了比自己大的元素 4。我们一般是通过 % 运算符求模(余数),来模拟环形特效:
int[] arr = {1,2,3,4,5}; int n = arr.length, index = 0; while (true) { // 在环形数组中转圈 print(arr[index % n]); index++; }
我们要如何处理呢?
难点在于最后一个元素如何找到比自己大的数
对于这种需求,常用的套路就是将数组长度翻倍
这样最后一个元素就能找到下一个更大的数,其他的数也能被正确计算
当然我们可以不构造新的数组而是利用循环数组的技巧来模拟数组长度翻倍的效果
完整的代码如下:
class Solution {
public int[] nextGreaterElements(int[] nums) {
Stack<Integer> elements=new Stack<>();
int n=nums.length;
int[] res=new int[n];
for(int i=2*n-1;i>=0;i--){
while(!elements.isEmpty()&&elements.peek()<=nums[i%n]){
elements.pop();
}
res[i%n]=elements.isEmpty()?-1:elements.peek();
elements.push(nums[i%n]);
}
return res;
}
}
这样就能很巧妙地解决环形数组的问题,时间复杂度是O(N)
总结
在这里说的单调栈的模板都是计算每个元素的下一个更大元素,但如果题目让你计算上一个更大的元素或者计算上一个更大或相等的元素又要如何修改对应的模板呢?
而且在实际的应用中,题目不会直接让你计算下一个或上一个更大或更小的元素,那又如何把问题转换成单调栈相关的问题呢?