【机器学习】集成学习—Boosting—GBM（Gradient Boosting Machine）解析

1. 介绍

前面我们在 https://blog.csdn.net/qq_51392112/article/details/130507112 了解了集成学习的相关知识。这一节我们讲什么是GBM，也就是Gradient Boosting Machine（梯度提升机）。

GBM 是一种集成算法（Boosting类）。常见的集成学习算法包括 Boosting，Bagging（也叫 Bootstrap Aggregating），Stacking 等。

• 其中 Boosting 包含经典的 AdaBoost 和 依靠梯度提升的 GBM。
  • GBDT 就属于 GBM 这类，它是基学习器为树模型的 GBM。
• 同类算法还有在 GBM 之上进行了全面优化的 XGBoost，以及进行了速度优化的 LightGBM 等。
• 如果用一张图来表示它们之间的关系，就是这样：
  
• GBDT 是 GBM 的一个特例，它的效果非常好，所以一提 GBM，最先会想到 GBDT。
  • GBDT 以 CART 为基学习器（此处也叫弱学习器），通过抑制基学习器的复杂度，缓解基学习器的过拟合风险，提高泛化能力。
  • 同时 GBDT 对多个基学习器串行训练，通过结果相加来对基学习器集成，提高拟合能力。

2. Boosting

2.1 1. 强 / 弱学习器

提升方法（Boosting）的主要思想是：把多个高偏差的弱学习器组合利用起来，降低整体偏差，形成一个强学习器。

• 弱学习器就是比随机分类稍好一点，比如随机分类正确率为 50%，错误率为 50%，那么弱学习器正确率就是刚刚超过 50% 一点，比如 55%，

• 而强学习器则是正确率很高很高，比如 90%，如下图：
  

• 为什么 Boosting 要用弱学习器呢？

  • 因为弱学习器容易得到，难度低，成本低。而且20 世纪的时候，还没有深度学习，弱学习器很多，强学习器较少
  • 学者幻想一种能够让“三个臭皮匠顶个诸葛亮”的算法，

• 因此， Boosting 这种思想就出来了。

2.1.2 AdaBoost

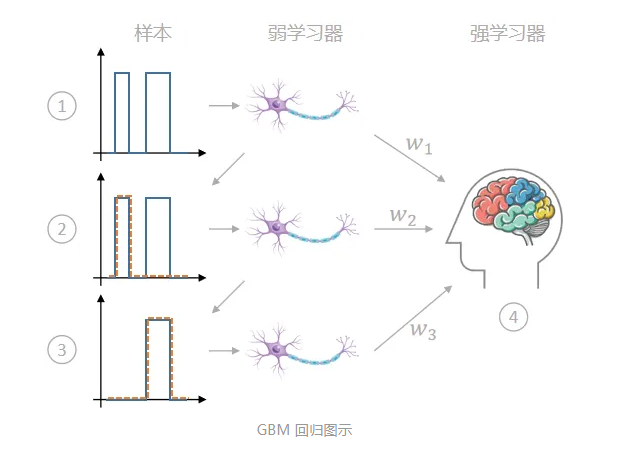
Boosting 的思想是：n 个弱学习器 -> 强学习器。它没有限定算法特点，能把弱变强即可，但大多数 Boosting 算法都会螺旋迭代式地训练弱学习器（串行，实现的时候可以并行），然后将结果加起来作为最终结果。形象点来说就是这样：

典型的boosting方法就是 AdaBoost（Adaptive Boosting），很多教材或博客讲 Boosting 的时候都会以 AdaBoost 为例。

• 这是因为 AdaBoost 是第一个实现了 Boosting 效果的算法。
• 上图所说的其实就是 AdaBoost 用于分类任务时的基本思想：
  • 先用弱学习器对样本分类；
  • 错分的样本在下一轮学习中提高权重；
  • 这样重复多次，得到多个弱学习器，并且每个弱学习器都学到一个权重 ；
  • 将多个弱学习器加权求和，得到想要的强学习器。

3. GBM

梯度提升机（Gradient Boosting Machine，GBM）是 Boosting 的另一种实现方式。

• 前面提到的 AdaBoost 是依靠调整预测错误数据样本的权重来训练新的学习器，进而降低偏差；

• 而 GBM 则是让新分类器拟合负梯度来降低偏差。
  

• 梯度提升机这个名字可能有一点迷惑性。

  • 我们都听过梯度下降算法，所以当听到梯度提升，可能会误以为这是让梯度提升的算法。
  • 然而并不是这样，提升 （Boosting）指的是让弱学习器变成强学习器，跟梯度没有半点关系。

• 所以梯度提升机应该这样理解：使用了梯度下降的提升机。

3.1 GBM 特例

为了便于理解，从特例讲起，然后再泛化到一般情况。

• GBM 最好理解的特例是无缩减（shrinkage）、损失函数取平方误差的回归情况。
• 假设我们想拟合一段正弦曲线，为此采了一系列的点，构成一个数据集：
  
  
  
  
  

3.2 梯度下降 - 参数空间

• 首先回顾下梯度下降。我们通常都是对模型参数进行梯度下降优化，比如神经网络。这个叫做参数空间的梯度下降。
  • 具体步骤是：
    • 1）首先用损失函数对各个参数求导，得到负梯度；
    • 2）然后用原始参数加上负梯度，实现一次迭代优化。公式如下：
      
    • 算法从初始位置顺着负梯度方向，走到局部最优点。
      

3.3 梯度下降 - 函数空间

与参数空间的梯度下降（针对 $\theta$ ）类似，GBM 是在函数空间（也就是针对 F(x) 这个函数）进行梯度下降。

• 先定义下对于 单个样本的平方误差 损失函数：
  
  我们的目标是降低整个训练集的损失值，它的计算公式是：
  
  
  这样，我们就得到了残差和负梯度的关系（损失取平方误差时）。
  

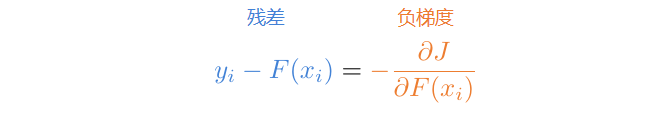
3.4 整体思路

• GBM 借鉴参数空间的梯度下降，得到了函数空间的梯度下降
• 当损失函数为平方误差时，负梯度恰好呈现残差形式
• 用一个新学习器去拟合残差，把新学习器结果加到原模型上，并反复加加加，慢慢逼近真实值。

再从公式角度小结下：

3.5 损失函数

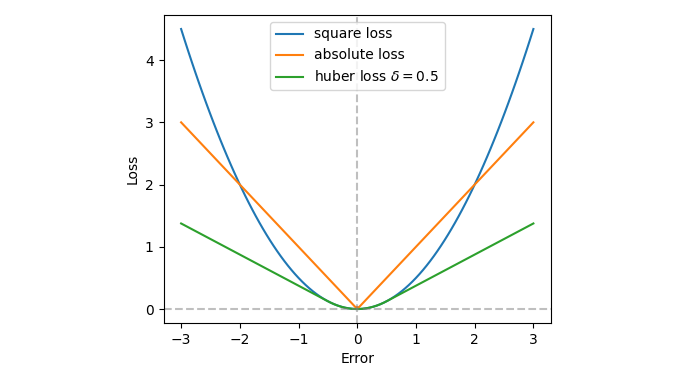
平方误差算起来很快，但是他有一个很大的问题：受不了异常点（下面会进行解释）。先说两个对异常点比较鲁棒的损失函数，分别是：

• 绝对值损失函数：
  
• Huber 损失函数：
  
• 三种损失函数可视化一下：（平方损失、绝对值损失、huber损失）
  
• 下面通过一张表格对比下他们对于异常情况的响应，最右边一列是异常样本。
  
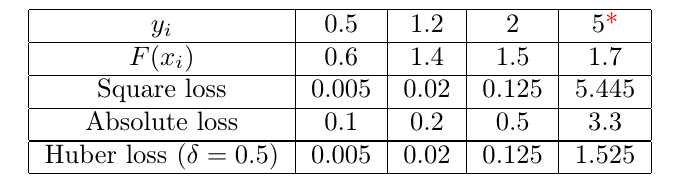
  分析：对于异常点 $y_i=5$，预测值正常为 1.7。
  • 这个时候平方损失为 5.445，最大，是 Huber 的 3.5倍；
  • 绝对值损失居中。绝对值误差在当前情况下，对于异常点的损失没有 Huber 小，说明鲁棒性没 Huber 好。
    那绝对值误差有什么优点呢？
    • 可以观察到，当误差小的时候，他的损失值相对更大，也就是说他对于拟合较好地样本也有很高地关注度。

3.6 缩减（shrinkage）

算法实现过程如伪代码所写：

• 1）先计算伪响应；
• 2）根据伪响应拟合新学习器，得到新学习器参数；
• 3）根据最速下降法的思想，求解最优步长；
• 4）更新集成模型，进入下一轮梯度下降过程。

4. GBDT

梯度提升决策树（Gradient Boosting Decision Tree，GBDT）是 GBM + CART。CART 作为 GBM 的基模型，GBM 做为 CART 的集成方法。虽然 GBM 可以跟任何回归器结合，但通常用的都是 GBM 与 CART 的组合，因为它的效果总体来说最好。在 sklearn 库里有现成的 GBDT 类，分别是：

• 分类器 GradientBoostingClassifier
• 回归器 GradientBoostingRegressor

两个类的名字里虽然没有 tree，但都默认是用 tree 作为基学习器，而且不能修改。GBM 和 GBDT 的公式差不多，但是 GBDT 有一个计算过程的优化，能快一些。

参考

【1】https://zhuanlan.zhihu.com/p/361036526
【2】Boosting - 维基百科 https://en.wikipedia.org/wiki/Boosting_(machine_learning)
【3】Greedy function approximation: a gradient boosting machine https://projecteuclid.org/journals/annals-of-statistics/volume-29/issue-5/Greedy-function-approximation-A-gradient-boosting-machine/10.1214/aos/1013203451.full
【4】A gentle introduction to gradient boosting https://www.ccs.neu.edu/home/vip/teach/MLcourse/4_boosting/slides/gradient_boosting.pdf
【5】《统计学习方法》李航