信号这个东西,我们是实际应用中用的大多都是模拟信号,比如说语音、地震、雷达、声纳信号,这些都是模拟信号,但是,计算机想要通过数学方法处理模拟信号,就要先将模拟信号转换成具有有限精度的数字序列,从模拟信号转换成数字信号,这一过程称为模数转换(A/D),反过来,数模转换就是(D/A),
A/D从概念上有三个步骤:
1、采样:
这个我知道,学计算机网络的时候接触了一点,奈奎斯特定理和香农定理,就是对连续信号在离散时间点处的样本值获取,设输入时,那么输出时
,同时,T是采样间隔。
2、量化:
离散时间连续信号转换到离散时间离散值(数字)信号的转换过程,每个信号样本值是从可能值的有限集中选取的。
量化误差:未量化样本和量化输出之间的差
3、编码:
欸一个离散值在编码过程汇总都会转换为b位长度的二进制序列。
二、模拟信号的采样:
方式有很多种,常用的方法是周期采样或者是均匀采样。
对模拟信号每隔T秒取样本值得到的离散时间信号:
:
在这一过程中,两个连续样本之间的时间间隔T被称为采样周期或者是采样间隔,其倒数F则被称为采样率(样本数/s)或者是采样频率(Hz)。
实际上,周期采样建立了连续时间信号的时间变量和离散时间信号的时间变量之间的关系,这些变量是通过采样周期T或者等价的通过采样率线性相关的,也就是:
那么,由上式就可以推出在模拟信号的频率变量F(或者)和离散时间信号的频率变量f(或者
)之间的一种关系,举个例子,假设这里有一个信号:
如果我们以个样本/s的采样率进行周期采样,那么,上面的这个信号就变成了:
再和这个信号作比较:
,
这里我们可以注意到,F和f是由线性关系的:
也就是说:
这样子,我们就知道了:只要我们知道了采样率,就可以用f来确定以赫兹为单位的频率F。
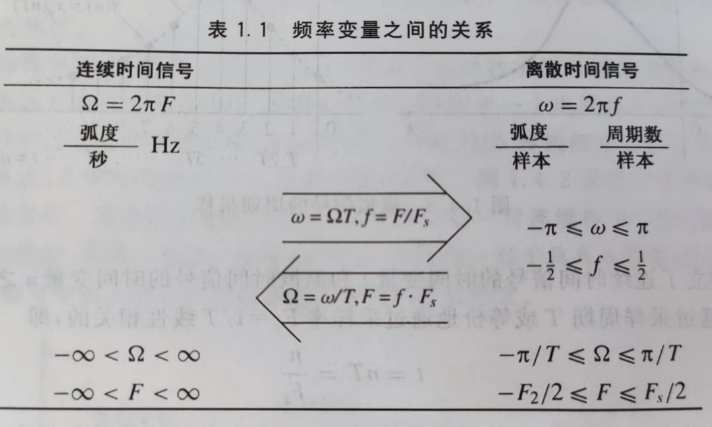
世家上,连续时间信号和离散时间信号的基本不同就在于频率F和f(或者和
)的取值范围不同,书上有张频率变量之间的关系表格,我给贴上来:
其实我一直很不解,sin是正弦啊,为什么书上说cos是正弦信号呢?
然后我问了问学通信的同学,得到了一个不算解释的解释:信号与系统和通原里面,cos和sin都被称做正弦信号,原因就是,从诱导公式出发,正弦和余弦就差了个相位,在处理的时候,就把他俩统称正弦信号了。。。。。。。。。。当事人在风中凌乱。。。。。。。。。。。。。。。
一般来说,连续时间正弦信号:以
的采样率采样,将会产生一个离散时间信号:
,其中,
是正弦信号的相对频率。
无数的连续时间正弦信号通过采样可以由相同的离散时间信号(相同样本集)表示。
看的人麻,不知所云的情况下,我觉得,还不如直接看采样定理,这个起码是个定理,还好懂一些,
采样定理的目的就是,对于一个给定的模拟信号,通过采样定理来选择采样周期T或者采样率。
如果我们直到一般类型信号的最大频率范围,那么就可以指定将模拟信号转换成数字信号所必须的采样率。
假设哈,任何模拟信号都可以表示成不同振幅、频率和相位的正弦信号的和:
其中N代表的是频率成分的数目,所有信号都可以通过任意的短时分割服从于注意表示形式,这些振幅、频率和相位通常会从一个时间段到另一个时间段随着时间慢慢改变,但是,要假定,这些信号的频率不i会超过某个已知频率Fmax,这个Fmax就是我们需要的,有了Fmax,我们就能选择合适的信号。
采样定理:如果包含在某个模拟信号中的最高频率是Fmax=B,而信号以采样率
,那么
可以从样本值中准确恢复出来, 插值函数是:
所以,也就可以表示为:
其中,就是
的样本。
当的采样以最小采样率
执行的时候,上面的公式就变成了:
,
采样率称为奈奎斯特率。
我记得之前,计网里面有两个定理,一个是奈奎斯特,一个是香农,忘光了忘光了,在网上找了一下,在这给大家写一下,也当时大家都在复习了:
奈奎斯特:
如果一个系统以超过信号最高频率至少两倍的速率对模拟信号进行均匀采样,那么原始模拟信号就能从采样产生的离散值中完全恢复。
为了防止由于混叠引起的信号被破坏,需要以奈奎斯特速率或更高的速率进行采样。如果不遵守这个基本要求,就无法消除混叠(混叠永久与原始频谱混合,两者无法区分)。
香农:
给出了信道信息传送速率的上限(比特每秒)和信道信噪比及带宽的关系。香农定理可以解释现代各种无线制式由于带宽不同,所支持的单载波最大吞吐量的不同。
在有随机热噪声的信道上传输数据信号时,信道容量Rmax与信道带宽W,信噪比S/N关系为: Rmax=W*log2(1+S/N)。注意这里的log2是以2为底的对数。
emm,我觉得,到现在,啥都不会,成废物了。。。。。。。