莱昂哈德·欧拉(Leonhard Euler)的一生,是为数学发展而奋斗的一生,他不但为数学界作出贡献,更把整个数学推至物理的领域。欧拉杰出的智慧,顽强的毅力,孜孜不倦的奋斗精神和高尚的科学道德,永远值得我们学习。
01 著作等身

-童年尽显才学天赋
欧拉小时候他就特别喜欢数学,不满10岁就开始自学《代数学》。这本书连他的几位老师都没读过,可小欧拉却读得津津有味,遇到不懂的地方,就用笔作个记号,事后再向别人请教。1720年,年仅13岁的欧拉靠自己的努力考入了巴塞尔大学,成为了这所大学乃至整个瑞士大学校园里年龄最小的学生。同时,欧拉还得到当时最有名的数学家约翰·伯努利(Johann Bernoulli,1667-1748年)的精心指导。这在当时被看做是个奇迹,曾轰动了数学界。
-毕生著作浩瀚如烟
欧拉从19岁开始发表论文,直到76岁,半个多世纪的时间里他总共写下了886本书籍和论文,其中分析、代数、数论占40%,几何占18%,物理和力学占28%,天文学占11%,弹道学、航海学、建筑学等占3%,彼得堡科学院为了整理他的著作,足足忙碌了四十七年。
-数学领域贡献颇多
如今,几乎每一个数学领域都可以看到欧拉的名字,从初等几何的欧拉线,多面体的欧拉定理,立体解析几何的欧拉变换公式,到数论中的欧拉函数,微分方程的欧拉方程,级数论的欧拉常数,复变函数的欧拉公式等等,数也数不清。欧拉对数学分析的贡献更独具匠心,《无穷小分析引论》一书便是他划时代的代表作,当时数学家们称他为"分析学的化身"。
除著作之外,欧拉还创设了许多数学符号,例如π(1736年),i(1777年),e(1748年),sin和cos(1748年),tg(1753年),△x(1755年),Σ(1755年),f(x)(1734年)等。
欧拉发明的欧拉公式曾被称为“上帝公式”,里面最著名的有拓扑学的多面体公式,幅角公式,以及初等的数论中的函数的公式。我们所学的级数、概率、函数等很多都是根据欧拉发明的这个公式所衍生出来的。

02 身残志坚

-独眼巨人丈量世界
在欧拉的数学生涯中,他的视力一直在恶化。在1735年一次几乎致命的发热后的三年,他的右眼近乎失明,但他把这归咎于他为圣彼得堡科学院进行的辛苦的地图学工作。视力在他在德国期间也持续恶化,以至于弗雷德里克把他誉为“独眼巨人”。欧拉的原本正常的左眼后来又遭受了白内障的困扰。在他于1766年被查出有白内障的几个星期后,导致了他的近乎完全失明。
沉重的打击并没有使欧拉倒下,他以惊人的毅力,凭着记忆和心算进行研究,直到逝世。欧拉可以从头到尾不犹豫地背诵维吉尔的史诗《埃涅阿斯纪》,并能指出他所背诵的那个版本的每一页的第一行和最后一行是什么。当大火烧掉他几乎全部的著述之后,欧拉用了一年的时间口述了所有这些论文并作了修订。欧拉失明后的17年间,他还口述了几本书和400篇左右的论文。在书记员的帮助下,欧拉在多个领域的研究反而变得比之前更加高产了。在1775年,他平均每周就完成一篇数学论文。
03 跨界大师

-数学音乐跨界“联名”
1739年,欧拉写下了《音乐新理论的尝试》(Tentamen novae theoriae musicae),书中试图把数学和音乐结合起来。一位传记作家写道:这是一部"为精通数学的音乐家和精通音乐的数学家而写的"著作。
-数独前身趣味游戏
18世纪的欧洲,数学家莱昂哈德·欧拉总结了当时流行的一种填字游戏,称为“拉丁方阵”(Latin square)。游戏的规则即是在n阶的方形网格中填入n种拉丁字母(类似于2阶数独中,填入数字1~2,而3阶数独中填入1~3),使得每行、每列的字母都不会重复。这种方阵不限于9阶,也没有宫的限制,但保留了数独最基本的“每行每列不重复”的要求。
不过让欧拉着迷的是拉丁方阵的一种更复杂的版本。欧拉考虑往每个格子中填入一个拉丁字母和一个希腊字母,使得每行、每列的字母都不会重复,并且每个格子中的希腊-拉丁字母对也不重复。这种方阵叫做“希腊-拉丁方阵”(Graeco-Latin square),其实质是将两个正交拉丁方阵(orthogonal Latin squares)并成一个方阵,这里的“正交”是指两个方阵对应格子组成的有序对不重复。这便是后来20世纪开始风靡全球的数独游戏的前身。
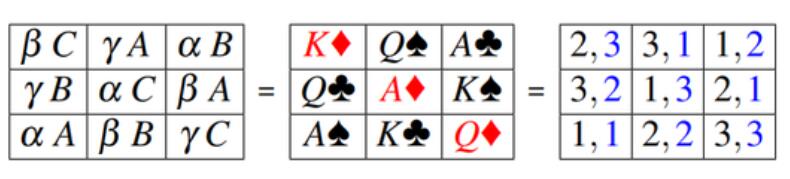
法国数学家皮埃尔-西蒙·拉普拉斯曾这样评价欧拉对于数学的贡献:“读欧拉的著作吧,在任何意义上,他都是我们的大师。”
欧拉能在学术领域获得如此之高的成就,除了与他天资过人有关外,也和他顽强的毅力以及要把毕生都奉献于学术研究的科研精神有关。希望大家在了解欧拉的逸闻趣事之余,也要学习他坚持不懈的钻研精神,在自己的学术领域里发光发热!
资料来源
http://fjscdsxxh.com/news/show-55-145.html
https://factsking.com/historical-people/leonhard-euler-facts/
https://www.thoughtco.com/leonhard-euler-biography-4174374





![[东华杯2021] ezgadget](https://img-blog.csdnimg.cn/959da7f0ebb04b76ac997453a5d86579.png)