文章目录
- 一.什么是栈
- 二. 栈的使用
- 2.1栈的基本操作
- 2.2 栈的基本使用
- 三.栈的实现
- 3.1 数组实现栈的方式
- 3.2 链式栈的实现
- 四.栈的应用
- 4.1 括号匹配
- 4.2 逆波兰表达式求值
- 什么是逆波兰表达式
- 4.3 出栈入栈次序匹配
- 4.4 最小栈
- 五.总结
一.什么是栈
- 栈是一种先入后出(FILO)的线性表数据结构
- 添加和删除操作只在表的一端进行,这一端称为栈顶,另一端称为栈底
- 添加操作又称入栈或进栈,删除操作又称出栈
例如手枪的弹夹就是诸如此类的结构

二. 栈的使用
2.1栈的基本操作
栈有插入操作和删除操作,这俩个操作本身就叫入栈和出栈.具体如下图所示.
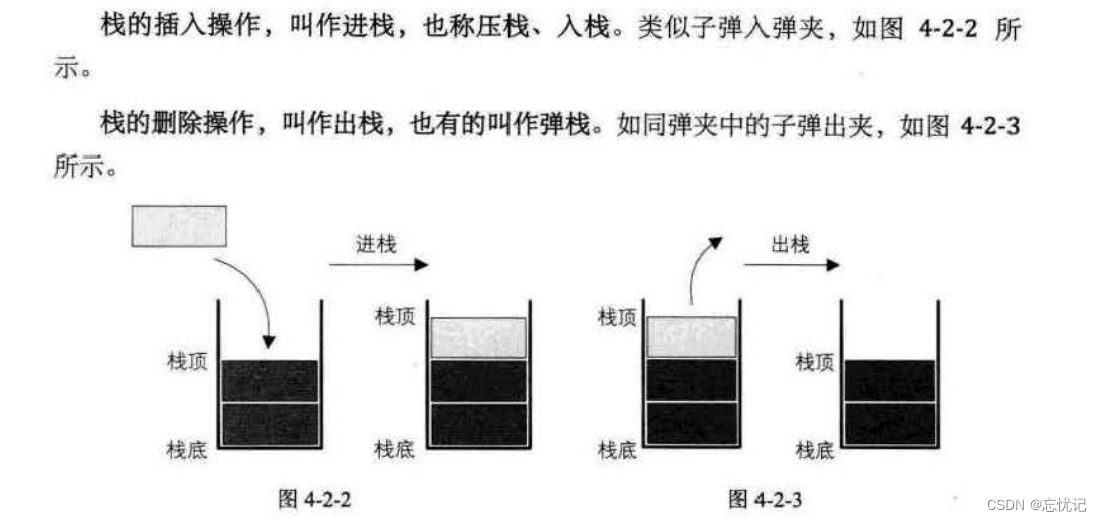
2.2 栈的基本使用
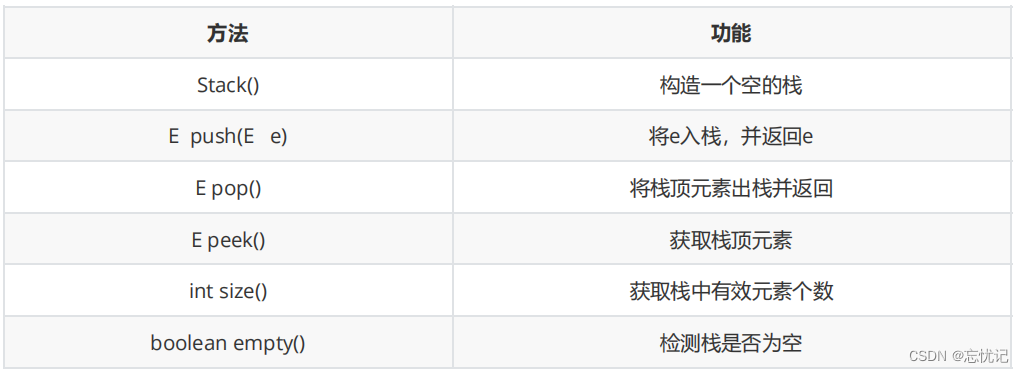
public static void main(String[] args) {
Stack<Integer> s = new Stack();
s.push(1);
s.push(2);
s.push(3);
s.push(4);
System.out.println(s.size()); // 获取栈中有效元素个数---> 4
System.out.println(s.peek()); // 获取栈顶元素---> 4
s.pop(); // 4出栈,栈中剩余1 2 3,栈顶元素为3
System.out.println(s.pop()); // 3出栈,栈中剩余1 2 栈顶元素为3
if(s.empty()){
System.out.println("栈空");
}else{
System.out.println(s.size());
}
}
三.栈的实现
- 可以使用数组或链表实现栈
- 使用数组实现时,数组的一端作为栈顶,另一端作为栈底
- 使用链表实现时,链表的头节点作为栈顶,尾节点作为栈底
- 实现需要包含的方法有:入栈push、出栈pop、获取栈顶top、判断是否为空isEmpty等
3.1 数组实现栈的方式
public class MyStack {
public int[] elem;
public int usedSize;
public MyStack() {
this.elem = new int[10];
}
//压栈
public void push(int val) {
if(isFull()) {
//扩容
elem = Arrays.copyOf(elem,2*elem.length);
}
elem[usedSize++] = val;
}
public boolean isFull() {
return usedSize == elem.length;
}
//出栈
public int pop() {
if(isEmpty()) {
throw new EmptyException("栈是空的!");
}
/*int val = elem[usedSize-1];
usedSize--;
return val;*/
/* usedSize--;
return elem[usedSize];*/
return elem[--usedSize];
}
public boolean isEmpty() {
return usedSize == 0;
}
public int peek() {
if(isEmpty()) {
throw new EmptyException("栈是空的!");
}
return elem[usedSize-1];
}
}
这段代码实现了一个数组栈,有以下几点:
- 使用数组elem存储栈元素,usedSize表示栈的大小。
- 构造方法初始化elem数组长度为10。
- 入栈操作先判断栈是否为满,若满则扩容为原来的2倍。然后将新元素添加至数组末端,usedSize增加1。
- isFull方法判断栈是否为满,usedSize是否等于elem数组长度。
- 出栈操作先判断栈是否为空,若为空则抛出异常。然后usedSize减1,返回出栈元素。
- isEmpty方法判断usedSize是否为0,来判断栈是否为空。
- peek方法获取栈顶元素,判断非空后返回elem[usedSize-1]。
- 扩容使用Arrays.copyOf()方法实现,扩容为原来的2倍。
时间复杂度:
- push:O(n),取决于是否扩容。未扩容为O(1),扩容为O(n)。
- pop和peek:O(1)。
- isEmpty和isFull:O(1)。
空间复杂度:O(n),数组elem的大小。
3.2 链式栈的实现
private class Node {
int val;
Node next;
public Node(int val) {
this.val = val;
}
}
private Node top; // 栈顶指针
// 入栈
public void push(int val) {
Node node = new Node(val);
if (top == null) {
top = node;
return;
}
node.next = top;
top = node;
}
// 出栈
public int pop() {
if (top == null) {
throw new RuntimeException("栈空");
}
int val = top.val;
top = top.next;
return val;
}
// 获取栈顶元素
public int top() {
if (top == null) {
throw new RuntimeException("栈空");
}
return top.val;
}
// 判断栈是否为空
public boolean isEmpty() {
return top == null;
}
这个实现使用链表来构建栈。有以下几点:
- 私有内部类Node用于表示栈节点,包含val和next两个属性。
- top指针指向栈顶,初始指向null。
- 入栈操作将新节点的next指向栈顶,然后将top指向新节点。
- 出栈操作将top指向栈顶的next,并返回该出栈节点的值。
- 获取栈顶与判断非空操作均依赖top是否指向null。
- 额外判断栈空的情况,避免空指针异常。
时间复杂度:入栈和出栈为O(1),与栈的大小无关。其他操作也均为O(1)。
空间复杂度:O(n),取决于栈中元素的个数。
四.栈的应用
4.1 括号匹配
题目链接
具体思路:
- 定义一个栈,用于存储左括号。
- 遍历输入字符串的每个字符。
- 如果遇到左括号(、[或{,则将其压入栈。
- 如果遇到右括号),则弹出栈顶元素,并判断是否匹配。如果匹配则继续遍历,如果不匹配则返回false。
- 如果遇到右括号]或},同理弹出栈顶元素判断是否匹配,不匹配则返回false。
- 遍历结束后,如果栈为空则返回true,否则返回false

代码如下:
public boolean isValid(String s) {
Stack<Character> stack = new Stack<>();
for (int i = 0; i < s.length(); i++) {
char ch = s.charAt(i);
if(ch == '(' || ch == '{' || ch == '[') {
stack.push(ch);
}else {
//遇到了右括号
if(stack.empty()) {
return false;
}
char ch2 = stack.peek();//左括号
if(ch == ')' && ch2 == '(' || ch == '}' && ch2 == '{' || ch == ']' && ch2 == '[') {
stack.pop();
}else {
return false;//不匹配
}
}
}
if(!stack.empty()) {
return false;
}
return true;
}
4.2 逆波兰表达式求值
题目链接
什么是逆波兰表达式
我这里做出简单的一个解释,简单来说就是后缀表达式,我这里做出一个简单的图示
 具体思路:
具体思路:
- 定义一个栈,用于存储操作数。
- 遍历字符串数组tokens中的每个元素。
- 如果当前元素不是运算符,则直接将其PARSE为整数并压入栈。
- 如果当前元素是运算符,则弹出栈顶的两个操作数进行运算。
- 根据运算符不同,进行加减乘除运算。将结果压入栈。
- 遍历结束后,栈顶元素为最终结果,弹出并返回。

代码如下:
public int evalRPN(String[] tokens) {
Stack<Integer> stack = new Stack<>();
for(String x : tokens){
if(!isOperation(x)) {
stack.push(Integer.parseInt(x));
}else {
int num2 = stack.pop();
int num1 = stack.pop();
switch (x) {
case "+":
stack.push(num1+num2);
break;
case "-":
stack.push(num1-num2);
break;
case "*":
stack.push(num1*num2);
break;
case "/":
stack.push(num1/num2);
break;
}
}
}
return stack.pop();
}
private boolean isOperation(String x) {
if(x.equals("+") || x.equals("-") || x.equals("/")||x.equals("*")) {
return true;
}
return false;
}
4.3 出栈入栈次序匹配
题目链接
具体思路:
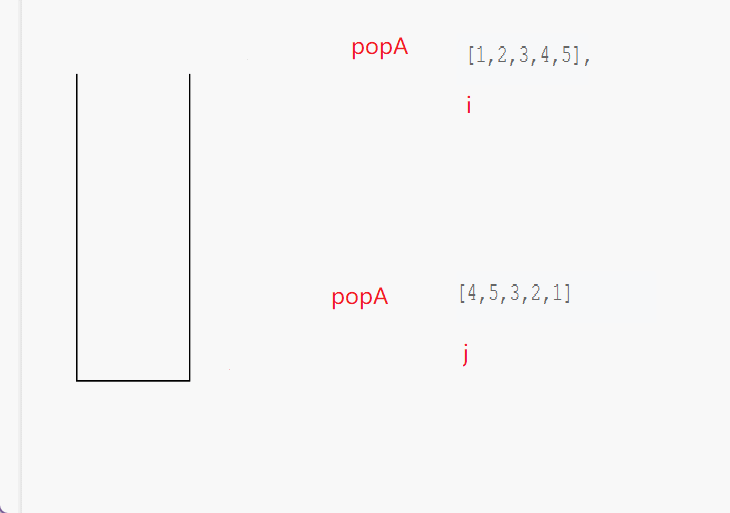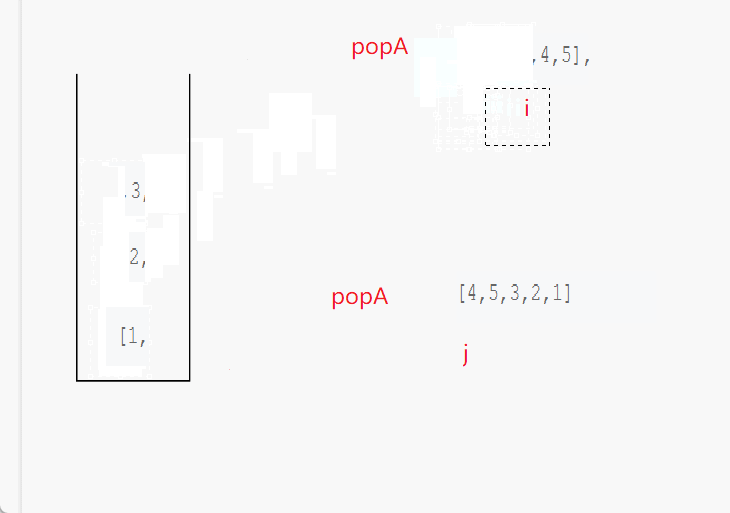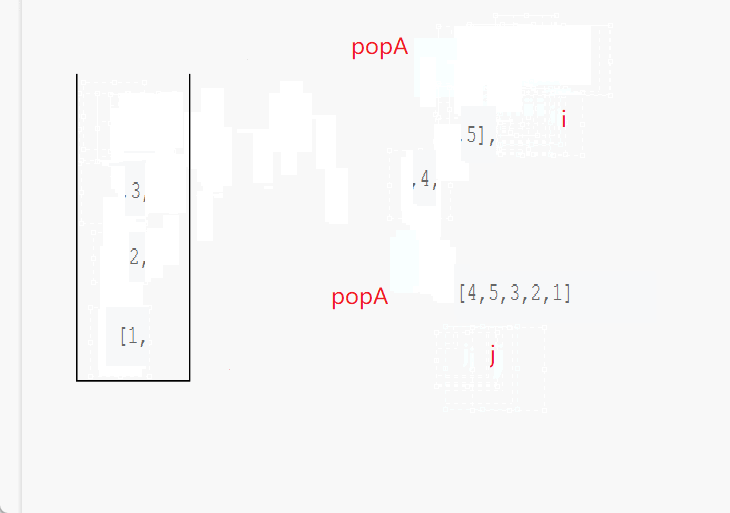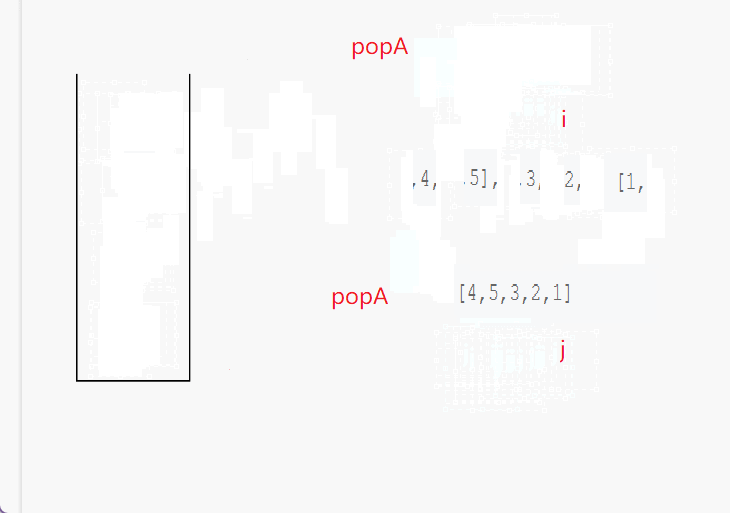
- 定义一个栈stack和两个索引i和j,i用于遍历pushA,j用于遍历popA。
- 循环遍历pushA,每次将当前元素pushA[i]入栈。
- 当栈不为空 && 栈顶元素等于popA[j]时,循环弹出栈顶元素。同时j++。
- 遍历pushA结束后,检查栈是否为空。如果为空则popA为pushA的弹出序列,返回true;否则返回false
代码如下:
public boolean isPopOrder(int [] pushA,int [] popA) {
Stack<Integer> stack = new Stack<>();
int j = 0;
for (int i = 0; i < pushA.length; i++) {
stack.push(pushA[i]);
while (j < popA.length && !stack.empty() && stack.peek().equals(popA[j])) {
stack.pop();
j++;
}
}
return stack.empty();
}
4.4 最小栈
题目链接
具体思路:
- 使用两个栈,stack用于存储所有元素,minStack用于存储当前最小元素。
- 在push操作中,先将元素val入栈stack,然后判断minStack是否为空或val是否小于等于minStack的栈顶元素。
- 如果minStack为空或val小于等于minStack栈顶,则也将val入栈minStack。这样minStack的栈顶始终是当前最小值。
- 在pop操作中,先从stack弹出元素,然后判断此元素是否等于minStack的栈顶元素,如果相等则也从minStack弹出,以保持minStack的栈顶为当前最小值。
- 在getMin操作中,直接返回minStack的栈顶元素,为当前最小值。
代码如下:
import java.util.Stack;
class MinStack {
private Stack<Integer> stack ;
private Stack<Integer> minStack ;
public MinStack() {
stack = new Stack<>();
minStack = new Stack<>();
}
public void push(int val) {
stack.push(val);
if(minStack.empty()) {
minStack.push(val);
}else {
if(val <= minStack.peek()) {
minStack.push(val);
}
}
}
public void pop() {
if(!stack.empty()) {
Integer val = stack.pop();
//维护最小栈
if (val.equals(minStack.peek())) {
minStack.pop();
}
}
}
// peek
public int top() {
if(!stack.empty()) {
return stack.peek();
}
return -1;
}
public int getMin() {
return minStack.peek();
}
}
五.总结
- 栈是一种先入后出的线性表数据结构
- 可以使用数组或链表实现栈,实现需要包含的方法有入栈push、出栈pop等
- 栈操作的时间复杂度均为O(1)
- 栈有许多重要应用,如递归调用、表达式求值、浏览器的前进后退等




![[pgrx开发postgresql数据库扩展]附1.存储过程的优缺点与数据库扩展函数](https://img-blog.csdnimg.cn/img_convert/cdbbe4b5116cdb91bdea33d185958cb2.webp?x-oss-process=image/format,png)