DP(9)--插头DP
/*
Mondriaan’s Dream题目大意:在 N*M 的棋盘内铺满 1*2 或 2*1 的多米诺骨牌,求方案数。
砖只有横放和竖放两种状态,把横放记为两个0,竖放记为上1下0,逐格DP,每次无论前一格放怎么放,
当前格可竖放或不放,而如果前一格是1,且当前格是0,那么我们可以把前一格改成0,再把当前格也放上0组成一块。
这样成对合并和生成插头。
*/
#include <iostream>
#include <string.h>
using namespace std;
const int W = 11;
long long f[2][1 << W];
// 将a的第b位取反,最低位编号为0
int flapBit(int a, int b)
{
return a ^ (1 << b);
}
// O(h*w*2^w), 交换为了得到窄列,降低时间复杂度
long long calc(int h, int w)
{
if (h < w)
swap(h, w);
memset(f, 0, sizeof(f));
int cur = 0;
f[cur][0] = 1;
for (int i = 0; i < h; ++i)
for (int j = 0; j < w; ++j)
{
cur ^= 1;
memset(f[cur], 0, sizeof(f[cur]));
for (int k = 0; k < (1 << w); ++k) // 枚举状态
{
if (f[cur^1][k] > 0)
{
f[cur][flapBit(k, j)] += f[cur^1][k]; // 竖放或不放
if (j != w - 1 && (!((k >> j) & 3))) // 非最后一列且满足能容纳2个单位的宽度
f[cur][flapBit(k, j+1)] += f[cur^1][k]; // 横放
}
}
}
return f[cur][0];
}
int main()
{
int h, w;
while (cin >> h >> w && h != 0 && w != 0)
cout << calc(h, w) << endl;
return 0;
}
一个方向的插头存在表示这个格子在这个方向可以与外面相连。
对于一个4连通的问题来说,它通常有上下左右4个插头。

插头的连通性(有没有下插头,与轮廓线直接相连的插头)
砖只有横放和竖放两种状态,把横放记为两个0,竖放记为上1下0,逐格DP,每次无论前一格放怎么放,当前格可竖放或不放,
而如果前一格是1,且当前格是0,那么我们可以把前一格改成0,再把当前格也放上0组成一块。
dp[i][j][state] 为位置(i,j),状态为state的方案数
插头存在信息 格子连通信息

优化为位置(i,j)插头的连通状态为S的方案数: f(i, j, S)
f(3, 1, {1, 0, 1, 2, 2}), f(3, 2, {1, 0, 1, 2, 2}), f(3, 3, {1, 0, 0, 0, 1})




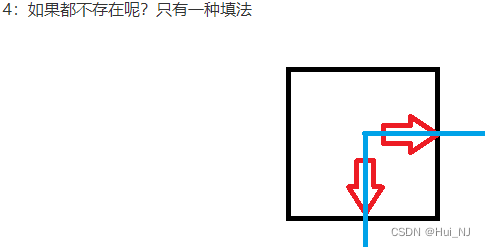
情况1 新建一个连通分量,这种情况出现在(i, j)有右插头和下插头。
新建的两个插头连通且不与其他插头连通,这种情况下需要将这两个插头
连通分量标号标记为一个未标记的正数,重新O(n)扫描保证新的状态满足最小表示。
情况2 合并两个连通分量,这种情况出现在(i, j)有上插头和左插头。
如果两个插头不连通,那么将两个插头所处的连通分量合并,标记相同的连通块标号,
O(n)扫描保证最小表示;如果已经连通,相当于出现一个回路,这种情况只能出现在最后一个非障碍格子。
情况3 保持原来的连通分量,这种情况出现在(i, j)的上插头和右插头恰好有一个或下插头和左插头也恰好有一个。
下插头或右插头相当于上插头或左插头的延续,连通块标号相同,并且不会影响到其他的插头的连通块标号,
计算新的状态的时间为O(1).
注意当从一行的最后一个格子转移到下一行的第一个格子的时候,轮廓线需要特殊处理。
值得一提的是,上面三种情况计算新的状态的时间分别为O(n), O(n), O(1), 如果使用前面提到的第二种最小表示法,
情况1只需要O(1),但是情况3可能需要O(n)重新扫描。
对n+1个元素进行编码,将其表示成一个n+1位的p进制数,p可以取能够达到的最大的连通块标号加1,
对本题来说,最多出现n/2<=6个连通块,不妨取p=7,在不超过数据类型范围的前提下,建议将p改为2的幂,
因为位运算比较快,本题最好采用8进制来存储。
如需大范围修改连通块标号,最好将状态O(n)解码到一个数组中,修改后再O(n)计算出新的p进制数,
而对于只需要局部修改几个标号的情况下,可以直接用(x/p^(i-1))%p来获取第i位,用加或者减k*p^(i-1)
直接对第i位进行修改。
唯一特殊的是上一行末到这一行头的处理。上一行末不可能有右插头,那我们直接把上一行末状态的表示最后是否存在右插头的位置去掉,
再添加一个表示没有左插头的位,就表示出了下一行行首的状态,为了方便写,在代码里,用dp[i][0][mask]表示转移后的上一行行末状态。
//https://www.luogu.com.cn/problem/P5056
#include <iostream>
#include <string.h>
using namespace std;
const int M = 15;
const int offset = 3, mask = (1 << offset) - 1;
int n, m;
long long ans;
//MaxSZ: 合法状态的上界,可以估计,也可以预处理出较为精确的值。
//Prime: 一个小于 MaxSZ 的大素数
const int MaxSZ = 16796, Prime = 9973;
bool path[M][M];
struct hashTable
{
/*
head[] 表头节点的指针。
next[] 后续状态的指针。
state[] 节点的状态。
key[] 节点的关键字,在本题中是方案数。
*/
int head[Prime], next[MaxSZ], sz;
long long state[MaxSZ];
long long key[MaxSZ];
/* 初始化函数,和手写邻接表类似,我们只需要初始化表头节点的指针 */
inline void init()
{
sz = 0;
memset(head, -1, sizeof(head));
}
/*
状态转移函数,其中 d 表示每次状态s转移所带来的增量。
如果找到的话就 +=,否则就创建一个状态为 s,关键字为 d 的新节点
*/
inline void push(long long s, long long d)
{
int x = s % Prime;
for (int i = head[x]; ~i; i = next[i])
{
if (state[i] == s) // s状态存在,直接更新key[]
{
key[i] += d;
return;
}
}
// 添加新状态
state[sz] = s;
key[sz] = d;
next[sz] = head[x];
head[x] = sz++;
}
}H[2];
/*
code[]: 轮廓线上的插头的状态编码
arr[]: 最小表示法的编码过程中,每个数字被映射到的最小数字。0表示插头不存在,不能被映射到其他值。
*/
int code[M + 1], arr[M + 1];
/*
最小表示法 m<=12 最多只有6个不同的连通分量,
对m+1个元素进行编码,将其表示成一个m+1位的p进制数,p可以取能够达到的最大的连通块标号加1,
本题最好采用8进制来存储, 将插头连通状态数组code进行8进制压缩,转为8进制数s。
*/
long long encode()
{
long long s = 0;
memset(arr, -1, sizeof(arr));
// 最小表示法,连通块编号从1开始
int bn = 1;
arr[0] = 0;
for (int i = 0; i <= m; ++i)
{
if (!~arr[code[i]]) // arr[] 为 -1, 即出现一个新的连通分量,添加新编号
arr[code[i]] = bn++;
s <<= offset; // 逐位进行8进制压缩
s |= arr[code[i]];
}
return s;
}
// 将8进制压缩码解析到code数组
void decode(long long s)
{
for (int i = m; i >= 0; --i)
{
code[i] = s & mask;
s >>= offset;
}
}
void push(int cur, int j, int dn, int rt, long long d)
{
code[j-1] = dn;
code[j] = rt;
H[cur].push(encode(), d);
}
int main()
{
cin >> n >> m;
char str[32] = { '\0' };
int row = 0, colum = 0;
for (int i = 1; i <= n; ++i)
{
cin >> str+1;
for (int j = 0; j <= m; ++j)
if (str[j] == '.')
{
path[i][j] = true;
row = i;
colum = j;
}
else
path[i][j] = false;
}
if (!row)
{
cout << 0 << endl;
return 0;
}
int cur= 0;
H[cur].init();
long long d = 1; // 初始状态0的增量delta为1
H[cur].push(0, d);
for (int i = 1; i <= n; ++i)
{
for (int j = 1; j <= m; ++j)
{
if (path[i][j])
{
cur ^= 1;
H[cur].init();
for (int s = 0; s < H[cur^1].sz; ++s)
{
decode(H[cur^1].state[s]); // 取出状态,并解码
d = H[cur^1].key[s]; // 得到增量 delta
int lt = code[j-1], up = code[j]; // 左插头,上插头
if (lt && up) // 如果左、上均有插头
{
if (lt == up) // 来自同一个连通块
{
if (i == row && j == colum) // 只有在最后一个格子时,才能合并,封闭回路。
push(cur, j, 0, 0, d);
}
else // 否则,必须合并这两个连通块,因为本题中需要回路覆盖
{
for (int k = 0; k <= m; ++k)
if (code[k] == lt)
code[k] = up;
push(cur, j, 0, 0, d);
}
}
else if (lt || up) // 如果左、上之中有一个插头
{
int t = lt | up;// 得到这个插头
if (path[i+1][j]) // 如果可以向下延伸
push(cur, j, t, 0, d);
if (path[i][j+1]) // 如果可以向右延伸
push(cur, j, 0, t, d);
}
else // 如果左、上均没有插头
{
if (path[i+1][j] && path[i][j+1]) // 生成一对新插头
push(cur, j, 7, 7, d); // 插头连通分量最大值不超过7
}
}
}
}
/* 迭代完一整行之后,滚动轮廓线 */
for (int j =0; j < H[cur].sz; ++j)
H[cur].state[j] >>= offset;
}
cout << (H[cur].sz > 0 ? H[cur].key[0] : 0) << endl;
return 0;
}
/*
测试数据
4 4
**..
....
....
....
2
4 4
....
....
....
....
6
12 12
..**********
...*********
....********
*....*******
**....******
***....*****
****....****
*****....***
******....**
*******....*
********....
*********...
1
*/
参考:
https://oi-wiki.org/dp/plug/


![[pgrx开发postgresql数据库扩展]附1.存储过程的优缺点与数据库扩展函数](https://img-blog.csdnimg.cn/img_convert/cdbbe4b5116cdb91bdea33d185958cb2.webp?x-oss-process=image/format,png)