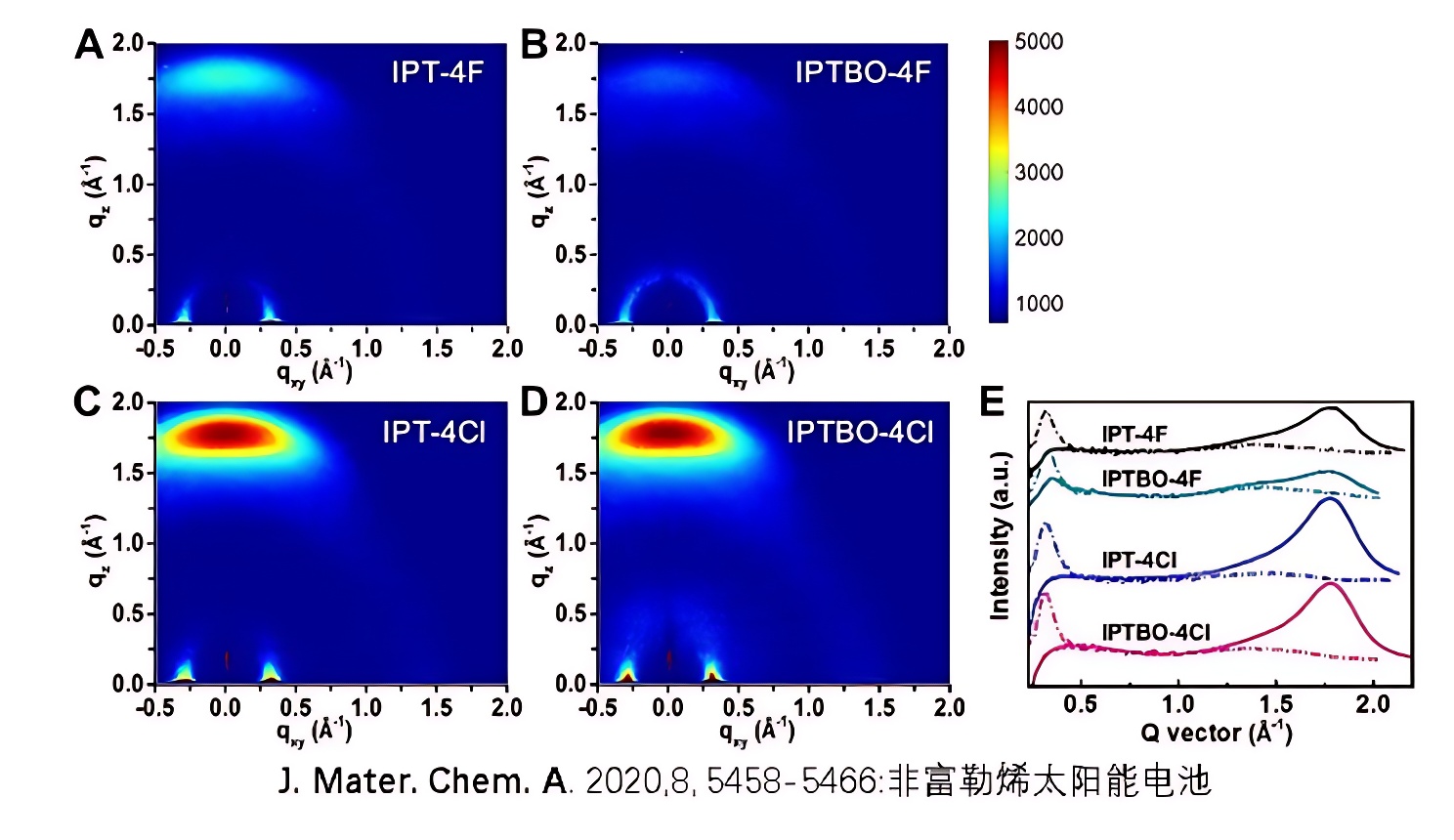
1. 什么是位置编码，为什么要使用位置编码

简单来说位置编码就是给一个句子中的每个token一个位置信息，通过位置编码可以明确token的前后顺序关系。

对任何语言来说，句子中词汇的顺序和位置都是非常重要的。它们定义了语法，从而定义了句子的实际语义。RNN结构本身就涵盖了单词的顺序，RNN按顺序逐字分析句子，这就直接在处理的时候整合了文本的顺序信息。

但Transformer架构抛弃了循环机制，仅采用多头自注意机制。避免了RNN较大的时间成本。并且从理论上讲，它可以捕捉句子中较长的依赖关系。

由于句子中的单词同时流经Transformer的编码器、解码器堆栈，模型本身对每个单词没有任何位置信息的。因此，仍然需要一种方法将单词的顺序整合到模型中。

想给模型一些位置信息，一个方案是在每个单词中添加一条关于其在句子中位置的信息。我们称之为“信息片段”，即位置编码。

2. 两种简单的位置编码

最容易想到两种位置编码：
（1）为每个时间步添加一个0-1范围内的数字，其中0表示第一个单词，1表示最后一个单词。

我喜欢吃洋葱 【0 0.16 0.32.....1】

我真的不喜欢吃洋葱【0 0.125 0.25.....1】

问题：我们可以看到，如果句子长度不同，那么位置编码是不一样，所以无法表示句子之间有什么相似性。

（2）1-n正整数范围分配

我喜欢吃洋葱 【1，2，3，4，5，6】

我真的不喜欢吃洋葱【1，2，3，4，5，6，7】

问题：往往句子越长，后面的值越大，数字越大说明这个位置占的权重也越大，这样的方式无法凸显每个位置的真实的权重。

3. Transformer的位置编码

可以看到上面两种简单的位置编码方式都有明显的不足，理想情况下，应满足以下标准：

• 每个时间步都有唯一的编码。
• 在不同长度的句子中，两个时间步之间的距离应该一致。
• 模型不受句子长短的影响，并且编码范围是有界的。（不会随着句子加长数字就无限增大）
• 必须是确定性的。

Transformer的作者设计了一种可以满足上面要求的三角函数位置编码方式。首先为每个不同位置的单词(token)单独生成一个位置向量（或者叫位置嵌入，即position embedding,缩写为PE)；其次，这种编码并没有集成到模型本身中，该向量用于为每个单词提供有关其在句子中位置的信息，也就是说，其修改了模型的输入，添加了单词的顺序信息。

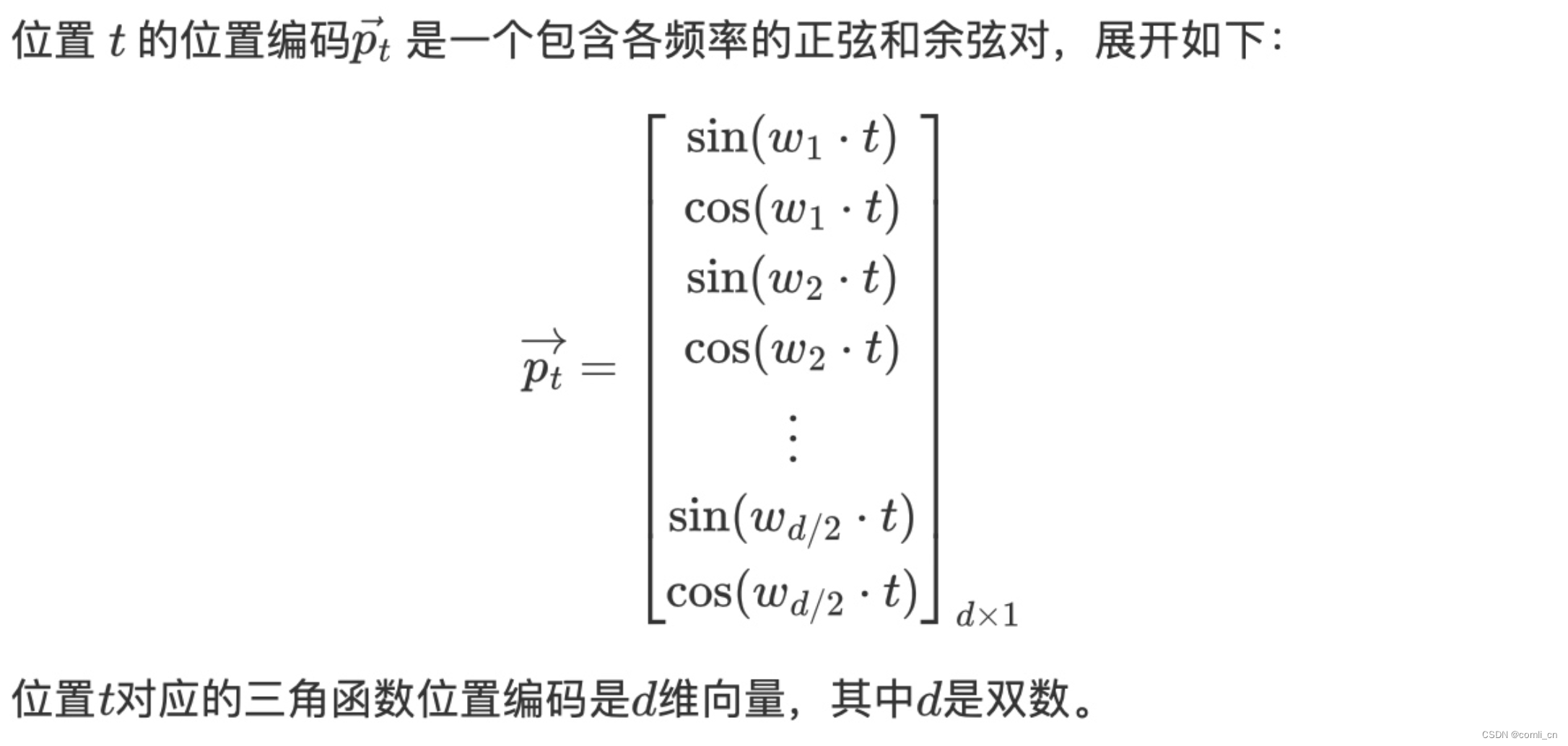
位置编码方式如下：

• 其中$d{\equiv }_{2}0$表示$d$ 被2整除之后余数为0
• $i$ 表示给某个token计算position embedding时是在embedding的第i位，从0开始
• 因为$sin(w_k\cdot t)$ 和 $cos(w_k\cdot t)$ 是一组，所以$k$ 是 $i$ 的二分之一

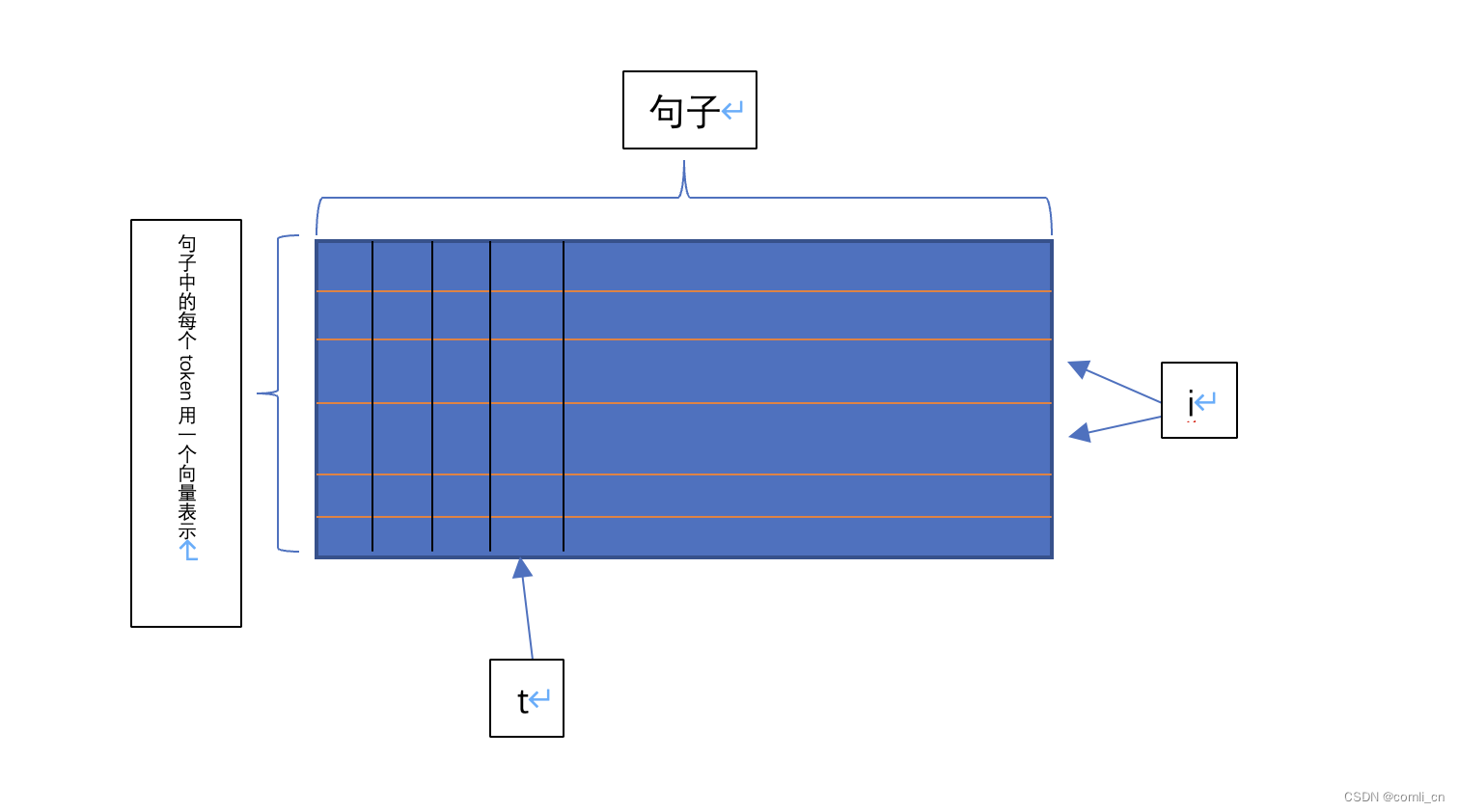
上图中长方形的宽度即为 $d$

4. 为什么要使用三角函数进行位置编码

• 可以使得不同位置的编码向量之间有一定的规律性，比如相邻位置之间的差异较小，而距离较远的位置之间的差异较大。

  这是由正弦和余弦函数的连续性和单调性保证的，即对于任意两个相邻的位置，它们对应的编码向量在每一个维度上都只有微小的变化，而对于任意两个距离较远的位置，它们对应的编码向量在每一个维度上都有较大的差异。

• 可以使得编码向量在任意维度上都能保持唯一性，即不同位置在同一个维度上不会有相同的值。

  这是由正弦和余弦函数的周期性和相位差保证的，即对于任意两个不同的位置，它们对应的编码向量在每一个维度上都不相等。

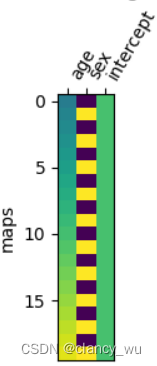
我们假设max_len为50， $d$ 取128，所以 $w$ 的取值范围就是0.0001～1，$t$ 的范围是0～49，所以三角函数自变量的取值范围是0～49，结果的取值范围为-1～1。则在 $t$ 为0时，对应的位置编码为[0, 1, 0, 1, 0, 1, ···, 0, 1]，这一点可以从下图的第一行看出来是0，1交替的。

相邻token位置编码每一位的 $w$ 相同只有 $t$ 相差1，由于三角函数的连续性，所以相邻token的位置编码值只有比很小的差别。

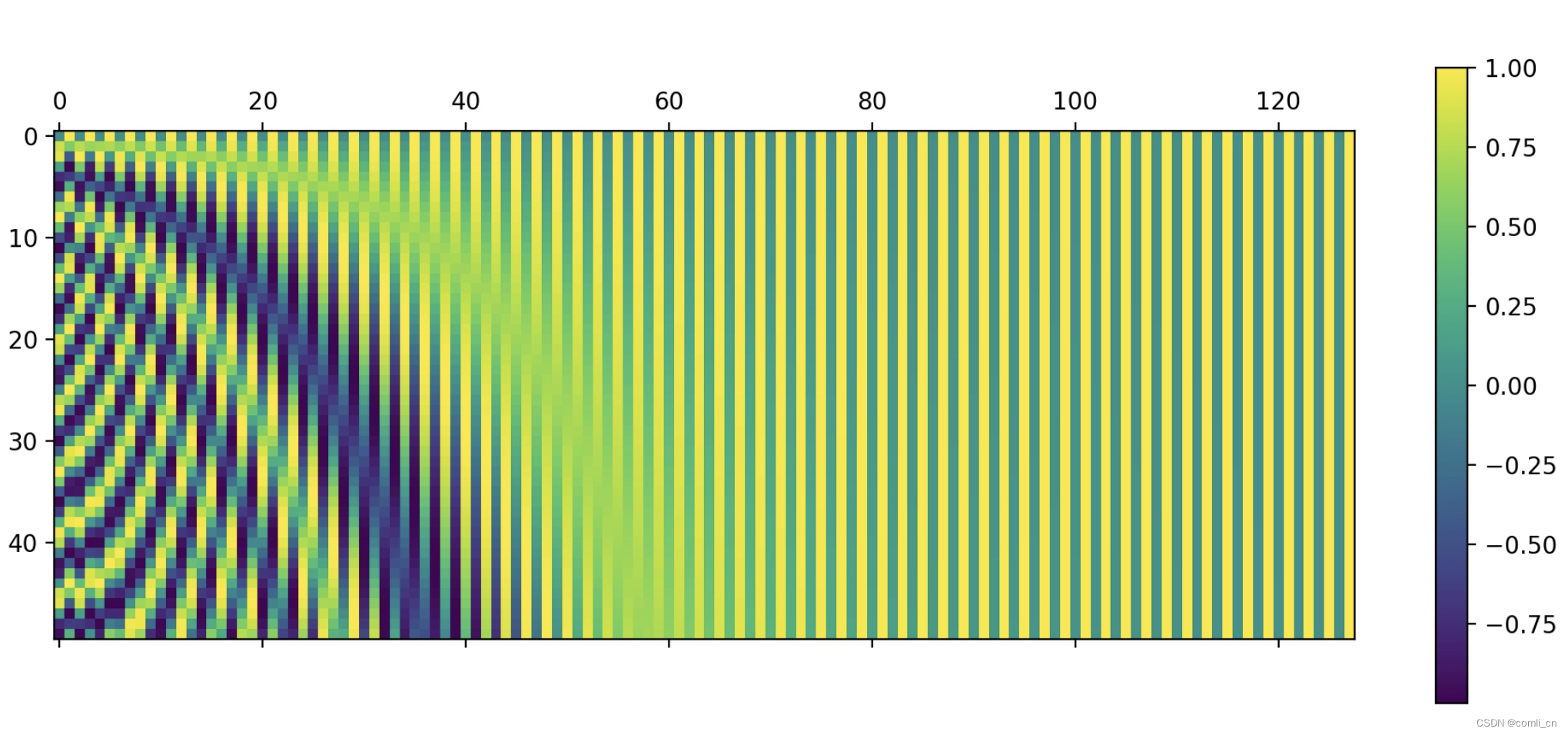
从上面效果图可以看出，这个三角函数式位置编码满足以下四个特点：

• 语句中每个词的位置编码是唯一的；
• 不同长度的句子中任意相邻两个词的间隔距离是一致的；
• 模型可以很容易处理更长的语句，并且值有界；
• 位置编码是确定性的。

参考：
Transformer 结构详解：位置编码 | Transformer Architecture: The Positional Encoding
理解Transformer的位置编码
什么？是Transformer位置编码