二叉树

递归法

迭代法

144. 二叉树的前序遍历 - 力扣（LeetCode）

二叉树的递归遍历

递归法作图分析

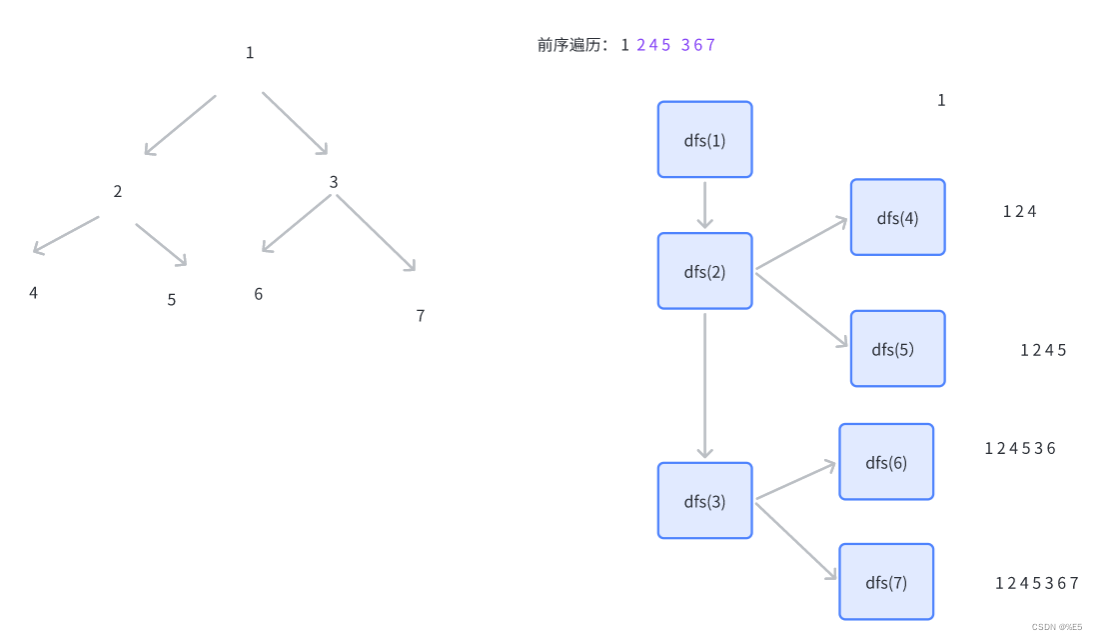
代码和思路分析

/**
* @param {TreeNode} root
* @return {number[]}
*/
var preorderTraversal = function(root) {
   /* 
       前序遍历：根左右
       我们用一个栈存入结果
       递归：顺序就是根左右，然后左右又分别是根，再根左右，循环，操作都一致了，可以使用递归
    */
   let res = []
   const dfs = function(root) {
       // 遇到空值，终止执行
       if(root === null) return;
       // 前序遍历从父节点开始
       res.push(root.val)
       // 之后会再压入左节点，右节点，然后每个节点的子节点，循环，使用递归
       // 左子树递归
       dfs(root.left)
       // 右子树递归
       dfs(root.right)
   }
   dfs(root)
   return res
};

二叉树的遍历除了递归还有迭代

二叉树的迭代遍历

非递归，遍历
用栈也可以实现前中后

前序遍历迭代分析

前序遍历是根左右
我们先让根节点入栈，然后让右节点入栈，再左节点
为什么先右后左？这样出栈的时候就可以达到根左右的效果
入栈：右–>左
出栈：根–>左–>右

代码及思路分析

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var preorderTraversal = function(root) {
    let res = []
    if(!root) return res
    // 把根节点存入栈中
    const stack = [root]
    let cur = null
    // 遍历栈里面的元素
    while(stack.length) {
        // 最开始出栈的是根节点root
        cur = stack.pop()
        // 把出栈的节点的值压入res存起来
        res.push(cur.val)
        // 然后分别把存在的右节点 左节点压入栈，之后循环，弹出左节点，右节点
        cur.right && stack.push(cur.right)
        cur.left && stack.push(cur.left)
    }
    return res
};

前序遍历解决了，中序遍历和后序遍历就好解决了

94. 二叉树的中序遍历

递归法

作图举例递归流程

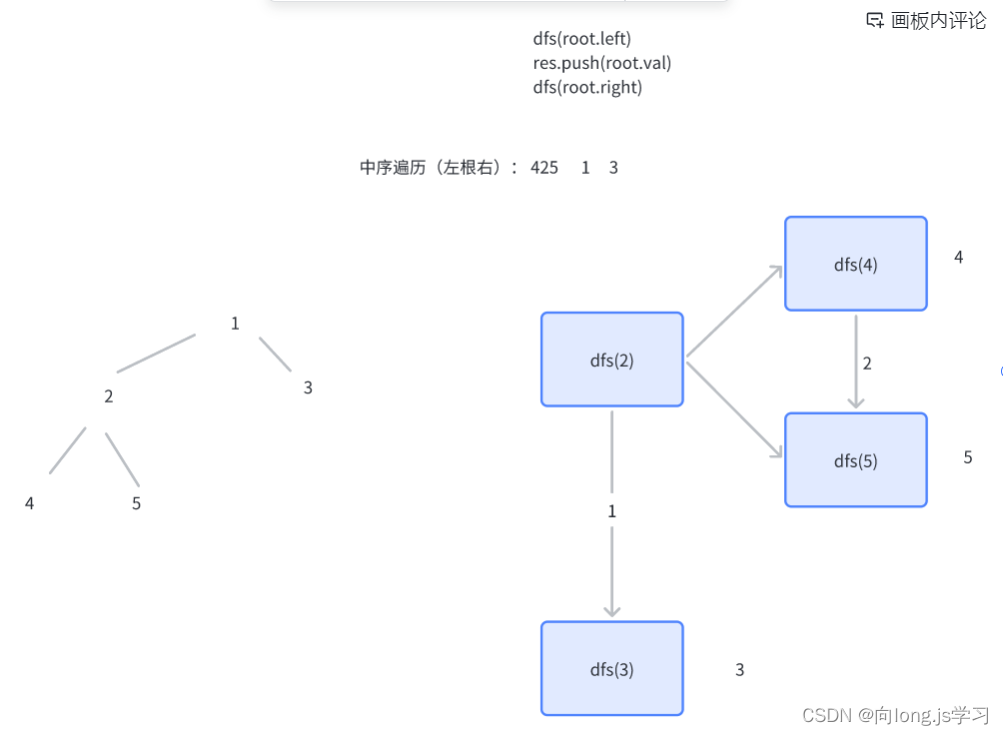
代码

/*
 * @lc app=leetcode.cn id=94 lang=javascript
 *
 * [94] 二叉树的中序遍历
 */

// @lc code=start
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var inorderTraversal = function(root) {
    /**
     * 中序遍历  递归左子树，压入根，递归右子树
     */
    let res = []
    const dfs = function(root) {
        if(root === null) return
        dfs(root.left)
        res.push(root.val)
        dfs(root.right)
    }
    dfs(root)
    return res
};
// @lc code=end

迭代法

迭代法分析

中序遍历：左根右
入栈：左 --> 右
出栈：左 --> 中 --> 右

代码

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var inorderTraversal = function(root) {
    let res = []
    const stack = []
    let cur = root
    while(stack.length || cur) { 
        /* 
            开始根节点存在，if语句执行，先让根节点入栈，然后让所有的左节点入栈
            当没有左节点的时候，执行else,弹出当前的末尾的左节点并且存入res中，再看右节点
         */
        if(cur) {
            // 根节点入栈
            stack.push(cur)
            // 左
            cur = cur.left
        } else {
            // 弹出
            cur = stack.pop()
            res.push(cur.val)
            // 右
            cur = cur.right
        }
    }
    return res
    
};

145. 二叉树的后序遍历 - 力扣（LeetCode）

递归法

/*
 * @lc app=leetcode.cn id=145 lang=javascript
 *
 * [145] 二叉树的后序遍历
 */

// @lc code=start
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var postorderTraversal = function(root) {
    /**
     * 后序遍历：左右根  左递归 右递归 压入根
     */
    let res = []
    const dfs = function(root) {
        if(root === null) return
        dfs(root.left)
        dfs(root.right)
        res.push(root.val)
    }
    dfs(root)
    return res
};
// @lc code=end

迭代法

入栈：左 --> 右
出栈： 中 --> 右 --> 左 结果翻转

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
 */
var postorderTraversal = function(root) {
    let res = []
    if(!root) return res
    const stack = [root]

    let cur = null

    do {
        cur = stack.pop()
        res.push(cur.val)
        cur.left && stack.push(cur.left)
        cur.right && stack.push(cur.right)
    } while(stack.length)
    return res.reverse()
};

好多问题画图就可以迎刃而解
算法一遍不熟，大不了就多刷一遍，我都第三遍了

二叉树的统一迭代法

二叉树：一入递归深似海，从此offer是路人
递归至今我还不会？！！

前序遍历统一的迭代法

// 前序遍历：中左右
// 压栈顺序：右左中

var preorderTraversal = function(root, res = []) {
   const stack = [];
   if (root) stack.push(root);
   while(stack.length) {
       const node = stack.pop();
       if(!node) {
           res.push(stack.pop().val);
           continue;
       }
       if (node.right) stack.push(node.right); // 右
       if (node.left) stack.push(node.left); // 左
       stack.push(node); // 中
       stack.push(null);
   };
   return res;
};

中序遍历统一的迭代法

//  中序遍历：左中右
//  压栈顺序：右中左
 
var inorderTraversal = function(root, res = []) {
    const stack = [];
    if (root) stack.push(root);
    while(stack.length) {
        const node = stack.pop();
        if(!node) {
            res.push(stack.pop().val);
            continue;
        }
        if (node.right) stack.push(node.right); // 右
        stack.push(node); // 中
        stack.push(null);
        if (node.left) stack.push(node.left); // 左
    };
    return res;
};

后序遍历统一的迭代法

// 后续遍历：左右中
// 压栈顺序：中右左
 
var postorderTraversal = function(root, res = []) {
    const stack = [];
    if (root) stack.push(root);
    while(stack.length) {
        const node = stack.pop();
        if(!node) {
            res.push(stack.pop().val);
            continue;
        }
        stack.push(node); // 中
        stack.push(null);
        if (node.right) stack.push(node.right); // 右
        if (node.left) stack.push(node.left); // 左
    };
    return res;
};