[面试题]:判断二维空间中一点是否在旋转矩形内部
参考:
1. 判断点是否在一个矩形内
2. 向量点乘与叉乘的概念及几何意义
3. 向量叉乘
4. 向量叉乘的正负意义
5. 本工程完整代码
题目描述
已知条件:旋转矩形中心center(x,y), 旋转矩形的长l 和 宽w, 以及与X轴旋转角度theta。
返回值: 是否在其内部,即返回是/否。
一. 主要介绍两种方法
1.1 面积法
每一个点到矩形任意两个顶点组成三角形面积,共有四个△,判断它们面积之和是否等于矩形的面积。
// 计算三角形面积
double CalculateTriangleArea(const Point& a, const Point& b, const Point& c){
// 向量叉乘x1y2-x2y1的大小的一半
double res = 0;
if((a.x == b.x && a.y == b.y )|| (a.x == c.x && a.y == c.y )|| (b.x == c.x && b.y == c.y)) return res;
Vector2d ba(a.x -b.x, a.y - b.y);
Vector2d bc(c.x -b.x, c.y - b.y);
res = fabs(ba.x*bc.y - bc.x*ba.y) * 0.5;
return res;
}
// 旋转矩形4个角点ABCD
Point A(cloud.points[0].x, cloud.points[0].y);
Point B(cloud.points[1].x, cloud.points[1].y);
Point C(cloud.points[2].x, cloud.points[2].y);
Point D(cloud.points[3].x, cloud.points[3].y);
// 法一: 面积法, 分别计算点p与矩形四个边组成的面积,求和
auto area1 = CalculateTriangleArea(A, B, p);
auto area2 = CalculateTriangleArea(B, C, p);
auto area3 = CalculateTriangleArea(C, D, p);
auto area4 = CalculateTriangleArea(D, A, p);
if(fabs(area1+area2+area3+area4 - w*h)< 1e-3) return true;
else return false;
1.2 叉乘的方向性
只需要判断该点是否在上下两条边和左右两条边之间就行。从向量叉乘的方向性考虑,叉积( x 1 , y 1 ) × ( x 2 , y 2 ) = x 1 ∗ y 2 − x 2 ∗ y 1,大小表示两个向量围成的平行四边形的面积,正负表示两个向量的相对位置
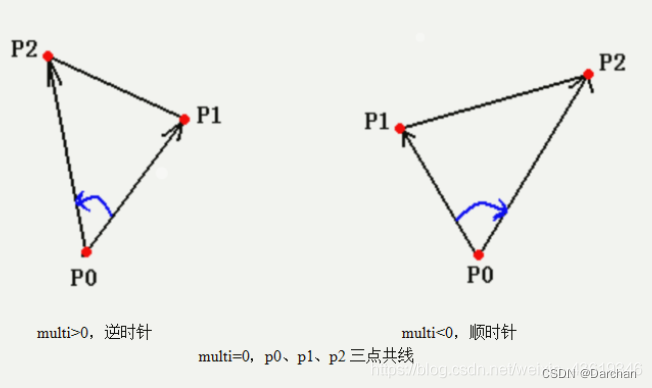
// 法二: 向量方向性, 满足(BA*Bp)(DC*Dp)>=0,先叉乘,利用叉乘正负判断方向,矩形对面所夹着的点方向相同
Vector2d BA(A.x -B.x, A.y - B.y);
Vector2d Bp(p.x -B.x, p.y - B.y);
Vector2d DC(C.x -D.x, C.y - D.y);
Vector2d Dp(p.x -D.x, p.y - D.y);
/* 若严格按照ABCD顺序来,两个数都是大于0,乘积的方式是顾忌到矩形4个顶点的ABCD顺时针排序还是逆时针排序 */
auto val1 = (BA.x * Bp.y - Bp.x * BA.y) * (DC.x * Dp.y - Dp.x * DC.y);
Vector2d DA(D.x -A.x, D.y - A.y);
Vector2d BC(B.x -C.x, B.y - C.y);
auto val2 = (DA.x * Dp.y - Dp.x * DA.y)* (BC.x * Bp.y - Bp.x * BC.y);
if(val1 >=0 && val2 >=0) return true;
else return false;
二. OpenCV添加了可视化效果
效果如下图,方便调试,查看结果。
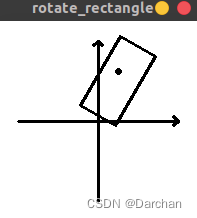
// 绘制箭头
void DrawArrow(cv::Mat &img, cv::Point pStart, cv::Point pEnd, int len,
int alpha, cv::Scalar &color, int thickness, int lineType) {
cv::Point arrow;
double angle =
atan2((double)(pStart.y - pEnd.y), (double)(pStart.x - pEnd.x));
cv::line(img, pStart, pEnd, color, thickness, lineType);
arrow.x = pEnd.x + len * cos(angle + PI * alpha / 180);
arrow.y = pEnd.y + len * sin(angle + PI * alpha / 180);
cv::line(img, pEnd, arrow, color, thickness, lineType);
arrow.x = pEnd.x + len * cos(angle - PI * alpha / 180);
arrow.y = pEnd.y + len * sin(angle - PI * alpha / 180);
cv::line(img, pEnd, arrow, color, thickness, lineType);
}
// Debug: 绘制旋转矩形和待测试点
void DrawRotateRectangle(const pcl::PointCloud<pcl::PointXYZ>& cloud, const Point& p){
int img_x = 200, img_y = 200;
cv::Scalar arrow_color = cv::Scalar(0, 0, 0);
cv::Mat img(img_y, img_x, CV_8UC3, cv::Scalar(255, 255, 255));
DrawArrow(img, cv::Point(img_x/2.0, img_y -20),
cv::Point(img_x/2.0, 20), 6, 45, arrow_color, 2, 8);
DrawArrow(img, cv::Point(20, img_y/2.0),
cv::Point(img_x-20, img_y/2.0), 6, 45, arrow_color, 2, 8);
for(int i=0; i<4; ++i){
if(i < 3){
cv::line(img, cv::Point(cloud.points[i].x+100, -cloud.points[i].y+100), cv::Point(cloud.points[i+1].x+100, -cloud.points[i+1].y+100), arrow_color, 2, 8);
}else{
cv::line(img, cv::Point(cloud.points[i].x+100, -cloud.points[i].y+100), cv::Point(cloud.points[0].x+100, -cloud.points[0].y+100), arrow_color, 2, 8);
}
}
cv::circle(img, cv::Point(p.x+100, -p.y+100), 2, arrow_color, 2, 8);
cv::imshow("rotate_rectangle", img);
cv::waitKey(0);
}
三. 利用中心center,长宽,theta还原四个角点坐标
// 还原4个角点坐标
pcl::PointCloud<pcl::PointXYZ> cloud;
cloud.points.emplace_back(pcl::PointXYZ(-w/2.0, h/2.0, 0));
cloud.points.emplace_back(pcl::PointXYZ(-w/2.0, -h/2.0, 0));
cloud.points.emplace_back(pcl::PointXYZ(w/2.0, -h/2.0, 0));
cloud.points.emplace_back(pcl::PointXYZ(w/2.0, h/2.0, 0));
// DrawRotateRectangle(cloud, p);
Eigen::Matrix4d mat = Eigen::Matrix4d::Identity();
// 旋转矩阵形式
mat << cos(theta*PI/ 180.0), -sin(theta*PI/ 180.0), 0, center.x,
sin(theta*PI/ 180.0), cos(theta*PI/ 180.0), 0, center.y,
0, 0, 1, 0,
0, 0, 0, 1 ;
std::cout << "mat: " << mat << std::endl;
pcl::transformPointCloud(cloud, cloud, mat);