文章目录
- 参考资料
- 前言
- 推导
- 先x方向,后y方向
- 先y方向,后x方向
- 简化后的双线性插值
- 双线性插值的一阶导
参考资料
- https://en.wikipedia.org/wiki/Bilinear_interpolation
前言
双线性插值,又称为双线性内插。在数学上,双线性插值是对线性插值在二维直角网格上的扩展,用于对双变量函数(例如 x 和 y)进行插值。其核心思想是在x,y两个方向分别进行一次线性插值。
线性插值可以查看 之前的博客文章。
推导
假如我们想得到未知函数 f f f 在点 P = ( x , y ) P=(x, y) P=(x,y) 的值,假设我们已知函数 f f f 在 Q 11 = ( x 1 , y 1 ) , Q 12 = ( x 1 , y 2 ) , Q 21 = ( x 2 , y 1 ) Q_{11}=\left(x_1, y_1\right) , Q_{12}=\left(x_1, y_2\right) , Q_{21}=\left(x_2, y_1\right) Q11=(x1,y1),Q12=(x1,y2),Q21=(x2,y1) , Q 22 = ( x 2 , y 2 ) Q_{22}=\left(x_2, y_2\right) Q22=(x2,y2) 四个点的值。
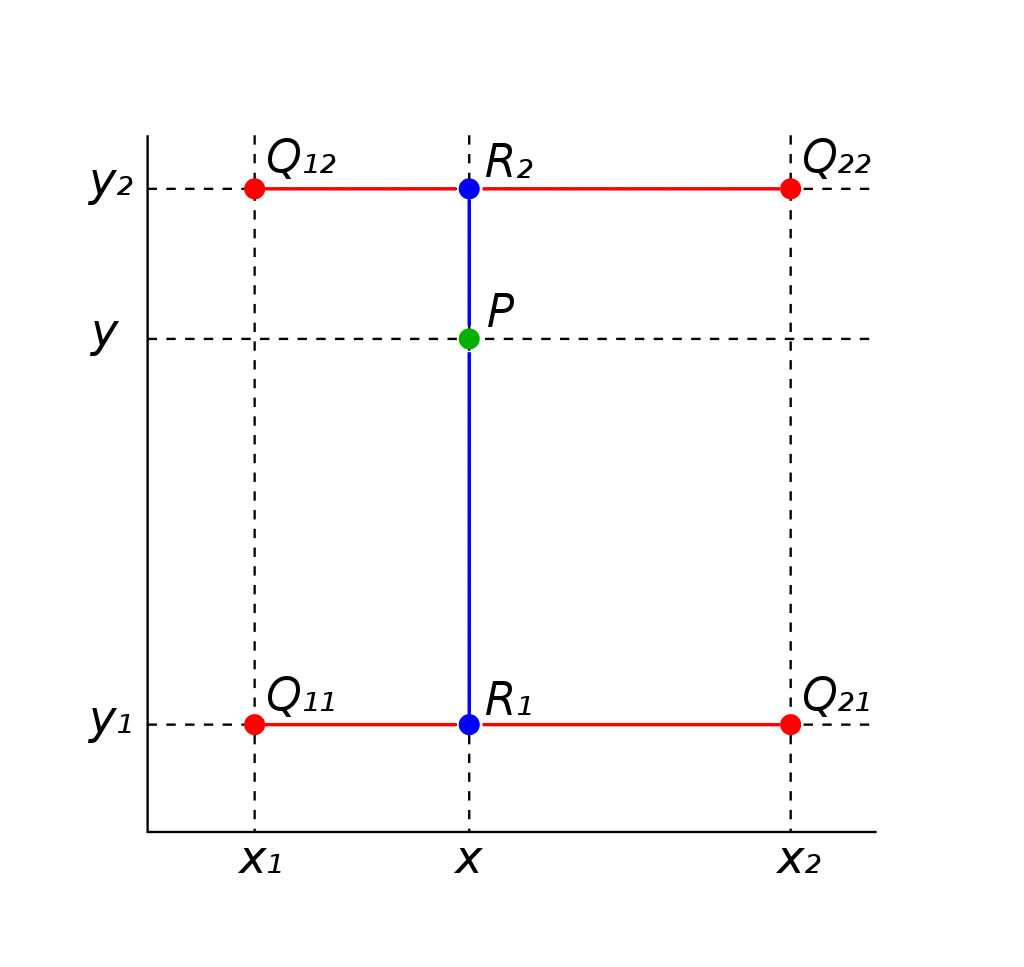
先x方向,后y方向
首先在
x
x
x 方向进行线性插值 (即
x
x
x变,
y
y
y不变),得到
f
(
x
,
y
1
)
≈
x
2
−
x
x
2
−
x
1
f
(
Q
11
)
+
x
−
x
1
x
2
−
x
1
f
(
Q
21
)
,
f
(
x
,
y
2
)
≈
x
2
−
x
x
2
−
x
1
f
(
Q
12
)
+
x
−
x
1
x
2
−
x
1
f
(
Q
22
)
.
\begin{aligned} & f\left(x, y_1\right) \approx \frac{x_2-x}{x_2-x_1} f\left(Q_{11}\right)+\frac{x-x_1}{x_2-x_1} f\left(Q_{21}\right), \\ & f\left(x, y_2\right) \approx \frac{x_2-x}{x_2-x_1} f\left(Q_{12}\right)+\frac{x-x_1}{x_2-x_1} f\left(Q_{22}\right) . \end{aligned}
f(x,y1)≈x2−x1x2−xf(Q11)+x2−x1x−x1f(Q21),f(x,y2)≈x2−x1x2−xf(Q12)+x2−x1x−x1f(Q22).
然后在
y
y
y 方向进行线性插值,得到
f
(
x
,
y
)
≈
y
2
−
y
y
2
−
y
1
f
(
x
,
y
1
)
+
y
−
y
1
y
2
−
y
1
f
(
x
,
y
2
)
=
y
2
−
y
y
2
−
y
1
(
x
2
−
x
x
2
−
x
1
f
(
Q
11
)
+
x
−
x
1
x
2
−
x
1
f
(
Q
21
)
)
+
y
−
y
1
y
2
−
y
1
(
x
2
−
x
x
2
−
x
1
f
(
Q
12
)
+
x
−
x
1
x
2
−
x
1
f
(
Q
22
)
)
=
1
(
x
2
−
x
1
)
(
y
2
−
y
1
)
(
f
(
Q
11
)
(
x
2
−
x
)
(
y
2
−
y
)
+
f
(
Q
21
)
(
x
−
x
1
)
(
y
2
−
y
)
+
f
(
Q
12
)
(
x
2
−
x
)
(
y
−
y
1
)
+
f
(
Q
22
)
(
x
−
x
1
)
(
y
−
y
1
)
)
=
1
(
x
2
−
x
1
)
(
y
2
−
y
1
)
[
x
2
−
x
x
−
x
1
]
[
f
(
Q
11
)
f
(
Q
12
)
f
(
Q
21
)
f
(
Q
22
)
]
[
y
2
−
y
y
−
y
1
]
.
\begin{aligned} f(x, y) & \approx \frac{y_2-y}{y_2-y_1} f\left(x, y_1\right)+\frac{y-y_1}{y_2-y_1} f\left(x, y_2\right) \\ & =\frac{y_2-y}{y_2-y_1}\left(\frac{x_2-x}{x_2-x_1} f\left(Q_{11}\right)+\frac{x-x_1}{x_2-x_1} f\left(Q_{21}\right)\right)+\frac{y-y_1}{y_2-y_1}\left(\frac{x_2-x}{x_2-x_1} f\left(Q_{12}\right)+\frac{x-x_1}{x_2-x_1} f\left(Q_{22}\right)\right) \\ & =\frac{1}{\left(x_2-x_1\right)\left(y_2-y_1\right)}\left(f\left(Q_{11}\right)\left(x_2-x\right)\left(y_2-y\right)+f\left(Q_{21}\right)\left(x-x_1\right)\left(y_2-y\right)+f\left(Q_{12}\right)\left(x_2-x\right)\left(y-y_1\right)+f\left(Q_{22}\right)\left(x-x_1\right)\left(y-y_1\right)\right) \\ & =\frac{1}{\left(x_2-x_1\right)\left(y_2-y_1\right)}\left[x_2-x \quad x-x_1\right]\left[\begin{array}{ll} f\left(Q_{11}\right) & f\left(Q_{12}\right) \\ f\left(Q_{21}\right) & f\left(Q_{22}\right) \end{array}\right]\left[\begin{array}{l} y_2-y \\ y-y_1 \end{array}\right] . \end{aligned}
f(x,y)≈y2−y1y2−yf(x,y1)+y2−y1y−y1f(x,y2)=y2−y1y2−y(x2−x1x2−xf(Q11)+x2−x1x−x1f(Q21))+y2−y1y−y1(x2−x1x2−xf(Q12)+x2−x1x−x1f(Q22))=(x2−x1)(y2−y1)1(f(Q11)(x2−x)(y2−y)+f(Q21)(x−x1)(y2−y)+f(Q12)(x2−x)(y−y1)+f(Q22)(x−x1)(y−y1))=(x2−x1)(y2−y1)1[x2−xx−x1][f(Q11)f(Q21)f(Q12)f(Q22)][y2−yy−y1].
先y方向,后x方向
首先在
y
y
y 方向进行线性插值 (即
y
y
y变,
x
x
x不变),得到
f
(
x
1
,
y
)
≈
y
2
−
y
y
2
−
y
1
f
(
Q
11
)
+
y
−
y
1
y
2
−
y
1
f
(
Q
12
)
,
f
(
x
2
,
y
)
≈
y
2
−
y
y
2
−
y
1
f
(
Q
21
)
+
y
−
y
1
y
2
−
y
1
f
(
Q
22
)
.
\begin{aligned} & f\left(x_1, y\right) \approx \frac{y_2-y}{y_2-y_1} f\left(Q_{11}\right)+\frac{y-y_1}{y_2-y_1} f\left(Q_{12}\right), \\ & f\left(x_2, y\right) \approx \frac{y_2-y}{y_2-y_1} f\left(Q_{21}\right)+\frac{y-y_1}{y_2-y_1} f\left(Q_{22}\right) . \end{aligned}
f(x1,y)≈y2−y1y2−yf(Q11)+y2−y1y−y1f(Q12),f(x2,y)≈y2−y1y2−yf(Q21)+y2−y1y−y1f(Q22).
然后在
x
x
x 方向进行线性插值,得到
f
(
x
,
y
)
≈
x
2
−
x
x
2
−
x
1
f
(
x
1
,
y
)
+
x
−
x
1
x
2
−
x
1
f
(
x
2
,
y
)
=
x
2
−
x
x
2
−
x
1
(
y
2
−
y
y
2
−
y
1
f
(
Q
11
)
+
y
−
y
1
y
2
−
y
1
f
(
Q
12
)
)
+
x
−
x
1
x
2
−
x
1
(
y
2
−
y
y
2
−
y
1
f
(
Q
21
)
+
y
−
y
1
y
2
−
y
1
f
(
Q
22
)
)
=
1
(
x
2
−
x
1
)
(
y
2
−
y
1
)
(
f
(
Q
11
)
(
x
2
−
x
)
(
y
2
−
y
)
+
f
(
Q
21
)
(
x
−
x
1
)
(
y
2
−
y
)
+
f
(
Q
12
)
(
x
2
−
x
)
(
y
−
y
1
)
+
f
(
Q
22
)
(
x
−
x
1
)
(
y
−
y
1
)
)
=
1
(
x
2
−
x
1
)
(
y
2
−
y
1
)
[
x
2
−
x
x
−
x
1
]
[
f
(
Q
11
)
f
(
Q
12
)
f
(
Q
21
)
f
(
Q
22
)
]
[
y
2
−
y
y
−
y
1
]
.
\begin{aligned} f(x, y) & \approx \frac{x_2-x}{x_2-x_1} f\left(x_1, y\right)+\frac{x-x_1}{x_2-x_1} f\left(x_2, y\right) \\ & =\frac{x_2-x}{x_2-x_1}\left(\frac{y_2-y}{y_2-y_1} f\left(Q_{11}\right)+\frac{y-y_1}{y_2-y_1} f\left(Q_{12}\right)\right)+\frac{x-x_1}{x_2-x_1}\left(\frac{y_2-y}{y_2-y_1} f\left(Q_{21}\right)+\frac{y-y_1}{y_2-y_1} f\left(Q_{22}\right)\right) \\ & =\frac{1}{\left(x_2-x_1\right)\left(y_2-y_1\right)}\left(f\left(Q_{11}\right)\left(x_2-x\right)\left(y_2-y\right)+f\left(Q_{21}\right)\left(x-x_1\right)\left(y_2-y\right)+f\left(Q_{12}\right)\left(x_2-x\right)\left(y-y_1\right)+f\left(Q_{22}\right)\left(x-x_1\right)\left(y-y_1\right)\right) \\ & =\frac{1}{\left(x_2-x_1\right)\left(y_2-y_1\right)}\left[x_2-x \quad x-x_1\right]\left[\begin{array}{ll} f\left(Q_{11}\right) & f\left(Q_{12}\right) \\ f\left(Q_{21}\right) & f\left(Q_{22}\right) \end{array}\right]\left[\begin{array}{l} y_2-y \\ y-y_1 \end{array}\right] . \end{aligned}
f(x,y)≈x2−x1x2−xf(x1,y)+x2−x1x−x1f(x2,y)=x2−x1x2−x(y2−y1y2−yf(Q11)+y2−y1y−y1f(Q12))+x2−x1x−x1(y2−y1y2−yf(Q21)+y2−y1y−y1f(Q22))=(x2−x1)(y2−y1)1(f(Q11)(x2−x)(y2−y)+f(Q21)(x−x1)(y2−y)+f(Q12)(x2−x)(y−y1)+f(Q22)(x−x1)(y−y1))=(x2−x1)(y2−y1)1[x2−xx−x1][f(Q11)f(Q21)f(Q12)f(Q22)][y2−yy−y1].
可见,无论哪个方向先进行插值,双线性插值的结果是一样的。
简化后的双线性插值
如果选择一个坐标系统使得
f
f
f 的四个已知点坐标分别为
(
x
1
,
y
1
)
=
(
0
,
0
)
、
(
x
1
,
y
2
)
=
(
0
,
1
)
、
(
x
2
,
y
1
)
=
(
1
,
0
)
(x_1,y_1)=(0,0) 、(x_1,y_2)=(0,1) 、(x_2,y_1)=(1,0)
(x1,y1)=(0,0)、(x1,y2)=(0,1)、(x2,y1)=(1,0) 和
(
x
2
,
y
2
)
=
(
1
,
1
)
(x_2,y_2)=(1,1)
(x2,y2)=(1,1) ,那么插值公式就可以化简为
f
(
x
,
y
)
≈
f
(
0
,
0
)
(
1
−
x
)
(
1
−
y
)
+
f
(
1
,
0
)
x
(
1
−
y
)
+
f
(
0
,
1
)
(
1
−
x
)
y
+
f
(
1
,
1
)
x
y
≈
[
1
−
x
x
]
[
f
(
0
,
0
)
f
(
0
,
1
)
f
(
1
,
0
)
f
(
1
,
1
)
]
[
1
−
y
y
]
\begin{aligned} f(x, y) &\approx f(0,0)(1-x)(1-y)+f(1,0) x(1-y)+f(0,1)(1-x) y+f(1,1) x y \\ & \approx\left[\begin{array}{ll} 1-x & x \end{array}\right]\left[\begin{array}{ll} f(0,0) & f(0,1) \\ f(1,0) & f(1,1) \end{array}\right]\left[\begin{array}{c} 1-y \\ y \end{array}\right] \end{aligned}
f(x,y)≈f(0,0)(1−x)(1−y)+f(1,0)x(1−y)+f(0,1)(1−x)y+f(1,1)xy≈[1−xx][f(0,0)f(1,0)f(0,1)f(1,1)][1−yy]
双线性插值的一阶导
在进行code reading 时,发现有时候会需要计算插值后的结果在x,y方向上的一阶导,因此,这里也给出双线性插值的一阶导。
f
(
x
,
y
)
f(x,y)
f(x,y)在
x
x
x方向上的一阶导:
∂
f
∂
x
=
1
(
x
2
−
x
1
)
(
y
2
−
y
1
)
[
−
1
1
]
[
f
(
Q
11
)
f
(
Q
12
)
f
(
Q
21
)
f
(
Q
22
)
]
[
y
2
−
y
y
−
y
1
]
.
\frac{\partial f}{\partial x}=\frac{1}{\left(x_2-x_1\right)\left(y_2-y_1\right)}\left[-1 \quad 1\right]\left[\begin{array}{ll} f\left(Q_{11}\right) & f\left(Q_{12}\right) \\ f\left(Q_{21}\right) & f\left(Q_{22}\right) \end{array}\right]\left[\begin{array}{l} y_2-y \\ y-y_1 \end{array}\right] .
∂x∂f=(x2−x1)(y2−y1)1[−11][f(Q11)f(Q21)f(Q12)f(Q22)][y2−yy−y1].
f ( x , y ) f(x,y) f(x,y)在 y y y方向上的一阶导:
∂ f ∂ y = 1 ( x 2 − x 1 ) ( y 2 − y 1 ) [ x 2 − x x − x 1 ] [ f ( Q 11 ) f ( Q 12 ) f ( Q 21 ) f ( Q 22 ) ] [ − 1 1 ] . \frac{\partial f}{\partial y}=\frac{1}{\left(x_2-x_1\right)\left(y_2-y_1\right)}\left[x_2-x \quad x-x_1\right]\left[\begin{array}{ll} f\left(Q_{11}\right) & f\left(Q_{12}\right) \\ f\left(Q_{21}\right) & f\left(Q_{22}\right) \end{array}\right]\left[\begin{array}{l} -1 \\ 1 \end{array}\right] . ∂y∂f=(x2−x1)(y2−y1)1[x2−xx−x1][f(Q11)f(Q21)f(Q12)f(Q22)][−11].
简化后:
∂ f ∂ x = [ − 1 , 1 ] [ f ( 0 , 0 ) f ( 0 , 1 ) f ( 1 , 0 ) f ( 1 , 1 ) ] [ 1 − y y ] \frac{\partial f}{\partial x}=[-1,1]\left[\begin{array}{ll} f(0,0) & f(0,1) \\ f(1,0) & f(1,1) \end{array}\right]\left[\begin{array}{c} 1-y \\ y \end{array}\right] ∂x∂f=[−1,1][f(0,0)f(1,0)f(0,1)f(1,1)][1−yy]
∂ f ∂ y = [ 1 − x , x ] [ f ( 0 , 0 ) f ( 0 , 1 ) f ( 1 , 0 ) f ( 1 , 1 ) ] [ − 1 1 ] \frac{\partial f}{\partial y}=[1-x, x]\left[\begin{array}{ll} f(0,0) & f(0,1) \\ f(1,0) & f(1,1) \end{array}\right]\left[\begin{array}{c} -1 \\ 1 \end{array}\right] ∂y∂f=[1−x,x][f(0,0)f(1,0)f(0,1)f(1,1)][−11]
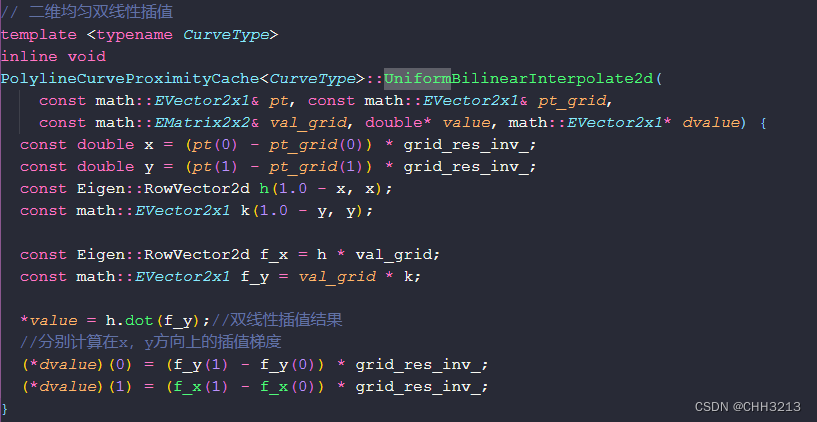
c++实现参考如下: