目录
2.2.1 什么是堆栈
堆栈
什么是堆栈
例子:计算机如何进行表达式求值?如:5+6/2-3*4
后缀表达式
堆栈的抽象数据类型描述
2.2.2 堆栈的顺序存储实现
例子:用一个数组实现两个堆栈,要求能最大利用数组空间,只要有空间就能实现入栈
2.2.3 堆栈的链式存储实现
2.2.4 堆栈应用:表达式求值
中缀表达式如何转换为后缀表达式
其他用途
2.2.1 什么是堆栈
堆栈
概念:一种线性结构,也是特殊的线性表
用途:表达式求值、递归、函数调用等实际上是使用堆栈实现的
什么是堆栈
例子:计算机如何进行表达式求值?如:5+6/2-3*4
如果没有优先级顺序,从左向右计算即可。表达式求值需要的是运算符和运算符前后的两个算子。而通常情况下运算符之后的数字并不一定是算子,而是需要运算的表达式。然而如果已知两个算子,那么接下来的计算就比较简单了。我们就引入了后缀表达式。
后缀表达式
概念:运算符号在运算数之后。
处理逻辑:遇到运算数先放着,遇到运算符就把最近存放的两个数拿来和运算符做运算。
我们通常使用的表达式是中缀表达式,即a+b*c-d/e,运算符号位于两个运算数中间。
与之等价的后缀表达式是:abc*+de/-(等价的前缀表达式:-+a*bc/de)
后缀表达式的这种处理逻辑,再抽象一下就是:一种能够存储运算数,并且先存储的后处理(后存储的先处理),像一口井一样的存储结构,我们称其为:堆栈
堆栈的抽象数据类型描述
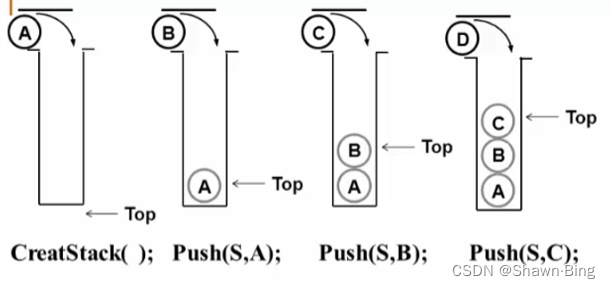
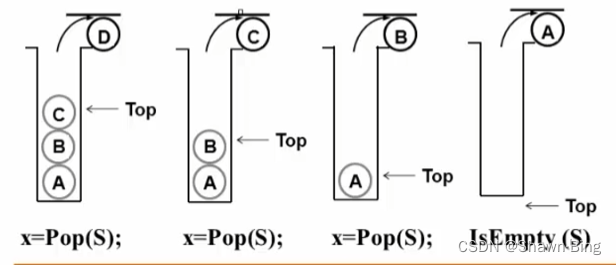
堆栈(Stack):具有一定操作约束的线性表——只能在一端(称为栈顶,top)做插入和删除操作
- 插入数据:入栈(Push)
- 删除数据:出栈(Pop)
- 处理顺序:后入先出(Last In First Out——LIFO)
- 数据对象集:0~N个元素的有穷线性表
- 操作集:长度为MaxSize的堆栈S(S属于Stack),堆栈元素item(item属于ElementType)
- Stack CreateStack(int MaxSize) 生成一个空堆栈,最大长度为MaxSize
- int IsFull(Stack S,int MaxSize) 判断堆栈是否已满
- void Push(Stack S,ElementType item) 将元素item压入堆栈
- int IsEmpty(Stack S) 判断堆栈是否为空
- ElementType Pop(Stack S) 删除并返回栈顶元素
2.2.2 堆栈的顺序存储实现
栈的顺序存储结构实现一般使用一个结构体——包含一个一维数组和一个记录站定元素位置的变量组成。(和线性表比较像,像啊,很像啊,但是还记得吗?线性表的int元素是为了记录表长,这一点稍微不一样)
#define MaxSize //定义存储元素最大值
typedef struct SNode *Stack;
struct SNode{
ElementType Data[MaxSize];
int Top;
};//1.入栈
void Push(Stack PrtS,ElementType item)
{
//用数组存储,当top指向max-1时说明已满
if( PrtS->Top == MaxSize-1 ){
printf("堆栈已满");
return;
}else{
//top位置增加,然后将元素放入
PrtS->Data[++(PrtS->Top)] = item;
return;
}
}//2.出栈
ElementType Pop(Stack PtrS)
{
//若指向-1,说明栈空
if(PtrS->Top == -1){
printf("堆栈空");
return ERROR;
}else{
//1.返回下标为Top的值
//2.将Top值-1
return(PtrS->Data[(PtrS->Top)--]);
}
}例子:用一个数组实现两个堆栈,要求能最大利用数组空间,只要有空间就能实现入栈
如何做?一个数组,两头都作为栈顶,左边要插入元素就将栈底向右,删除元素就删除先从最左元素开始。右边同理。
那么如何进行其他的操作集?比如如何判断堆栈已满?
两个栈肯定是需要两个栈顶的,而当两个栈顶相遇的时候,就说明栈已满。
对于栈空的判断,左栈顶设为Top1,右栈顶设为Top2。那么S.Top1=-1时左栈空。S.Top2=MaxSize(栈顶=MaxSize-1时说明右栈有一个元素)时右栈空。
这样的堆栈Push操作如下:
void Push(Struct DStack *PtrS,ElementType item, int Tag){
//Tag用于区别两个堆栈,分别取1和2
//两个栈相遇,说明相减等于1
if(PtrS->Top2 - PtrS->Top1 == 1){
printf("堆栈已满");
}
if(Tag == 1){
//插入栈1,放到top1后
PtrS->Data[++(PtrS->Top1)] = item;
}else{
//插入栈2,放到top2前
PtrS->Data[--(PtrS->Top2)] = item;
}
}ElementType Pop(Struct DStack *PtrS, int Tag){
//删除栈1元素
if(Tag == 1){
//判断栈1是否空
if(PtrS->Top1 == -1){
printf("堆栈1空");
return NULL;
}else{
//top1向左挪
return PtrS->Data[(PtrS->Top1)--];
}
//删除栈2元素
}else{
if(PtrS->Top2 == MaxSize){
printf("堆栈2空");
return NULL;
}else{
//top2向左挪
return PtrS->Data[(PtrS->Top2)++];
}
}2.2.3 堆栈的链式存储实现
堆栈的链式存储结构通常用单链表来实现,称为链栈。插入和删除操作只能在链栈的栈顶进行。
栈顶指针Top位于链表头。因为链表尾删除操作没法完成,找不到上一个节点的位置(链表的局限性)
typedef struct SNode *Stack;
struct SNode{
ElementType Data;
struct SNode *Next;
};
//1.初始化堆栈
Stack CreateStack()
{
Stack S;
//申请节点
S = (Stack)malloc(sizeof(struct SNode));
S->Next = NULL;
return S;
}
int IsEmpty(Stack S)
{
//若为空返回1,非空返回0
return (S->Next == NULL);
}//2.Push,相当于向链表中第一个元素前插入元素
void Push(ElementType item, Stack S){
struct SNode *TempCell;
TempCell = (struct SNode *)malloc(sizeof(struct SNode));
TempCell -> Element = item;
TempCell -> Next = S->Next;
S->Next = TempCell;
}
//3.Pop,需要判断是否为空,相当于删除头结点后的第一个结点
ElementType Pop(Stack S){
struct SNode *FirstCell;
ElementType TopElem;
if(IsEmpty(S)){
printf("堆栈空");
return NULL;
}else{
FirstCell = S->Next;//暂存,为了释放
S->Next = FirstCell->Next;
TopElem = FirstCell->Element;
free(FirstCell);
return TopElem;
}
}2.2.4 堆栈应用:表达式求值
前文提到,可以使用堆栈来实现后缀表达式求值的基本过程。那么如何用堆栈求中缀表达式呢?
简单来说,直接将中缀表达式转换为后缀表达式,再求值。但是如何将中缀转换为后缀?
eg:2+9/3-5(中缀) -> 293/+5-(后缀)规律:
- 运算数的相对顺序没变
- 运算符号相对顺序改变。优先级高的放前面。
以一个例子引入:a*(b+c)/d如何转化为后缀?
- 从左向右扫描, 分别存运算数和运算符号,
- 运算数先压入a,符号压入*,遇到括号,括号优先级更高,于是压入栈内
- 运算数压入b,符号压入+,加号优先级要高于括号,压入栈内
- 运算数压入c,符号压入右括号。
- 此时括号全部处理完毕,括号有关的都出栈,此时出栈为:)b+c(,得到b+c的值。
- 后面还有除号,优先级也比较高,但是相同优先级运算顺序是从左往右,此时栈内都出栈:得(b+c)*a
- 运算数压入d,符号压入/,运算,得((b+c)*a)/d
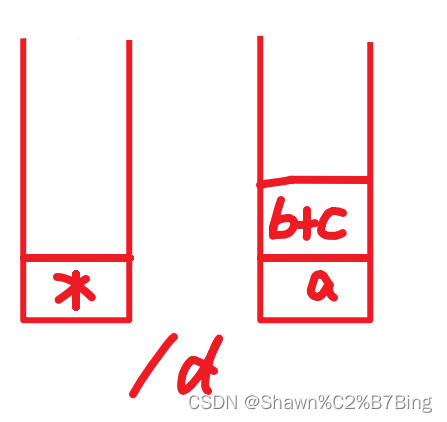
入栈顺序写出来即可得到后缀表达式:abc+*d/
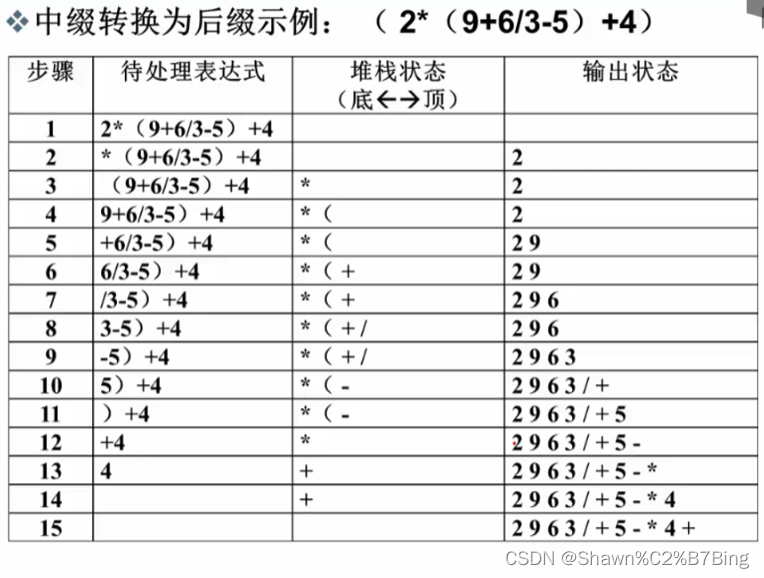
中缀表达式如何转换为后缀表达式

其他用途
- 函数调用和递归实现(函数栈)
- 深度优先搜索
- 回溯算法
- ...