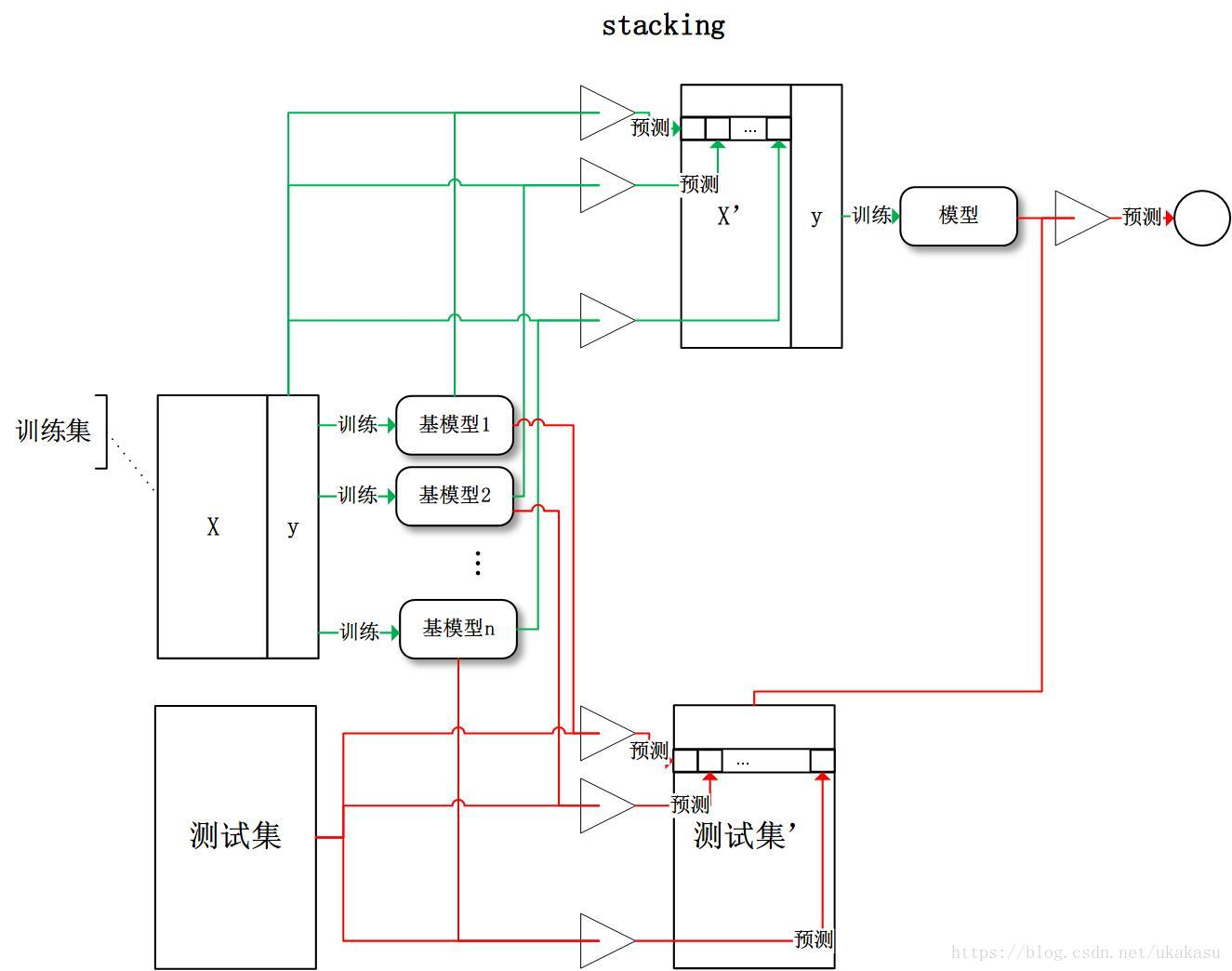
第一问

见 2023 年 五一杯 B 题过程 + 代码（第一问）

第二问

第二问考虑是一个时序预测问题，采用 ARIMA 模型即可

数据时序分析

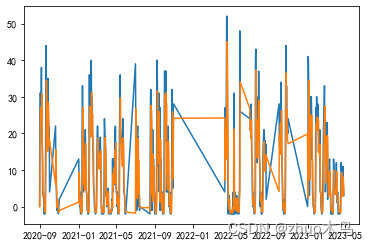
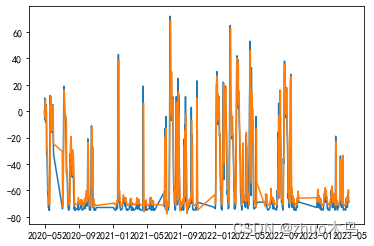
对于 每一个路径，快递数时间序列，以路径 G->L 为例，其取值如下所示：

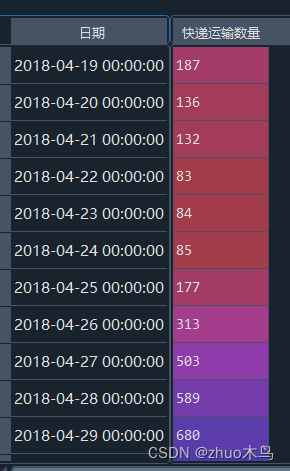
根据 ADF 检验，分析出路径 G->L 是否为稳定序列。根据 ADF 假设检验结果，由于ADF检验的 p值为： 0.002 检验统计量 ADF 为： -3.87。由于 p 值小于置信水平 0.05，因此可以认为时间序列是平稳的。

因此，采用 ARIMA(p,d,q)模型时，差分系数应为 d = 0。如果 ADF 检验的 p 值小于 0.05，则说明差分后的序列是平稳的。否则需要继续进行差分。此时差分系数 d 等于差分直至时序数据平稳时的差分次数。

绘制时序数据的自相关图，和偏自相关图，如下：


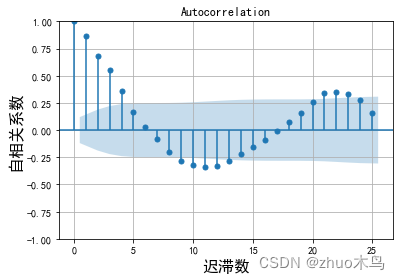
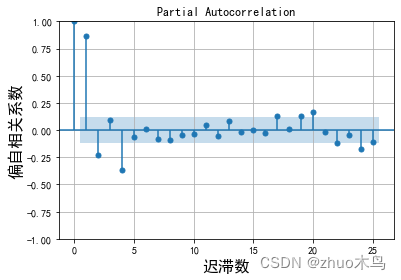
从图中可以得出，ARIMA 模型的自回归系数为 p=5（自相关系数截尾），移动平均系数 q=1(偏相关系数均衡衰减，取较小值 q)。

Auto-ARIMA

通过偏自相关系数图、自相关系数图筛选 p，q 带有主观性。因此结合 AIC 评价指标，将数据分为测试集和验证集，从而在众多（p，q）参数的组合中，筛选出最佳的 p，q 并与 ADF 检验确定的 d 值，从而得出最佳的 ARIMA 模型。

具体流程为：

1. 对每一个路径，绘制偏自相关系数、自相关系数图，筛选 p，q 的最大取值 $p_{max},q_{max}$。如上例 G-> L 路径可取 $p_{max}=5,q_{max}=1$
2. 取 $p\in (0,1,\cdots ,p_{m}ax),q\in (0,1,\cdots ,q_{m}ax)$，与 d 组合。d 根据 ADF 检验得来，如上例 G->L 路径可取 d = 0，构建 ARIMA 模型，同时按照 7：3 的比例将数据集切分为训练集和测试集
3. 将模型在训练集中训练并计算 AIC 指标（AIC 只能在训练的过程中计算）
4. 重复 2 -3 步骤，指导遍历完所有 p、d、q 组合，输出 AIC 最小（即最佳）的 ARIMA 模型作为预测模型。并采用 MAPE，即平均绝对偏差的百分数，在测试集中评价模型
5. 采用该预测模型预测数据的效果。

第二问求解

就以题目中的 M->U 为例吧，绘制图像

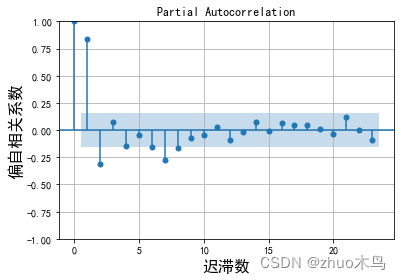
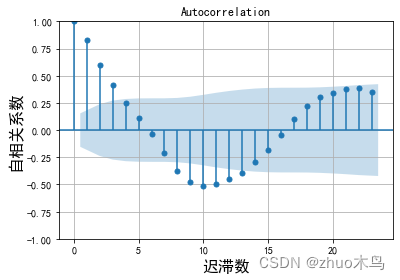
从自相关图和偏相关图可以取 $p_{max}=3,q_{max}=4$，根据 ADF 的结果：

差分0次后时序稳定
ADF检验的 p值为： 2.63e-08
检验统计量 ADF 为： -6.35

取 d = 0， $p_{max}=5,q_{max}=5$（考虑多种可能性）。根据网格寻优筛选出最佳模型为 p=1, d=0, q=3。

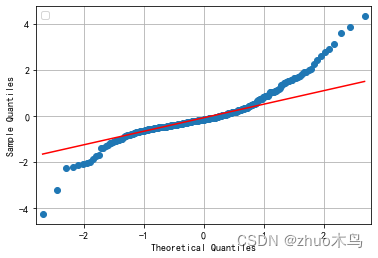
绘制出残差的 Q-Q 图，以观察残差是否服从正态分布：

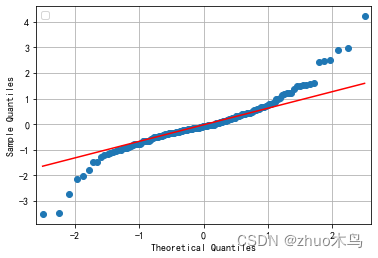
感觉还行，然后用 MAPE 数值分析他的拟合优度：
$$MAPE=\frac{100}{n}\sum _{i=1}^n\frac{|y_i-\widehat{y_i}|}{y_i}$$
其中，$n$ 是样本数量，$y_i$ 是实际值，$\widehat{y_i}$ 是预测值。可求出其值为：0.375

MAPE 的值越小，说明预测结果越准确。然而，MAPE 也有一些缺点，例如它对于实际值为 0 的样本会导致无法计算，同时它也对极端值比较敏感。因此，在使用 MAPE 作为评估指标时，需要结合实际情况进行分析。

解的情况

同理，可以求出其他模型，结论如下：

目前求解 M->U 路径
差分0次后时序稳定
ADF检验的 p值为： 0.0
检验统计量 ADF 为： -6.35
4 (根据自相关系数图像，筛选出的 p 值，下同）
3（根据偏自相关系数，筛选出的 q 值，下同）
模型的mape为： 0.38 最佳参数（p,d,q)为： (4, 0, 1)
M->U 路径中 4-18 和 4-19 的快递数量分别为：150.12 和 133.39
目前求解 Q->V 路径
差分1次后时序稳定
ADF检验的 p值为： 0.0
检验统计量 ADF 为： -8.39
8
4
模型的mape为： 46422190913933.88 最佳参数（p,d,q)为： (1, 1, 1)
Q->V 路径中 4-18 和 4-19 的快递数量分别为：48.17 和 48.17
目前求解 K->L 路径
差分0次后时序稳定
ADF检验的 p值为： 0.0
检验统计量 ADF 为： -4.4
5
3
模型的mape为： 0.26 最佳参数（p,d,q)为： (1, 0, 1)
K->L 路径中 4-18 和 4-19 的快递数量分别为：54.27 和 54.1
目前求解 G->V 路径
差分0次后时序稳定
ADF检验的 p值为： 0.0
检验统计量 ADF 为： -6.84
5
5
模型的mape为： 0.14 最佳参数（p,d,q)为： (1, 0, 1)
G->V 路径中 4-18 和 4-19 的快递数量分别为：599.71 和 552.6
目前求解 V->G 路径
差分0次后时序稳定
ADF检验的 p值为： 0.0
检验统计量 ADF 为： -6.94
5
2
模型的mape为： 0.1 最佳参数（p,d,q)为： (1, 0, 1)
V->G 路径中 4-18 和 4-19 的快递数量分别为：543.1800000000001 和 509.63
目前求解 A->Q 路径
差分0次后时序稳定
ADF检验的 p值为： 0.0
检验统计量 ADF 为： -4.65
6
3
模型的mape为： 110116766402955.56 最佳参数（p,d,q)为： (5, 0, 1)
A->Q 路径中 4-18 和 4-19 的快递数量分别为：129.09 和 119.93
目前求解 D->A 路径
差分0次后时序稳定
ADF检验的 p值为： 0.0
检验统计量 ADF 为： -5.45
4
2
模型的mape为： 1141794030037002.0 最佳参数（p,d,q)为： (1, 0, 1)
D->A 路径中 4-18 和 4-19 的快递数量分别为：43.18 和 42.47
目前求解 L->K 路径
差分0次后时序稳定
ADF检验的 p值为： 0.0
检验统计量 ADF 为： -4.16
6
2
模型的mape为： 0.15 最佳参数（p,d,q)为： (1, 0, 1)
L->K 路径中 4-18 和 4-19 的快递数量分别为：272.32 和 248.46

PS： ARIMA 效果其实也就那样，不过用 LSTM 更惨！！！，本人综合考虑了很多，最终决定采用 ARIMA 模型

D-> A，A-> Q, Q-> V, 这三个路径的 ARIMA 模型，MAPE 值太大了，预测结果不可信。应考虑采用其他办法。

我们可以画出他实际值和预测值的图像

A->Q:

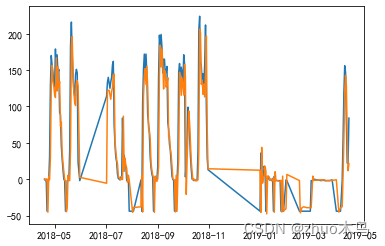
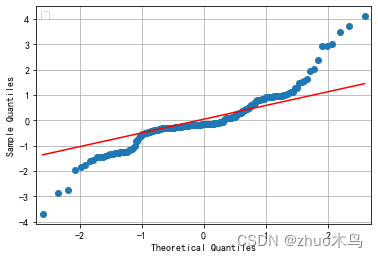
D-> A

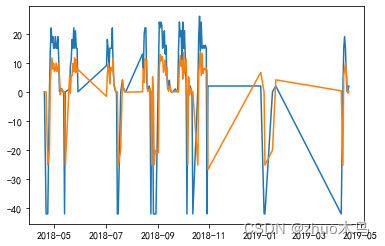
Q-V

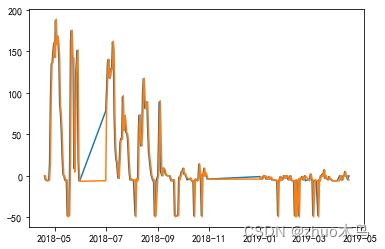
其实从图中可以看出，勉强可以用。把上述的解取整，就可以了。

总快递数

对总快递数也是一样的

差分0次后时序稳定，ADF检验的 p值为： 0.01 ，检验统计量 ADF 为： -3.56


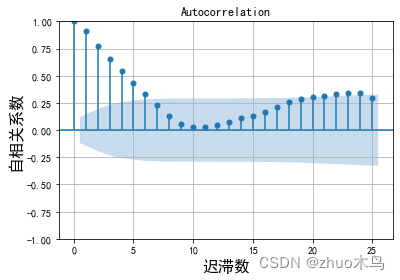
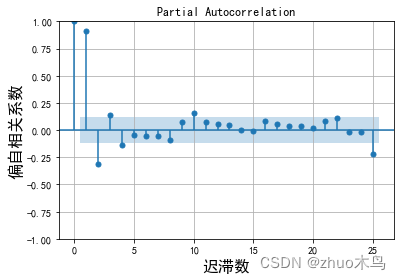
根据图片，设置 $p_{max}=7,q_{max}=5$，筛选模型，从而得到最佳模型的mape为： 1.45。 最佳参数（p,d,q)为： (1, 0, 2)

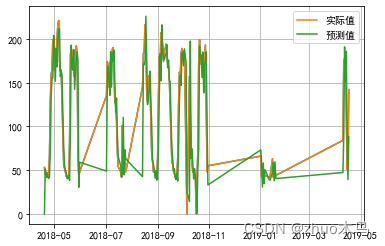
模型训练过程中的实际值和预测值如下，可以看到基本上是挺准确的。


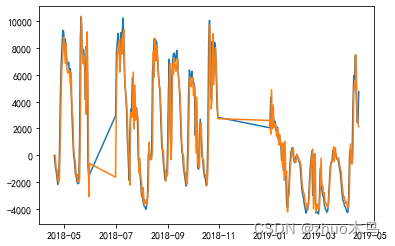
采用模型，求取4-18 和 4-19 的总快递数量分别为：10257.52 和 9473.54，然后取整就行了！

问题二解决。

第三问

首先对每一个路径数据增加一个标签列“可否正常发货”，取值为 0 和 1。1代表可以发货。若有某天缺失了数据，或该天的销售量为 0，则该行的 “可否正常发货” 为 0。

以 A->O 为例：

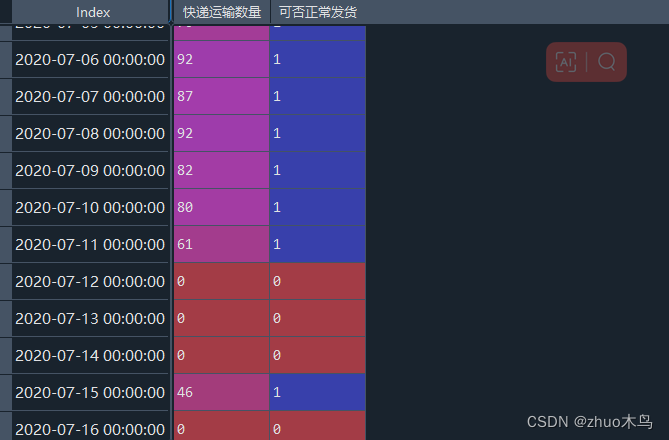
按照问题 2 的方法，对每一路径，按照“可否正常发货”这个时序数据，构建一个 ARIMA 模型。求解如下：

目前求取的路径是： I->S
差分0次后时序稳定
ADF检验的 p值为： 0.0
检验统计量 ADF 为： -4.18
模型的最佳参数（p，d，q）为： (3, 0, 1)
ARIMA 模型的精确度为: 0.94
I->S 路径中 4-18 和 4-19 的快递数量分别为：1 和 1
目前求取的路径是： M->G
差分0次后时序稳定
ADF检验的 p值为： 0.0
检验统计量 ADF 为： -9.79
模型的最佳参数（p，d，q）为： (1, 0, 1)
ARIMA 模型的精确度为: 0.84
M->G 路径中 4-18 和 4-19 的快递数量分别为：1 和 1
目前求取的路径是： S->Q
差分0次后时序稳定
ADF检验的 p值为： 0.0
检验统计量 ADF 为： -4.07
模型的最佳参数（p，d，q）为： (1, 0, 1)
ARIMA 模型的精确度为: 0.71
S->Q 路径中 4-18 和 4-19 的快递数量分别为：0 和 0
目前求取的路径是： V->A
差分0次后时序稳定
ADF检验的 p值为： 0.0
检验统计量 ADF 为： -4.29
模型的最佳参数（p，d，q）为： (2, 0, 2)
ARIMA 模型的精确度为: 0.88
V->A 路径中 4-18 和 4-19 的快递数量分别为：1 和 1
目前求取的路径是： Y->L
差分0次后时序稳定
ADF检验的 p值为： 0.0
检验统计量 ADF 为： -6.47
模型的最佳参数（p，d，q）为： (1, 0, 1)
ARIMA 模型的精确度为: 0.75
Y->L 路径中 4-18 和 4-19 的快递数量分别为：1 和 1
目前求取的路径是： D->R
差分0次后时序稳定
ADF检验的 p值为： 0.04
检验统计量 ADF 为： -2.99
模型的最佳参数（p，d，q）为： (2, 0, 1)
ARIMA 模型的精确度为: 0.84
D->R 路径中 4-18 和 4-19 的快递数量分别为：1 和 1
目前求取的路径是： J->K
差分0次后时序稳定
ADF检验的 p值为： 0.0
检验统计量 ADF 为： -4.27
模型的最佳参数（p，d，q）为： (1, 0, 2)
ARIMA 模型的精确度为: 0.83
J->K 路径中 4-18 和 4-19 的快递数量分别为：1 和 1
目前求取的路径是： Q->O
差分1次后时序稳定
ADF检验的 p值为： 0.0
检验统计量 ADF 为： -12.1
模型的最佳参数（p，d，q）为： (2, 1, 1)
ARIMA 模型的精确度为: 0.87
Q->O 路径中 4-18 和 4-19 的快递数量分别为：1 和 1
目前求取的路径是： U->O
差分0次后时序稳定
ADF检验的 p值为： 0.03
检验统计量 ADF 为： -3.11
模型的最佳参数（p，d，q）为： (1, 0, 2)
ARIMA 模型的精确度为: 0.86
U->O 路径中 4-18 和 4-19 的快递数量分别为：1 和 1
目前求取的路径是： Y->W
差分0次后时序稳定
ADF检验的 p值为： 0.0
检验统计量 ADF 为： -6.76
模型的最佳参数（p，d，q）为： (1, 0, 1)
ARIMA 模型的精确度为: 0.82
Y->W 路径中 4-18 和 4-19 的快递数量分别为：1 和 1

因此，对于 [‘I->S’, ‘M->G’, ‘V->A’, ‘Y->L’, ‘D->R’, ‘J->K’, ‘Q->O’, ‘U->O’, ‘Y->W’]，还要继续分析。这次亦可以用问题二的方法求解。不考虑不能发货的情况，直接拟合。（当然也可以考虑进去，看那种效果好咯）

目前求解 I->S 路径
差分0次后时序稳定
ADF检验的 p值为： 0.0
检验统计量 ADF 为： -8.31
根据图像，p_max 取值为5
根据图像，q_max 取值为4
I->S 路径中 4-18 和 4-19 的快递数量分别为：46.62 和 46.23
模型的预测拟合如下：

同理…

目前求解 V->A 路径
差分0次后时序稳定
ADF检验的 p值为： 0.04
检验统计量 ADF 为： -2.97
根据图像，p_max 取值为9
根据图像，q_max 取值为2
V->A 路径中 4-18 和 4-19 的快递数量分别为：51.8 和 54.17

后面不再列举

第四问

以 2023年4月23日 为例，首先求出“发货-收货”站点城市（共81个）对之间使用的路径，以 ‘R->O’ 为例，有：

[[‘R’, ‘K’, ‘V’, ‘F’, ‘O’],
[‘R’, ‘K’, ‘J’, ‘X’, ‘O’],
[‘R’, ‘X’, ‘O’],
[‘R’, ‘X’, ‘I’, ‘M’, ‘O’],
[‘R’, ‘F’, ‘U’, ‘G’, ‘O’],
[‘R’, ‘F’, ‘O’]]

求出这样的 81 各矩阵，然后问题转变为，从这个 81 个矩阵 $P_i,i\in (1,2,\cdots ,81)$，每个矩阵 $P_i$ 的 $n_i$ 个行向量构成的 $n_1\cdot n_2\cdot ,\cdots ,\cdot n_{81}=N$ 个组合中，找到其中一个组合，使得成本最小。

最简单的办法无疑是暴力求解，但是这不可取，假设每一个“发货-收货”站点城市使用的路径平均为 5 条，则$5^{81}=413590306276513837435704346034981426782906055450439453125$ 不可能求解得完。因此，可以考虑采用遗传算法求解。

遗传算法求解

设置基因型为一个长度为 81 的向量。向量中的每一个元素代表着 $P_i$ 选择的路径。以$P_{R->O}$为例，若该元素为 2，则表示路径 [‘R’, ‘K’, ‘J’, ‘X’, ‘O’] 。

基因的进化方式，考虑两种。一种是自进化，一种是交配。考虑产生 320 个基因型，构成 320 个个体组成的群落。将这个群落按照 8 个个体分成 40 个种群。每个种群中，挑选出最佳的 个体和次佳个体，得到 80 个个体。成本最低，则为最佳个体。

随后，保留最佳个体，然后又最佳个体随机改变其中{1,1，2,2，3,}基因，产生 5 个新的个体。再有最佳个体和次佳个体，交换基因片段产生新的 2 个个体，总共 1 + 5 + 2 = 8 个新个体进入下一代。

如是循环 200 遍，从迭代历史中，找出这 200 代，200 个群落中最佳的个体，即可成为最佳的路径设计和最低成本。

其中，自进化的方式能够加快算法的收敛，而交配的方式则提高了算法的随机性，使得不容易进入局部最优值。同时，分组的方式也能够避开局部最优的问题。

以 2023年4月23日 为例，使用遗传算法求解的最低成本的过程，如下所示。可以看出到 100 步开始就已经收敛了。

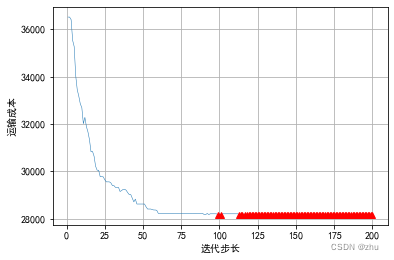
最终可得，最低的成本为 28170。

PS：有一些“发货-收货”站点城市对之间使用的路径，不会小于 5（可能是出题人出错了），所以这里用最小的路径去代替。

第五问

解决两个问题：

1. 时序数据季节性规律挖掘
2. 误差分布估计

SARIMA 模型拟合季节性规律

SARIMA（Seasonal Autoregressive Integrated Moving Average）模型是一种基于时间序列的预测模型，它是对ARIMA模型的一种扩展，用于处理季节性时间序列数据。SARIMA模型主要通过对时间序列数据进行差分、自回归、移动平均等处理，来描述和预测时间序列的变化趋势和季节性变化。

SARIMA模型的一般形式为SARIMA(p,d,q)(P,D,Q)s，其中：

• p：自回归项数（AR），表示当前时间点的值与前p个时间点的值之间的关系；
• d：差分阶数（I），表示对数据进行d阶差分后得到的时间序列是平稳的；
• q：移动平均项数（MA），表示当前时间点的值与前q个时间点的误差之间的关系；
• P：季节性自回归项数（SAR），表示当前时间点的值与前Ps个时间点的值之间的关系；
• D：季节性差分阶数（SI），表示对数据进行D阶差分后得到的时间序列是平稳的；
• Q：季节性移动平均项数（SMA），表示当前时间点的值与前Qs个时间点的误差之间的关系；
• s：季节周期，表示数据的季节性周期长度，比如一年有12个月，s=12。

SARIMA模型的预测公式如下：

$${\hat{y}}_{t+h|t}=\mu +\sum _{i=1}^p{\phi }_i(y_{t-i+h}-\mu )+\sum _{i=1}^P{\phi }_i(y_{t-is-h}-\mu )+\sum _{i=1}^q{\theta }_i{\epsilon }_{t-i+h}+\sum _{i=1}^Q{\theta }_i{\epsilon }_{t-is-h}$$

其中，${\hat{y}}_{t+h|t}$ 表示在时间 $t$ 时刻预测 $h$ 个时间点后的值，$\mu$ 表示时间序列的均值，${\phi }_i$ 表示自回归系数，${\theta }_i$ 表示移动平均系数，${\epsilon }_t$ 表示误差项，$y_t$ 表示在时间 $t$ 时刻的原始值。

SARIMA模型的训练过程中，需要确定模型的参数 $p,d,q,P,D,Q$ 和季节周期 $s$。一般可以通过观察时间序列的自相关图（ACF）和偏自相关图（PACF）来初步确定参数，然后使用最大似然估计（MLE）或贝叶斯信息准则（BIC）等方法来确定最优参数组合。最后，使用确定的模型对时间序列进行预测。