1.方差和协方差的定义

2.协方差矩阵

3. 协方差矩阵的应用

3.1 对两个类内协方差矩阵进行对角化

对两个类内协方差矩阵进行对角化，可以将它们变换为对角矩阵。这个过程可以通过对每个协方差矩阵进行特征值分解来实现，从而得到它们的特征向量和特征值，进而得到它们的对角矩阵形式。

这个过程的意义在于，它可以帮助我们找到一个新的坐标系，使得在这个坐标系下，每个特征之间都是独立的，从而简化了计算。具体来说，当我们使用对角协方差矩阵作为特征向量的坐标系时，它意味着每个特征之间都是相互独立的，从而方便了进一步的分析和处理。

在实际应用中，对角化协方差矩阵可以用于降维、特征选择和分类等任务。例如，在主成分分析（PCA）中，我们通常对类内协方差矩阵进行对角化，从而得到新的主成分，进而进行数据的降维和特征选择。在线性判别分析（LDA）中，对两个类内协方差矩阵进行对角化，可以得到判别变量，从而进行分类。

3.2 机器学习中的协方差矩阵应用小结

协方差矩阵是一个在机器学习中广泛使用的概念，主要用于描述数据集中不同特征之间的关系。以下是协方差矩阵在机器学习中的应用：

特征选择：协方差矩阵可以用来计算不同特征之间的相关性，如果某些特征高度相关，则可以选择其中一个特征进行训练，以避免过度拟合。
数据预处理：在进行数据预处理时，可以使用协方差矩阵来检测和移除数据中的共线性。共线性可能会导致训练过程中的不稳定性和精度下降。
主成分分析（PCA）：PCA是一种常用的数据降维技术，它使用协方差矩阵来确定数据集中的主成分。主成分通常是具有最大方差的特征，可以用于降低数据的维度。
线性回归：在线性回归中，协方差矩阵可以用来计算回归系数和截距项的最优解。这可以通过将数据集的协方差矩阵与目标向量的内积相除来完成。
高斯分布：在高斯混合模型中，协方差矩阵用于描述不同高斯分布之间的差异。它可以帮助确定哪些高斯分布最适合描述数据集。

总之，协方差矩阵在机器学习中具有广泛的应用，可以帮助我们更好地理解数据集并优化训练过程。

4. 协方差矩阵中心对齐

协方差矩阵中心对齐是一种在机器学习和数据分析中用于比较和对齐数据集的技术。协方差矩阵是用于描述两个或多个变量之间的统计关系的矩阵。它们通常用于分析多元数据，并识别数据集中的模式和趋势。协方差矩阵的中心是矩阵的中心点，表示矩阵中所有数据点的平均值。

在协方差矩阵中心对齐中，两个或多个协方差矩阵的中心点被对齐，以比较数据集中变量之间的模式和关系。这种对齐可以帮助识别数据集之间的相似之处和差异，并可用于将类似的数据点聚集在一起。

协方差矩阵中心对齐的数学原理是将多个协方差矩阵的中心点进行对齐，使它们在某种意义下具有相同的特征，以便比较它们之间的差异和相似性。下面是协方差矩阵中心对齐的详细数学原理：

假设有 n 个 d 维数据点，它们组成的数据集可以表示为矩阵 X，其中每行代表一个数据点。我们可以用以下公式计算数据集的协方差矩阵 C：

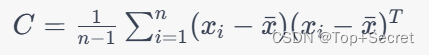
其中， $\bar{x}$ 是数据集的平均值向量，定义为：

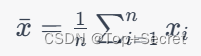
假设我们有 m 个数据集，每个数据集都有一个对应的协方差矩阵 $C_j$ ，其中 $j=1,2,...,m$ 。我们想要比较这些数据集之间的相似性和差异性。

首先，我们计算每个数据集的协方差矩阵的中心点，也就是平均值矩阵 $M_j$ ，定义为：

其中， $c_{ij}$ 表示协方差矩阵 $C_j$ 的第 i 行、第 j 列元素。

接下来，我们将平均值矩阵 $M_j$ 转换为向量 $m_j$ ，并将这些向量对齐。假设我们选择第一个数据集的平均值向量 $m_1$ 作为基准向量，则对于每个数据集 $j \neq 1$ ，我们可以计算出一个旋转矩阵 $R_j$ ，使得 $m_j$ 旋转后与 $m_1$ 对齐。旋转矩阵 $R_j$ 可以通过奇异值分解（SVD）等方法求解。