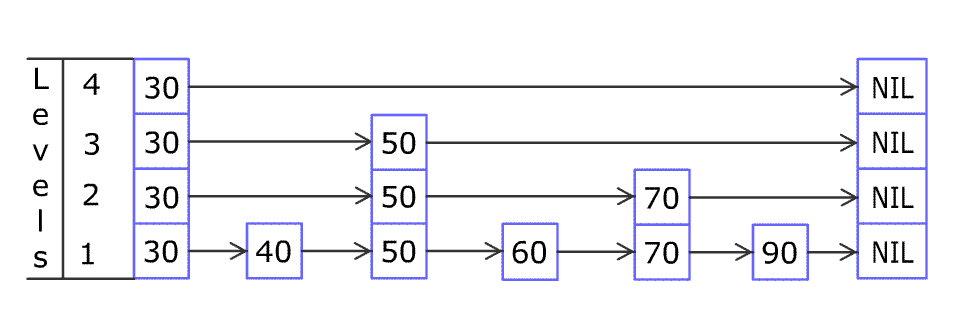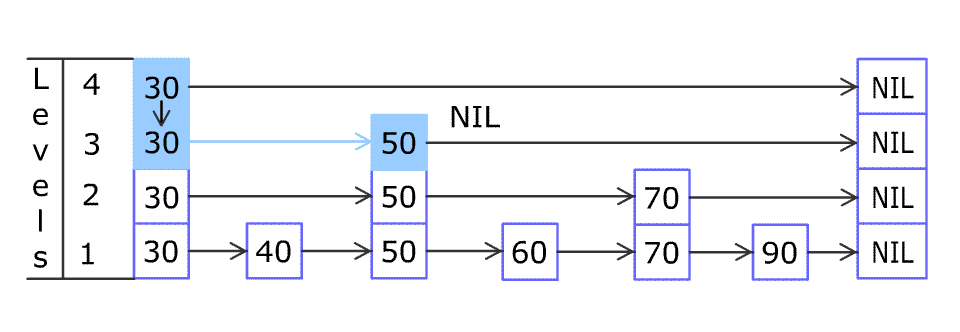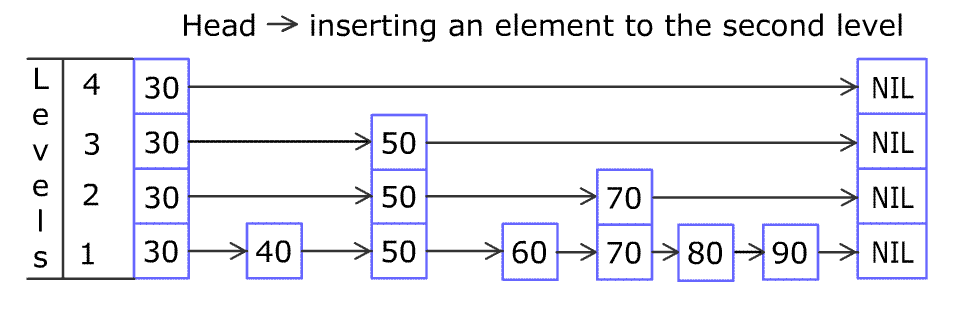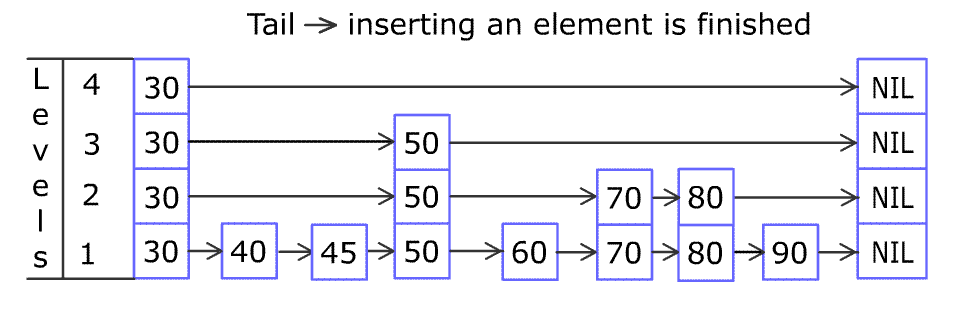
背包问题

有n个数对(a[i], b[i])，现在要求去除若干个数对使得$sum(a[i])/sum(b[i])=k$，你需要最大化sum(a[i])，其中 $n\le 100,k\le 10,a[i]\le 100$

比如下面的输入表示输入3(n的值)个数对，$sum(a[i])/sum(b[i])=2=k$，a[1]~a[3]为10 8 1，b[1]~b[3]为2 7 1

3 2
10 8 1
2 7 1

输出为

18

因为$(a[1]+a[2])/(b[1]+b[2])=(10+8)/(2+7)=2=k$，$sum(a[i])=10+8=18$

再如下面的输入：

5 3 // 一共5对数，sum(a[i]) / sum(b[i]) = 3
4 4 4 4 4
2 2 2 2 2

输出为：

-1

因为上面的$sum(a[i])/sum(b[i])$显然只能为2，不可能出现3

题目转换

观察$sum(a[i])/sum(b[i])=k$，移项可得$sum(a[i])=sum(b[i])\ast k$，再移项可得$sum(a[i])-sum(b[i])\ast k=0$，合并下可以得到$sum(a[i]-k\ast b[i])=0$

至此，问题也就转换成了第i个物体的体积是$v[i]=a[i]-k\ast b[i]$，价值是a[i]，的背包问题，为了防止总的体积被v[i]减成负的(j-v[i]要大于0)，所以初始化时j要足够大，我们取10000，这样我们就可以分成正负两个f来做了

本问题即是求1~i对应的a和b放入后${\sum }_{i=1}^{i}v[i]$是0，且$sum(a[i])={\sum }_{i=1}^{i}a[i]$即放入的所有的物体i的价值和最大)

java实现如下

import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner s = new Scanner(System.in);
        int n = s.nextInt();
        int k = s.nextInt();
        int[] a = new int[n + 1];
        int[] b = new int[n + 1];
        int[] v = new int[n + 1];
        for (int i = 1; i <= n; i++) a[i] = s.nextInt();
        for (int i = 1; i <= n; i++) b[i] = s.nextInt();
        int N = 10000, INF = 0x3f3f3f3f; // 这里的无穷大不要用系统自带的Integer.MIN_VALUE
        int[] f1 = new int[N + 1];
        int[] f2 = new int[N + 1];
        Arrays.fill(f1, -INF);
        Arrays.fill(f2, -INF);
        f1[0] = 0;
        f2[0] = 0;
        int[] c = new int[n + 1];
        for (int i = 1; i <= n; i++) {
            v[i] = a[i] - k * b[i];
            if (v[i] >= 0) {
                // j初始化10000因为要保证 j≥v[i]的条件不成立前i要能循环完，因此j要足够大
                for (int j = N; j >= v[i]; j--) f1[j] = Math.max(f1[j], f1[j - v[i]] + a[i]); // 正体积时的背包
            } else {
                // 处理v[i]小于0的情况
                v[i] = -v[i];
                for (int j = N; j >= v[i]; j--) f2[j] = Math.max(f2[j], f2[j - v[i]] + a[i]); // 负体积时的背包
            }
        }
        int res = -1;
        for (int i = 0; i <= N; i++) {
            res = Math.max(res, f1[i] + f2[i]);
        }
        System.out.println(res == 0 ? -1 : res); // 和为0表示没有满足条件的背包
    }
}

题目分析

是个典型的01背包问题，这里的花费不是体积，而是时间。用f[i]表示到i时刻最大能救多少价值，j表示第j个物品救还是不救

$f[i]=max(f[i],f[i-t[j]]+p[j])$ 其中 $(i-t[j])\le d[j]$否则第j个物品就开始燃烧而没法抢救了

因此先对物品按照d[i]进行排序，然后依次更新，即按照燃烧开始的时刻早晚依次开始抢救

代码如下：参考地 https://www.luogu.com.cn/blog/213870/solution-cf864e

这道题很明显是一个01背包。

第一问：先将所有数据存在结构体里，按 d[i] 排序，然后当成普通01背包做，在第二层循环时边界调整为 d[i] 即可。

转移方程： $f[i]=max(f[i],f[i-t[i]]+p[i])$

对于第二问，每一个 f[i] 都有一个对应的数组储存最优解下取的物品。

注意：第 i 件物品在 d[i] 秒彻底焚毁，所以第二层循环只能循环到 $d[i]-1$ 。

代码：

#include<bits/stdc++.h>

using namespace std;
struct Item { //结构体，p,t,d作用于题面里相同，num储存编号
    int p, t, d, num;
} a[110];
int n, f[2010], ans, ansnum; //ans储存最大价值，ansnum储存最大价值对应的f[i]的编号
vector<int> v[2010]; // 列表数组，v[i]表示f[i]时刻抢到的东西的列表

bool cmp(Item i1, Item i2) {
    return i1.d < i2.d; //按d排序
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> a[i].t >> a[i].d >> a[i].p;
        a[i].num = i;
    }
    sort(a + 1, a + n + 1, cmp);
    for (int i = 1; i <= n; i++)
        for (int j = a[i].d - 1; j >= a[i].t; j--) // 只能取一次，倒序循环（从a[i].d-1开始！）
            if (f[j - a[i].t] + a[i].p > f[j]) {
                f[j] = f[j - a[i].t] + a[i].p; // 转移方程
                v[j] = v[j - a[i].t]; // 把上一个抢东西的时刻抢到的东西列表复制过来(注意是深度拷贝)
                v[j].push_back(a[i].num); // 更新v[j]，把本轮新抢的东西加入进去
            }
    for (int i = 0; i <= 2000; i++) { // 循环获取抢救到最大价值的时刻
        if (f[i] > ans) {
            ans = f[i];
            ansnum = i;
        }
    }
    cout << ans << endl << v[ansnum].size() << endl;
    for (int i : v[ansnum]) cout << i << " "; // 打印获取的最大价值时的抢到了哪些物品
    return 0;
}

Java实现如下：C++的vector和Java的List使用时有很大差异的，前者赋值会自动拷贝，后者赋值时引用赋值

import java.util.*;

public class Main {
    static class Item implements Comparable<Item> {
        int p, t, d, num;

        // 构造函数的参数顺序务必正确
        public Item(int t, int d, int p, int num) {
            this.t = t;
            this.d = d;
            this.p = p;
            this.num = num;
        }

        @Override
        public int compareTo(Item o) {
            return d - o.d;
        }
    }

    static int n, ans, ansnum;
    static List<Integer>[] v = new List[2010]; // 列表数组，v[i]表示f[i]时刻抢到的东西的列表
    static int[] f = new int[2010]; // f[i]表示到i时刻最大能救多少价值， i在[0, 2000]，为了防止边界问题多取一点

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        Item[] a = new Item[n + 1];
        for (int i = 1; i <= n; i++) a[i] = new Item(sc.nextInt(), sc.nextInt(), sc.nextInt(), i);
        Arrays.sort(a, 1, n + 1);
        for (int i = 0; i < v.length; i++) v[i] = new ArrayList<>();
        v[0].add(1);
        for (int i = 1; i <= n; i++) {
            for (int j = a[i].d - 1; j >= a[i].t; j--) { // 只能取一次，倒序循环（从a[i].d-1开始！）
                if (f[j - a[i].t] + a[i].p > f[j]) {
                    f[j] = f[j - a[i].t] + a[i].p; // 转移方程
                    v[j] = new ArrayList<>();
                    for (int e : v[j - a[i].t]) v[j].add(e); // 把上一个抢东西的时刻抢到的东西列表复制过来(注意是深度拷贝)
                    v[j].add(a[i].num); // 更新v[j]，把本轮新抢的东西加入进去
                }
            }
        }
        for (int i = 0; i <= 2000; i++) { // 循环获取抢救到最大价值的时刻
            if (f[i] > ans) {
                ans = f[i];
                ansnum = i;
            }
        }
        System.out.println(ans);
        System.out.println(v[ansnum].size() - 1);
        for (int i = 1; i < v[ansnum].size(); i++) System.out.print(v[ansnum].get(i) + " "); // 打印获取的最大价值时的抢到了哪些物品
    }
}

题意：有n种面额的硬币。面额、个数分别为v[i]、c[i]，求最多能搭配出几种不超过m的金额？

思路：f[i][j]就是总数为j的价值金额是否已经有了含有面额i的硬币可以满足这种搭配方法，如果现在没有，那么我们就一个个硬币去尝试直到有，这种价值方法有了的话，那么就是总方法数加1。

显然是个多重背包可行性问题，背包的体积V在这里是m，每个背包的体积是v[i]，每个背包的使用个数最多是c[i]个，直接套用多重背包的代码模板很好解决这个问题，简化成f[j]即可

#include <cstdio>
#include <cstring>

using namespace std;

int f[100005]; //表示当前i价格是否出现过，1表示出现出，0表示没有可以拼接的方案
int sum[100005];//当价格达到i时，最多使用这一种硬币的次数
int v[105], c[105];

int main() {
    int i, j, n, m;
    while (~scanf("%d%d", &n, &m), n + m) {
        for (i = 1; i <= n; i++) scanf("%d", &v[i]);
        for (i = 1; i <= n; i++) scanf("%d", &c[i]);
        memset(f, 0, sizeof(f));
        f[0] = 1;
        int ans = 0;
        for (i = 1; i <= n; i++) { // i表示硬币的面额
            memset(sum, 0, sizeof(sum));// 关键是用sum来限定了次数，sum[i]表示为了拼出金额j用了几个面额i
            for (j = v[i]; j <= m; j++) { // 多重背包从小到大更新
                if (!f[j] && f[j - v[i]] && sum[j - v[i]] < c[i]) { // 如果j价格没有出现过，且j-v[i]出现过，并且使用i硬币的次数没有超出给定的数量
                    f[j] = 1; // 1表示j这种金额可以拼出来了
                    sum[j] = sum[j - v[i]] + 1;// 使用次数+1
                    ans++; // 小于金额m的所有的拼的方案都要累计
                }
            }
        }
        printf("%d\n", ans);
    }
    return 0;
}

Java实现如下，注意一开始按照用例的上限固定好数组的大小要比根据数据动态分配省内存，否则容易超出程序的内存限制

// 单调队列，单调栈和单调队列的理解见博客：https://blog.csdn.net/shxifs/article/details/101058167

import java.io.*;
import java.util.*;

public class Main {
    static int[] f = new int[100005]; // f[j]表示当前j价金额是否出现过，1表示出现出，0表示没有可以拼接的方案
    static int[] sum = new int[100005]; // sum[j]表示当金额为j时时，最多使用第i种硬币的次数
    static int[] v = new int[105]; // v[i]表示硬币i的面额
    static int[] c = new int[105]; // c[i]表示硬币i的个数

    public static void main(String[] args) throws IOException {
        Scanner sc = new Scanner(System.in);
        while (sc.hasNext()) {
            int n = sc.nextInt(), m = sc.nextInt();
            if(n == 0 && m == 0) return;
            Arrays.fill(f, 0);
            for (int i = 1; i <= n; i++) v[i] = sc.nextInt();
            for (int i = 1; i <= n; i++) c[i] = sc.nextInt();
            f[0] = 1; // 面额为0不用拼接，肯定可以
            int ans = 0;
            for (int i = 1; i <= n; i++) { // i表示硬币的面额
                Arrays.fill(sum, 0);
                for (int j = v[i]; j <= m; j++) { // 多重背包从小到大更新
                    if (f[j] == 0 && f[j - v[i]] == 1 && sum[j - v[i]] < c[i]) { // 如果j价格没有出现过，且j-v[i]出现过，并且使用i硬币的次数没有超出给定的数量
                        f[j] = 1; // 1表示j这种金额可以拼出来了
                        sum[j] = sum[j - v[i]] + 1;// 使用次数+1
                        ans++; // 小于金额m的所有的拼的方案都要累计
                    }
                }
            }
            System.out.println(ans);
        }
    }
}

题解：https://www.luogu.com.cn/problem/solution/CF755F

如何最小化收不到礼物的人数？

• 对于一个偶环，假设长度为k，那么只要有k/2个人忘带礼物，k个人就全都收不到礼物
• 对于一个奇环，假设长度为k，那么需要有(k + 1)/2个人忘带礼物，k个人就全都收不到礼物
  贪心即可

如何最小化收不到礼物的人数？

• 如果有一个大小为m的环，只要让这m个人都忘带，就只有m个人收不到礼物(这样一个人就只影响了一个人，比前面一个人影响两个人要好得多)。因此如果能找到若干个环，使得他们的长度之和刚好是k(这里可以看出来是个背包问题)，那么答案就是k
• 否则会有一个环不能被完全覆盖，还会再牵连一个人，答案就是k+1

现在问题变成了有m个环，第i个环的长度为L[i]，该长度的环一共有C[i]个，问能否凑出长度为k的方案。显然是多重背包问题！

用二进制分组，拆分成log(C[i])个物品，做01背包，时间复杂度为$O(nlogn)$

// 参考：https://www.luogu.com.cn/problem/solution/CF755F 第2个题解
#include<iostream>
#include<algorithm>
#include<cstdio>

using namespace std;

int a[1000005]; // a[i]表示图中i指向的下一个点(一个人的礼物要送给哪一个人)
int huan[1000005];  // huan[i]表示第i个环的长度(和下面的i进行区分，这里是个环不管长度是否相等都算一个i)
int shu[1000005]; // shu[i]表示第i个不同长度的环在多重背包中能用几次，即把相同长度的环进行计数。i表示第i个不同长度的环
int re[1000005]; // re[i]表示第i个不同长度的环的长度是多少
int opt[1000005]; // opt[i]表示01背包中第i个背包的容量，题目中表示第i个不同长度环二进制拆分后累计的个数
bool vis[1000005]; // DFS中记录被访问过地点，防止重复计算
bool dp[1000005]; // dp[i]表示i个人忘带礼物时，能否只影响i个人

/**
 * DFS获取环的长度(环内点的个数)
 * @param now 当前的人
 * @param from 根节点，即环遍历的起点
 * @param dep 环的长度(点的个数)
 */
int dfs(int now, int from, int dep) {
    if (now == from) return dep; // DFS回到起点说明环遍历完了，返回环的长度
    else {
        vis[now] = true;
        dfs(a[now], from, dep + 1); // DFS遍历下now的一个邻接点(即第now个人忘带礼物影响的另一个人)
    }
}

int main() {
    dp[0] = 1;
    int n, k;
    cin >> n >> k;
    for (int i = 1; i <= n; i++) scanf("%d", &a[i]);

    // 1.DFS获取每个环内点的个数
    int cnt = 0;
    for (int i = 1; i <= n; i++) {
        if (vis[i] == 0) huan[++cnt] = dfs(a[i], i, 1);
    }

    // 2.求最大值，即一个人尽量影响两个人  ------ 贪心，先按照环的长度从小到大排序
    sort(huan + 1, huan + cnt + 1);
    int maxans = 0; // 求最大值，初始化为最小值
    int left = k; // 剩下忘带的人
    int weipipei = 0; // 奇环上未匹配的人数
    for (int i = 1; i <= cnt; i++) { // 遍历所有的环
        // 尽可能先让一个人忘带影响两个人，这样才能最大化
        if (huan[i] / 2 <= left) { // 环的长度不够分配忘带的人
            left -= huan[i] / 2; // 当前的环分配环长度的一半的人
            maxans += huan[i] / 2 * 2; // 最大的分配不到的人就是环长度的最近偶数值
        } else {
            maxans += left * 2; // 剩余的未带的人正好能全部放进当前的环里，那么最大值加上2倍的剩余未匹配的人即可
            left = 0; // 剩下的忘带的人直接归零了，
            break; // 可以直接退出了，这一步是防止超时的关键，没有这一步肯定TLE
        }
        if (huan[i] & 1) weipipei++; // 奇数环处理：每个奇数环都会有一个人剩下无法被影响
    }
    maxans += min(left, weipipei); // 剩下的忘带的人(left)可以使用一个人抵消一个人的策略来处理未分配的人(weifenpei)，所以需要取二者的较小值

    // 3.求最小值，即一个人尽量影响一个人，多重背包，够分就表明能做到，否则就得+1
    int temp = 0;
    for (int i = 1; i <= cnt; i++) {
        if (huan[i] == huan[i - 1]) shu[temp]++; // 对相同长度的环进行计数，因为先按照环长度进行排序了，所以不断检查相邻的huan[i]是否相等即可
        else {
            shu[++temp]++; // 一旦环长度变了，就开始新一轮的计数
            re[temp] = huan[i]; // 初次需要把第i个不同长度的环的长度存下来
        }
    }

    // 3.1 多重背包的二进制优化
    cnt = 0;
    for (int i = 1; i <= temp; i++) {
        for (int j = 1; shu[i] >
                        0; j <<= 1) { // j <<= 1表示不断乘以2，比如1、2、4、8...都放到01背包的opt[cnt]中，直到shu[i]不够再分，shu[i]减去此时的j的结果放到opt[cnt]即可
            // leftt表示01背包问题中第cnt个物品的大小，这里是使用次数的二进制拆分
            int leftt = min(shu[i], j); // 看看二进制拆分还够不够分，够分就接着取不断扩大2倍的j，否则就取shu[i]减去前面的1+2+4+...后剩下的值
            opt[++cnt] = leftt * re[i]; // re[i]表示第i个不同长度环的长度，leftt表示二进制拆分后当前可以用几次，二者相乘才是背包的当前轮次消耗值
            shu[i] -= leftt;
        }
    }

    // 3.2 01背包问题解决，总的容量V在题目里为k，即一共忘带的人数；第i个要放入的物品的体积为opt[i]，即题目中第i个环二进制拆分后每个可以放入的总人数
    for (int i = 1; i <= cnt; i++) {
        for (int j = k; j >= opt[i]; j--) {
            if (dp[j - opt[i]]) dp[j] = true; // j - opt[i]的背包能拼出来，那么加上当前的opt[i]的物品肯定能占满容量为j的背包
        }
    }
    int minans = k; // 先默认全能拼出来，即k个人不带礼物只会影响到k个人(即这k个人都能正好分配到不同的环中)
    if (!dp[k])minans++; // 第k个人拼不出来，说明还要再多影响一个人，即要+ 1
    cout << minans << ' ' << maxans << endl;
}

Java实现如下：

// 单调队列，单调栈和单调队列的理解见博客：https://blog.csdn.net/shxifs/article/details/101058167
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;

public class Main {
    static final int N = 1000005;
    static int[] a = new int[N]; // a[i]表示图中i指向的下一个点(一个人的礼物要送给哪一个人)
    static int[] huan = new int[N];  // huan[i]表示第i个环的长度(和下面的i进行区分，这里是个环不管长度是否相等都算一个i)
    static int[] shu = new int[N]; // shu[i]表示第i个不同长度的环在多重背包中能用几次，即把相同长度的环进行计数。i表示第i个不同长度的环
    static int[] re = new int[N]; // re[i]表示第i个不同长度的环的长度是多少
    static int[] opt = new int[N]; // opt[i]表示01背包中第i个背包的容量，题目中表示第i个不同长度环二进制拆分后累计的个数
    static boolean[] vis = new boolean[N]; // DFS中记录被访问过地点，防止重复计算
    static boolean[] dp = new boolean[N]; // dp[i]表示i个人忘带礼物时，能否只影响i个人

    /**
     * DFS获取环的长度(环内点的个数)
     *
     * @param now  当前的人
     * @param from 根节点，即环遍历的起点
     * @param dep  环的长度(点的个数)
     */
    static int dfs(int now, int from, int dep) {
        if (now == from) return dep; // DFS回到起点说明环遍历完了，返回环的长度
        else {
            vis[now] = true;
            return dfs(a[now], from, dep + 1); // DFS遍历下now的一个邻接点(即第now个人忘带礼物影响的另一个人)
        }
    }

    public static void main(String[] args) throws IOException {
        BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
        String[] nk = bf.readLine().split(" ");
        int n = Integer.parseInt(nk[0]), k = Integer.parseInt(nk[1]);
        String[] chs = bf.readLine().trim().split(" ");
        for (int i = 1; i <= n; i++) a[i] = Integer.parseInt(chs[i - 1]);

        // 1.DFS获取每个环内点的个数
        int cnt = 0;
        for (int i = 1; i <= n; i++) {
            if (!vis[i]) huan[++cnt] = dfs(a[i], i, 1);
        }

        // 2.求最大值，即一个人尽量影响两个人  ------ 贪心，先按照环的长度从小到大排序
        Arrays.sort(huan, 1, cnt + 1);
        int maxans = 0; // 求最大值，初始化为最小值
        int left = k; // 剩下忘带的人
        int weipipei = 0; // 奇环上未匹配的人数
        for (int i = 1; i <= cnt; i++) { // 遍历所有的环
            // 尽可能先让一个人忘带影响两个人，这样才能最大化
            if (huan[i] / 2 <= left) { // 环的长度不够分配忘带的人
                left -= huan[i] / 2; // 当前的环分配环长度的一半的人
                maxans += huan[i] / 2 * 2; // 最大的分配不到的人就是环长度的最近偶数值
            } else {
                maxans += left * 2; // 剩余的未带的人正好能全部放进当前的环里，那么最大值加上2倍的剩余未匹配的人即可
                left = 0; // 剩下的忘带的人直接归零了，
                break; // 可以直接退出了，这一步是防止超时的关键，没有这一步肯定TLE
            }
            if ((huan[i] & 1) == 1) weipipei++; // 奇数环处理：每个奇数环都会有一个人剩下无法被影响
        }
        maxans += Math.min(left, weipipei); // 剩下的忘带的人(left)可以使用一个人抵消一个人的策略来处理未分配的人(weifenpei)，所以需要取二者的较小值

        // 3.求最小值，即一个人尽量影响一个人，多重背包，够分就表明能做到，否则就得+1
        int temp = 0;
        for (int i = 1; i <= cnt; i++) {
            if (huan[i] == huan[i - 1]) shu[temp]++; // 对相同长度的环进行计数，因为先按照环长度进行排序了，所以不断检查相邻的huan[i]是否相等即可
            else {
                shu[++temp]++; // 一旦环长度变了，就开始新一轮的计数
                re[temp] = huan[i]; // 初次需要把第i个不同长度的环的长度存下来
            }
        }

        // 3.1 多重背包的二进制优化
        cnt = 0;
        for (int i = 1; i <= temp; i++) {
            for (int j = 1; shu[i] >
                    0; j <<= 1) { // j <<= 1表示不断乘以2，比如1、2、4、8...都放到01背包的opt[cnt]中，直到shu[i]不够再分，shu[i]减去此时的j的结果放到opt[cnt]即可
                // leftt表示01背包问题中第cnt个物品的大小，这里是使用次数的二进制拆分
                int leftt = Math.min(shu[i], j); // 看看二进制拆分还够不够分，够分就接着取不断扩大2倍的j，否则就取shu[i]减去前面的1+2+4+...后剩下的值
                opt[++cnt] = leftt * re[i]; // re[i]表示第i个不同长度环的长度，leftt表示二进制拆分后当前可以用几次，二者相乘才是背包的当前轮次消耗值
                shu[i] -= leftt;
            }
        }

        // 3.2 01背包问题解决，总的容量V在题目里为k，即一共忘带的人数；第i个要放入的物品的体积为opt[i]，即题目中第i个环二进制拆分后每个可以放入的总人数
        dp[0] = true;
        for (int i = 1; i <= cnt; i++) {
            for (int j = k; j >= opt[i]; j--) {
                if (dp[j - opt[i]]) dp[j] = true; // j - opt[i]的背包能拼出来，那么加上当前的opt[i]的物品肯定能占满容量为j的背包
            }
        }
        int minans = k; // 先默认全能拼出来，即k个人不带礼物只会影响到k个人(即这k个人都能正好分配到不同的环中)
        if (!dp[k]) minans++; // 第k个人拼不出来，说明还要再多影响一个人，即要+ 1
        System.out.println(minans + " " + maxans);
    }
}

题解：https://www.luogu.com.cn/problem/solution/P1941 其中比较好的题解：https://www.luogu.com.cn/blog/YRwtm/post-2014noip-ti-gao-zu-d1t3-post

一个简单的思路：用f[i][j]表示第i列第j的高度所需要的最小点击次数。

枚举在第i-1列点k次屏幕，用$f[i-1][j-k\ast up[i-1]]+k$来更新$f[i][j]$，$k\ast up[i-1]$表示第i-1列点击k次。

也就是当成多重背包来做，这样的时间复杂度时$O(n{m}^2)$，只能得到70分，需要使用单调队列来优化，才能做到$O(nm)$

更简单的做法：可以把点屏幕当成完全背包来做：

• 先跳到下一个位置，用多重背包：$f[i][j]=min(f[i][j],f[i-1][j-up[i-1]]+1)$
• 到下一个未知了，假设可以跳无限次，就成了完全背包：$f[i][j]=min(f[i][j],f[i][j-up[i-1]]+1)$
  即先假设第i列没有管子，更新完所有的f[i][j]之后，把管子对应的部分的f[i][j]设置为INF即可，此时的时间复杂度为$O(nm)$

#include<bits/stdc++.h>

using namespace std;

struct Pipe {
    int pos, up, bottom;
} pipe[10010];

const int MAXN = (1 << 30);
int n, m, k, lift[10010], down[10010], f[10010][1010];

bool cmp(Pipe a, Pipe b) {
    return a.pos < b.pos;
}

int main() {
    scanf("%d%d%d", &n, &m, &k);
    for (int i = 0; i <= n - 1; i++) scanf("%d%d", &lift[i], &down[i]);
    for (int i = 1; i <= k; i++) scanf("%d%d%d", &pipe[i].pos, &pipe[i].bottom, &pipe[i].up);
    sort(pipe + 1, pipe + k + 1, cmp);
    for (int i = 0; i <= n; i++)
        for (int j = 0; j <= m; j++) f[i][j] = MAXN;
    for (int i = 1; i <= m; i++) f[0][i] = 0;
    int nump = 1;
    for (int i = 1; i <= n; i++) {
        int lower = 1, upper = m;
        if (pipe[nump].pos == i) {
            upper = pipe[nump].up - 1;
            lower = pipe[nump++].bottom + 1;
        }
        for (int j = 1; j <= upper; j++) { // 上升
            for (int k = j - lift[i - 1]; k <= m; k++) {
                if (k > j - lift[i - 1] && j < m) break; // 高度不是m就只做一次退出
                if (k >= 1) f[i][j] = min(f[i][j], min(f[i - 1][k], f[i][k]) + 1);
            }
        }
        for (int j = lower; j <= upper; j++) {
            if (j + down[i - 1] <= m) { // 下降
                f[i][j] = min(f[i][j], f[i - 1][j + down[i - 1]]);
            }
        }
        for (int j = 1; j <= lower - 1; j++) f[i][j] = MAXN; // 把柱子原来的最大值填回去
    }
    int minn = MAXN;
    bool flag = false;
    for (int i = n; i >= 1; i--) {
        for (int j = 1; j <= m; j++) {
            if (f[i][j] != MAXN) {
                flag = true;
                minn = min(minn, f[i][j]);
            }
        }
        if (flag) {
            if (i == n) {
                printf("1\n%d", minn);
                return 0;
            } else {
                for (int j = k; j >= 1; j--) {
                    if (i >= pipe[j].pos) {
                        printf("0\n%d", j);
                        return 0;
                    }
                }
            }
        }
    }
    printf("0\n0");
    return 0;
}