目录
- 概念
- 1. 基本思想
- 2. 实现逻辑
- 3. 复杂度分析
- 4、代码
概念
归并排序,是创建在归并操作上的一种有效的排序算法。算法是采用分治法(Divide and Conquer)的一个非常典型的应用,且各层分治递归可以同时进行。归并排序思路简单,速度仅次于快速排序,为稳定排序算法,一般用于对总体无序,但是各子项相对有序的数列。
1. 基本思想
归并排序是用分治思想,分治模式在每一层递归上有三个步骤:
● 分解(Divide):将n个元素分成个含n/2个元素的子序列。
● 解决(Conquer):用合并排序法对两个子序列递归的排序。
● 合并(Combine):合并两个已排序的子序列已得到排序结果。
2. 实现逻辑
递归法
① 申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列
② 设定两个指针,最初位置分别为两个已经排序序列的起始位置
③ 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
④ 重复步骤③直到某一指针到达序列尾
⑤ 将另一序列剩下的所有元素直接复制到合并序列尾
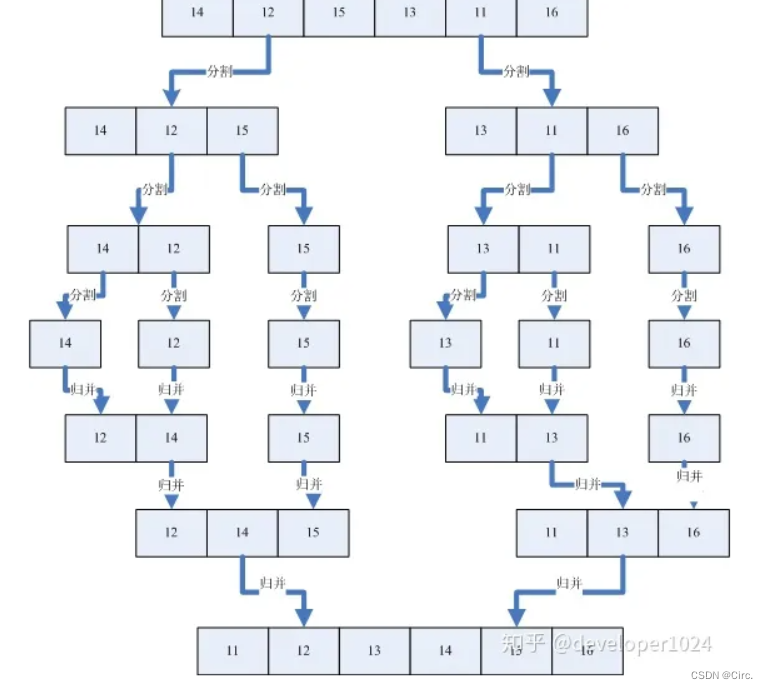
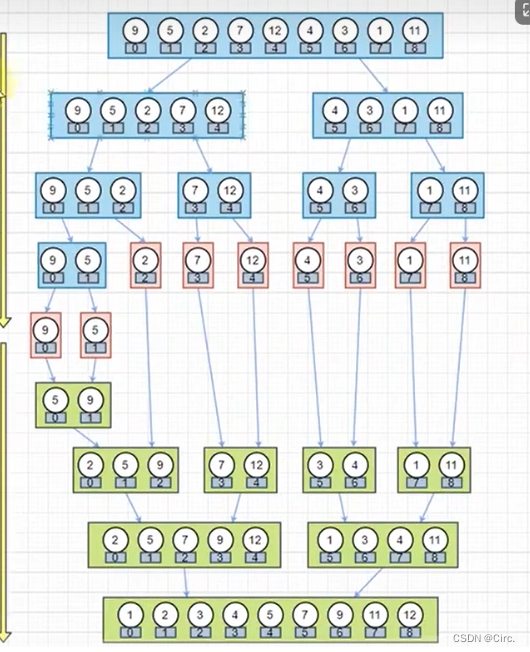
上图中首先把一个未排序的序列从中间分割成2部分,再把2部分分成4部分,依次分割下去,直到分割成一个一个的数据,再把这些数据两两归并到一起,使之有序,不停的归并,最后成为一个排好序的序列。
3. 复杂度分析
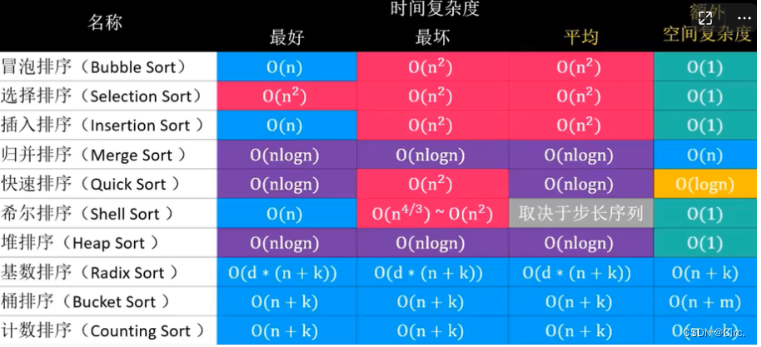
平均时间复杂度:O(nlogn)
最佳时间复杂度:O(nlogn)
最差时间复杂度:O(nlogn)
空间复杂度:O(n)
稳定性:稳定
不管元素在什么情况下都要做这些步骤,所以花销的时间是不变的,所以该算法的最优时间复杂度和最差时间复杂度及平均时间复杂度都是一样的为:O( nlogn )
归并的空间复杂度就是那个临时的数组和递归时压入栈的数据占用的空间:n + logn;所以空间复杂度为: O(n)。
归并排序算法中,归并最后到底都是相邻元素之间的比较交换,并不会发生相同元素的相对位置发生变化,故是稳定性算法。
4、代码
package Sort;
import java.util.Arrays;
/**
* @BelongsProject: JAVAtest
* @BelongsPackage: Sort
* @Author:
* @CreateTime: 2023-05-01 10:18
* @Description: TODO
* @Version: 1.0
*/
public class divideAndConquer {
public static void main(String[] args) {
// 定义待排序数组
int[] arr = {14,12,15,13,11,16};
//新建一个临时数组存放
int[] tmp = new int[arr.length];
// 归并排序
mergeSort(arr, 0, arr.length - 1, tmp);
for (int i = 0; i < arr.length; i++) {
// 归并排序
System.out.print(arr[i] + " ");
}
}
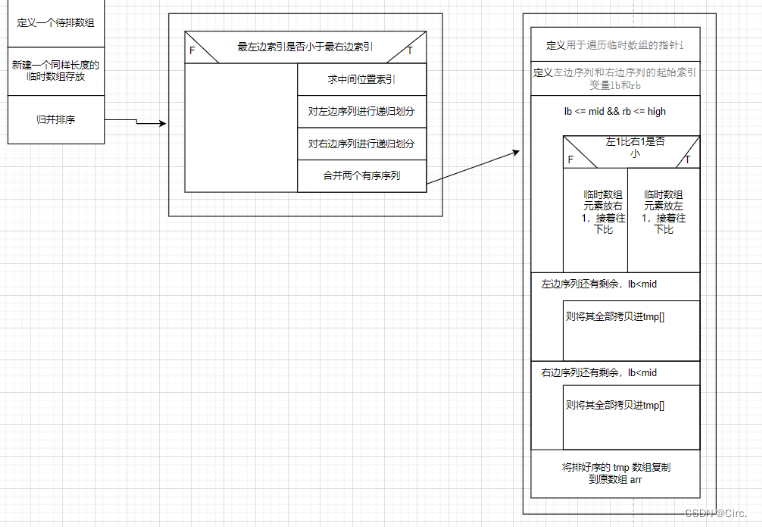
public static void mergeSort(int[] arr, int low, int high, int[] tmp) {
if (low < high) {
// 求中间位置,用于将数组拆分成两部分
int mid = (low + high) / 2;
//对左边序列递归划分
mergeSort(arr, low, mid, tmp);
//对右边序列进行递归划分
mergeSort(arr, mid + 1, high, tmp);
//合并两个有序序列
merge(arr, low, mid, high, tmp);
}
}
public static void merge(int[] arr, int low, int mid, int high, int[] tmp) {
// 用于遍历 tmp 数组的指针
int i = 0;
//左边序列和右边序列起始索引
int j = low, k = mid + 1;
// 比较左右两个有序数组的元素,并按大小依次放入 tmp 数组中
while (j <= mid && k <= high) {
//左半区第一个元素小于右半区第一个元素
if (arr[j] < arr[k]) {
//接着往后继续比
tmp[i++] = arr[j++];
}
//右半区第一个元素更小,先放右半区第一个元素
else {
tmp[i++] = arr[k++];
}
// // 输出排序过程中数组 arr 的变化
System.out.println(Arrays.toString(arr));
}
//若左边序列还有剩余,则将其全部拷贝进tmp[]中
while (j <= mid) {
tmp[i++] = arr[j++];
}
while (k <= high) {
tmp[i++] = arr[k++];
}
// 将排好序的 tmp 数组复制到原数组 arr 中
for (int t = 0; t < i; t++) {
arr[low + t] = tmp[t];
}
}
}
拓展:
递归和迭代
递归和迭代都是解决问题的方法。递归是通过不断调用自身来解决问题,迭代是通过重复执行相同的操作来解决问题。
递归和迭代的主要区别在于它们的实现方式和执行过程。在递归中,程序通过调用自身来解决问题。递归函数将问题划分为子问题,并将这些子问题交给自身来解决。递归函数必须有一个终止条件,否则它将无限地调用自身,导致程序崩溃。
在迭代中,程序通过重复执行相同的操作来解决问题。迭代通常使用循环结构来实现。在每次迭代中,程序会执行相同的操作,直到达到问题的解决条件为止。迭代的优点是可以使用较少的内存,而且通常比递归更快。
递归和迭代都有各自的优点和缺点。递归通常比较容易理解和实现,但是由于每次递归都会创建新的函数调用栈,因此会消耗较多的内存。迭代通常需要较少的内存,但是实现起来可能比较困难,特别是对于复杂的算法来说。