洛谷 P2782 友好城市线性DP 最长上升子序列二分查找 lower

洛谷 P2782 友好城市线性DP 最长上升子序列二分查找 lower_bound

news2024/11/18 8:31:35

🍑 算法题解专栏

🍑 洛谷：友好城市

题目描述

有一条横贯东西的大河，河有笔直的南北两岸，岸上各有位置各不相同的N个城市。北岸的每个城市有且仅有一个友好城市在南岸，而且不同城市的友好城市不相同。每对友好城市都向政府申请在河上开辟一条直线航道连接两个城市，但是由于河上雾太大，政府决定避免任意两条航道交叉，以避免事故。编程帮助政府做出一些批准和拒绝申请的决定，使得在保证任意两条航道不相交的情况下，被批准的申请尽量多。

输入格式

第1行，一个整数N，表示城市数。

第2行到第n+1行，每行两个整数，中间用一个空格隔开，分别表示南岸和北岸的一对友好城市的坐标。

输出格式

仅一行，输出一个整数，表示政府所能批准的最多申请数。

样例 #1

样例输入 #1

样例输出 #1

提示

50% 1<=N<=5000,0<=xi<=10000

100% 1<=N<=2e5,0<=xi<=1e6

🍑 题意

🍤 每个城市只能建立一座桥
🍤 桥不能交叉：

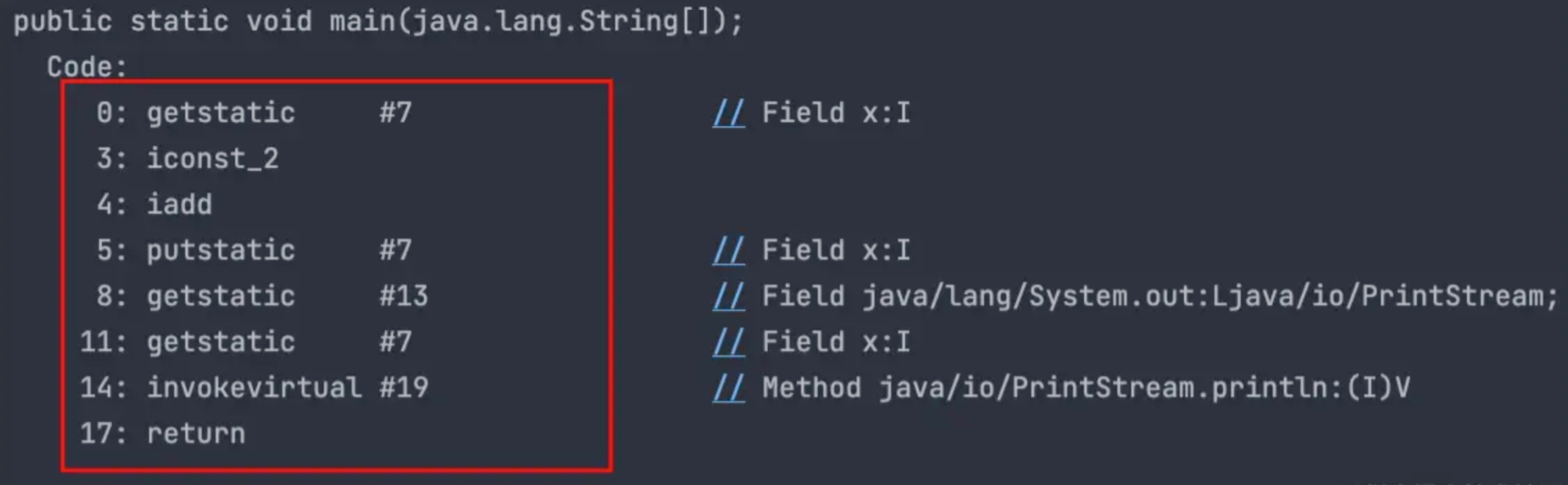
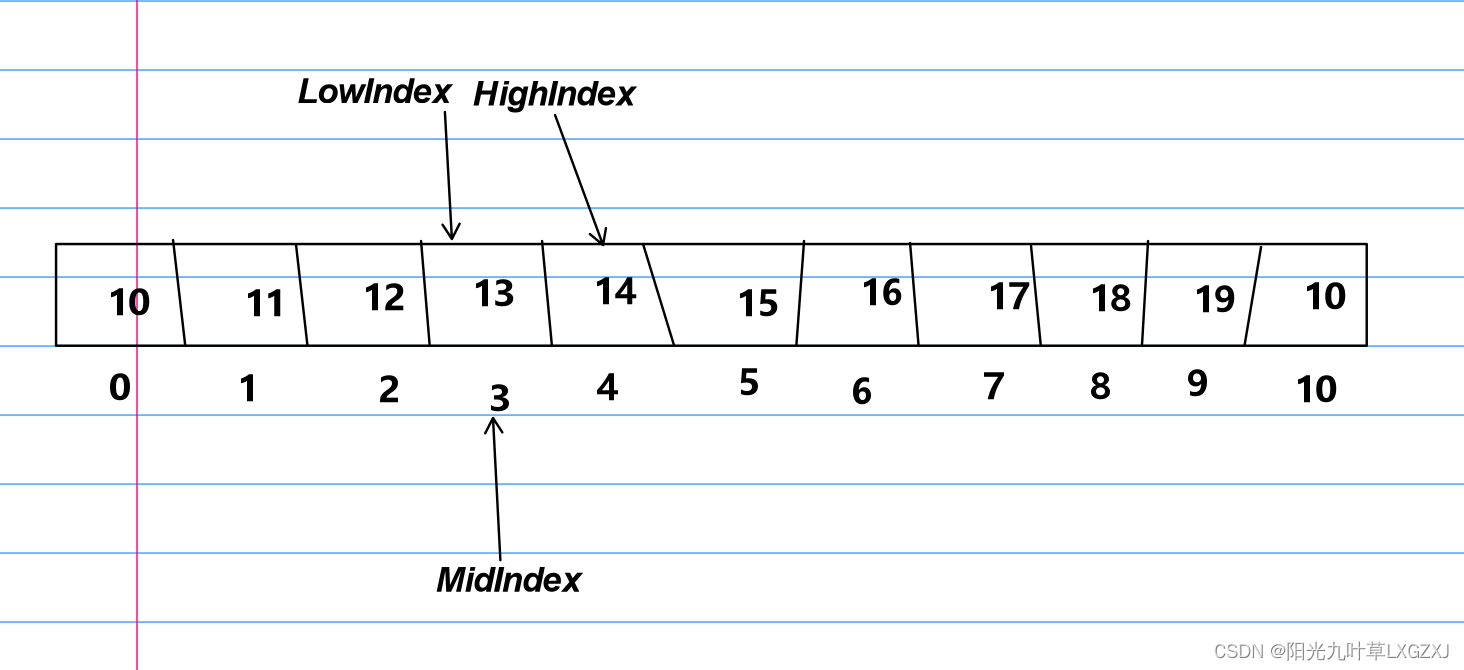
🍑 Arrays.BinarySort(数组，起点，终点（不包含），待查找的值）
👨‍🏫 参考文档

在这里插入图片描述
🍑 insert point（插入点）

🍤 初始化
数组 a {1，3，5，7}
查找值：4 
🍤 实测出真知
BinarySort(a,4) == -3
设 insert point 为 x
则 -x - 1 = -3  --> x = -(-3 + 1) = 3
👨‍🏫 为什么插入点是 3 呢
假设：4 已经插入到数组了，则 a = {1，3，4，5，7}
可见：第一个大于 4 的元素5 的下标为

🍑 输入数据量过多，使用快读
🍑 扩展：C++ STL 中的 lower_bound 参考

有序的情况下，lower_bound返回指向第一个值不小于val的位置
也就是返回第一个大于等于val值的位置。（通过二分查找）

import java.io.*;
import java.util.*;

public class Main
{
	static int N = 200010;
	static Pair[] a = new Pair[N];
	static int[] f = new int[N]; // f[i]=长度为i的IS最小最后一个数

	static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));

//	友好城市类
	static class Pair
	{
		int l, r;

		Pair(int l, int r)
		{
			this.l = l;
			this.r = r;
		}
	}

//	在数组中找到 >= x 的所有数中的最小值(下标) // 手动实现 lowerBound
	static int binarySearch(int[] a, int l, int r, int x)
	{
		while (l < r)
		{
			int m = l + r >> 1;
			if (a[m] < x)
				l = m + 1;
			else
			{
				r = m;
			}
		}
		return l;
//		if (l == r)
//			return l;
//		int m = l + r + 1 >> 1;
//		if (x > a[m])// m 符合条件,结果在右区间
//			return binarySearch(a, m, r, x);
//		else// m 不符合条件,结果在左区间
//		{
//			return binarySearch(a, l, m - 1, x);
//		}
	}

	public static void main(String[] args) throws IOException
	{
//		Scanner sc = new Scanner(System.in);
//		int n = sc.nextInt();
		int n = Integer.parseInt(in.readLine());
		int p = 0;
		for (int i = 0; i < n; i++)
		{
			String[] ss = in.readLine().split(" ");
			int l = Integer.parseInt(ss[0]);
			int r = Integer.parseInt(ss[1]);

//			int l = sc.nextInt();
//			int r = sc.nextInt();
			a[i] = new Pair(l, r);
		}

		Arrays.sort(a, 0, n, (o1, o2) -> o1.l - o2.l);

		for (int i = 0; i < n; i++)
		{
			if (a[i].r > f[p])
			{
				p++;
				f[p] = a[i].r;
			} else
			{
//				int pos = Arrays.binarySearch(f, 1, p + 1, a[i].r);// AC
				int pos = binarySearch(f, 1, p, a[i].r); //手动实现
				if (pos < 0)// 加一层保险
					pos = -(pos + 1);// 本题保证了城市不会重复，所以可以直接按返回 -(插入点-1) 处理
				f[pos] = a[i].r;
			}
		}
		System.out.println(p);
	}
}

🍑 暴力线性DP O(n^2) （50%）

import java.util.Arrays;
import java.util.Scanner;

public class Main
{
	static int N = (int) 2e5 + 10;
	static Pair[] w = new Pair[N];
	static int[] f = new int[N];

	static class Pair
	{
		int x;
		int y;

		public Pair(int x, int y)
		{
			super();
			this.x = x;
			this.y = y;
		}
	}

	public static void main(String[] args)
	{
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();
		for (int i = 0; i < n; i++)
		{
			int x = sc.nextInt();
			int y = sc.nextInt();
			w[i] = new Pair(x, y);
		}
		Arrays.sort(w, 0, n, (o1, o2) -> o1.y - o2.y);

//		DP
		int res = 0;
		for (int i = 0; i < n; i++)
		{
			f[i] = 1;
			for (int j = 0; j < i; j++)
				if (w[j].x < w[i].x)
					f[i] = Math.max(f[i], f[j] + 1);
			res = Math.max(res, f[i]);
		}

		System.out.println(res);
	}
}