目录
一、概念
1、查找表
2、关键字
3、主关键字
4、次关键字
二、查找表分类
1、静态查找表
2、动态查找表
三、平均查找长度
四、顺序查找
1、适用范围
2、结构体定义
3、函数定义
(1)生成测试数据(创建顺序查询表)
(2)无哨兵
(3)有哨兵
五、折半查找
1、非递归
2、递归
六、Linux环境编译测试
一、概念
1、查找表
由同一类型的数据元素构成的集合。
2、关键字
用来标识一个数据元素的某个数据项的值。
3、主关键字
可唯一地标识一个记录的关键字。
4、次关键字
用以识别若干记录的关键字。
二、查找表分类
1、静态查找表
仅作查询操作的查找表。
2、动态查找表
作插入和删除操作的查找表。
三、平均查找长度
关键字的平均比较次数,也称为平均查找长度ASL(Average Search Length)。
| 参数名 | 描述 |
| n | 记录的个数。 |
| pi | 查找第i个记录的概率(通常认为pi = 1 / n)。 |
| ci | 记录第i个记录所需的比较次数。 |
四、顺序查找
1、适用范围
(1)顺序表或线性链表表示的静态查找表。
(2)表内元素之间无序。
2、结构体定义
typedef char CharKeyType;
typedef int IntKeyType;
typedef long long int SeqSearchTableSizeType;
typedef long long int ChunkSizeType;
typedef struct SeqSearchTableElemType
{
CharKeyType CharKey;//后续可以放其他类型的数据,不止一个关键域。
SeqSearchTableSizeType NumberKey;
}SeqSearchTableElemType;
//Data的0号位不用,当作哨兵使用
typedef struct SeqSearchTable
{
SeqSearchTableElemType* Data;
SeqSearchTableSizeType Length;
}SeqSearchTable;3、函数定义
(1)生成测试数据(创建顺序查询表)
//生成测试数据使用
Status CreateSeqSearchTable(SeqSearchTable** SST, SeqSearchTableSizeType DataNum, CharKeyType key)
{
JudgeAllNullPointer(SST);
*SST = (SeqSearchTable*)MyMalloc(sizeof(SeqSearchTable));
(*SST)->Data = (SeqSearchTableElemType*)MyMalloc(sizeof(SeqSearchTableElemType) * (DataNum + 1));
(*SST)->Length = DataNum;
SeqSearchTableSizeType i = 1;
SeqSearchTableSizeType j = 65;
for(i = 1; i <= DataNum; i++,j++)
{
if(j > 90)
{
j = 65;
}
(*SST)->Data[i].CharKey = j;
(*SST)->Data[i].NumberKey = i;
}
(*SST)->Data[1].CharKey = key;
Log("Create SeqSearchTable Normal\n",Info);
return SuccessFlag;
}(2)无哨兵
//0:查询不到关键元素。其他值:关键字在SeqSearchTable中的索引位。
SeqSearchTableSizeType SeqSearch(SeqSearchTable* SST, CharKeyType Key)
{
JudgeAllNullPointer(SST);
Log("SeqSearch Start\n", Info);
SeqSearchTableSizeType i;
for(i = SST->Length - 1; i >= 1; i--)
{
if(SST->Data[i].CharKey == Key)
{
return i;
}
}
return 0;
}(3)有哨兵
//0:查询不到关键元素。其他值:关键字在SeqSearchTable中的索引位。
SeqSearchTableSizeType SeqSearchSentry(SeqSearchTable* SST, CharKeyType Key)
{
JudgeAllNullPointer(SST);
Log("SeqSearchSentry Start\n", Info);
SST->Data[0].CharKey = Key;
SeqSearchTableSizeType i;
for(i = SST->Length - 1;; i--)
{
if(SST->Data[i].CharKey == Key)
{
return i;
}
}
}相比于无哨兵,例如需要比较n次才能匹配关键字,可以少判断n次的i >= 1,效率上有一定提升。
五、折半查找
折半查找的效率高于顺序查找,但适用范围仅限于排好序的数据,没有顺序查找适用性广泛。
1、非递归
SeqSearchTableSizeType BinarySearch(SeqSearchTable* SST, SeqSearchTableSizeType NumberKey)
{
JudgeAllNullPointer(SST);
Log("BinarySearch Start\n", Info);
SeqSearchTableSizeType LowIndex = 1;
SeqSearchTableSizeType HighIndex = SST->Length;
SeqSearchTableSizeType MidIndex;
while(LowIndex <= HighIndex)
{
MidIndex = (HighIndex + LowIndex) / 2;
if(SST->Data[MidIndex].NumberKey == NumberKey)
{
return MidIndex;
}
if(SST->Data[MidIndex].NumberKey > NumberKey)
{
HighIndex = MidIndex - 1;
}
else
{
LowIndex = MidIndex + 1;
}
}
return 0;
}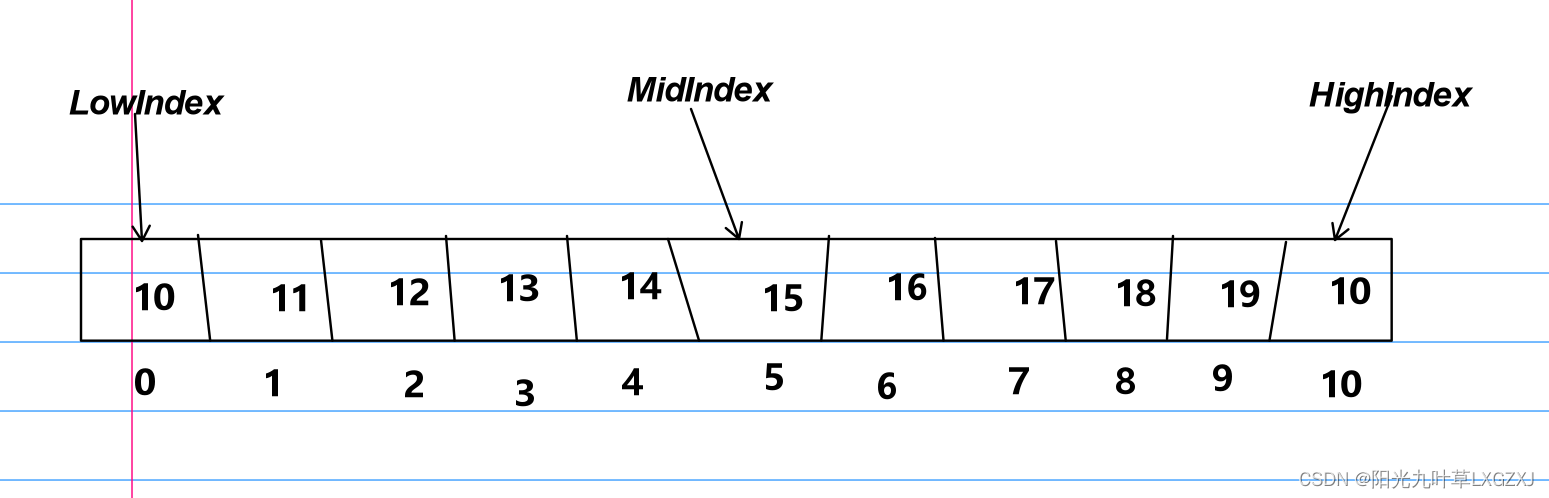
例如我们需要找13,MidIndex = (0 + 10)/ 2 = 5,15比13大。
HighIndex = 5 - 1 = 4;
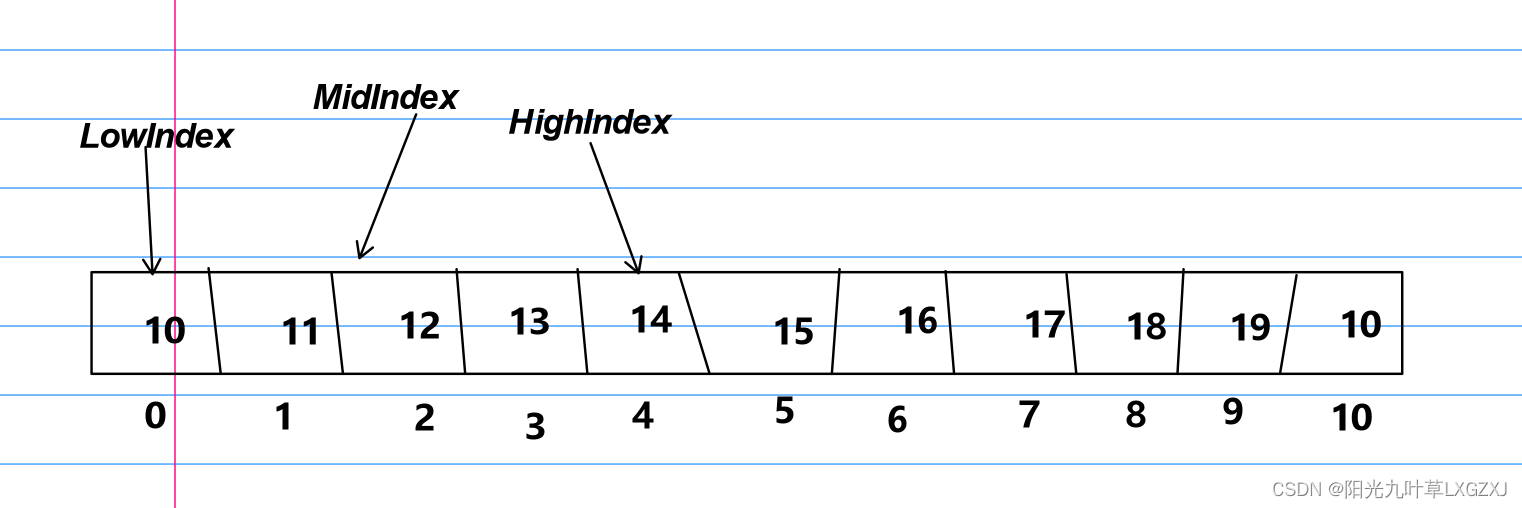
MidIndex = (0 + 4)/ 2 = 2,12比13小。LowIndex = 2 + 1 = 3;
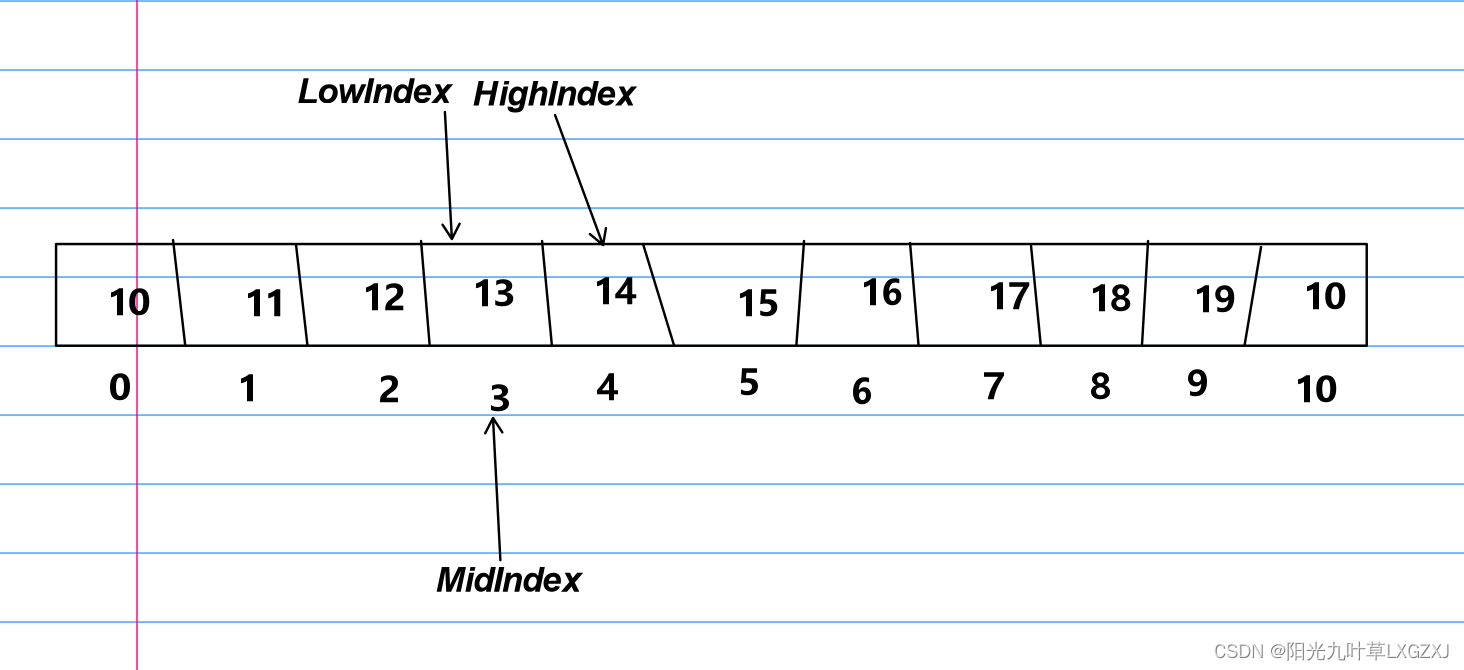
MidIndex = (3 + 4)/ 2 = 3,找到关键字13。
2、递归
SeqSearchTableSizeType BinarySearchRecursion(SeqSearchTable* SST, SeqSearchTableSizeType NumberKey, SeqSearchTableSizeType LowIndex, SeqSearchTableSizeType HighIndex)
{
if(LowIndex > HighIndex)
{
return 0;
}
SeqSearchTableSizeType MidIndex = (HighIndex + LowIndex) / 2;
if(SST->Data[MidIndex].NumberKey == NumberKey)
{
return MidIndex;
}
else if(SST->Data[MidIndex].NumberKey > NumberKey)
{
HighIndex = MidIndex - 1;
return BinarySearchRecursion(SST, NumberKey, LowIndex, HighIndex);
}
else
{
LowIndex = MidIndex + 1;
return BinarySearchRecursion(SST, NumberKey, LowIndex, HighIndex);
};
}递归先写退出条件再写逻辑关系,其实每一步都是折半查找,总体思路和上面差的不多,这里就不多赘述了。
六、Linux环境编译测试
[gbase@czg2 Select]$ make
gcc -Wall -Wextra -O3 ../Log/Log.c ../PublicFunction/PublicFunction.c Select.c HashTable.c AvlTree.c main.c -o TestSelect -I ../Log/ -I ../PublicFunction/ -I ./ -I ../PublicFunction/SqStack/
[gbase@czg2 Select]$ ./TestSelect
[2023-5]--[ Info ]--Create SeqSearchTable Normal
[2023-5]--[ Info ]--SeqSearch Start
[2023-5]--[ Info ]--Index : 1, Elapsed Time : 0 ms
[2023-5]--[ Info ]--SeqSearchSentry Start
[2023-5]--[ Info ]--Index : 1, Elapsed Time : 0 ms
[2023-5]--[ Info ]--BinarySearch Start
[2023-5]--[ Info ]--Index : 3, Elapsed Time : 0 ms
[2023-5]--[ Info ]--BinarySearchRecursion Start
[2023-5]--[ Info ]--Index : 3, Elapsed Time : 0 ms