一、概述
朴素贝叶斯算法是典型的有监督学习算法,解决的是分类问题
贝叶斯算法是一种基于贝叶斯定理的分类算法,它的优点和缺点如下:
优点:
- 算法原理简单易懂,实现较为容易;
- 可以利用先验知识对模型进行训练,并不需要大量的数据就可以得到合理的预测结果;
- 对噪声数据具有鲁棒性,因为模型可以自动学习并忽略噪声数据;
能够处理多分类问题。
缺点:
- 需要先验知识作为输入,若先验信息不准确,则会影响模型的预测结果;
- 在输入变量的数量很大时,计算复杂度会非常高,需要耗费大量的时间和计算资源;
- 对连续型变量的建模较难,需要对其进行离散化处理,这样就可能会丢失一些信息;
- 当特征之间存在相互关联时,贝叶斯算法的表现可能会受到限制。
二、什么是贝叶斯?
-
贝叶斯是指贝叶斯学派(Bayesian),它是概率论的一个分支,其研究的是不确定性的量化和推理。具体来说,贝叶斯学派的核心思想是基于贝叶斯公式进行不确定性推断。
-
贝叶斯公式是概率论中的一项基本定理,它描述了在给定某些先验条件下,根据新的观测数据如何更新已有的信念。简单地说,贝叶斯公式可以用来计算在得到新信息后,对事件可能发生的概率进行修正。
-
贝叶斯学派认为,我们对未知事物的判断应该基于主观经验和现有证据,而非仅仅依赖于观测数据。因此,在贝叶斯学派的框架下,我们可以将个人经验和领域知识作为先验知识输入到模型中,然后根据新的数据来不断调整我们的信念,最终得出更加准确的结论。
-
贝叶斯方法在机器学习、统计学和人工智能等领域中得到广泛的应用,例如朴素贝叶斯分类、贝叶斯网络、马尔可夫链蒙特卡洛(MCMC)等算法。
三、朴素贝叶斯与贝叶斯决策论的关系
- 朴素贝叶斯算法是基于贝叶斯决策论的一种
分类算法。 - 贝叶斯决策论是指给定一个待分类的样本,通过其
先验概率和各个特征的条件概率来计算样本属于某个类别的后验概率,从而得到最终的分类结果。 - 而朴素贝叶斯算法
假设各个特征之间相互独立,通过计算每个特征对于不同类别的条件概率来得到最终的分类结果。因此,朴素贝叶斯算法是一种基于贝叶斯决策论并且做出了条件独立性假设的分类算法。
例如:假设
现在有两组样本数据,我们使用p1(x,y)表示样本数据一中数据点(x,y),用p2(x,y)表示样本数据二中的数据点(x,y)。
- 如果p1(x,y) > p2(x,y),那么类别为1
- 如果p1(x,y) < p2(x,y),那么类别为2
也就是说,我们会选择高概率对应的类别。这就是贝叶斯决策理论的核心思想,即选择具有最高概率的决策。
已经了解了贝叶斯决策理论的核心思想,那么接下来,就是学习如何计算p1和p2概率。
四、贝叶斯理论推导.
经过上面的例子我们清楚,贝叶斯决策论是指给定一个待分类的样本,通过其先验概率和各个特征的条件概率来计算样本属于某个类别的后验概率,从而得到最终的分类结果,因此计算p1和p2是我们的最终目的。
计算这两概率就绕不开条件概率,因为贝叶斯算法利用了条件概率来做出决策.
1.条件概率
指在事件B发生的情况下,事件A发生的概率,用P(A|B)来表示。
例如:
圆A与圆B相交,进行推导条件概率:

2. 全概率公式:
条件该率只是帮助我们进行部分内容计算,而想要最终的概率结果,仍然需要进行全概率公式计算:
进行简单推导

3.进行最后计算:
经过上面的条件概率和全概率推导最后得到:
p(A|B) = p(A)p(B|A)/p(B)
我们把P(A)称为"先验概率"(Prior probability),即在B事件发生之前,我们对A事件概率的一个判断。
P(A|B)称为"后验概率"(Posterior probability),即在B事件发生之后,我们对A事件概率的重新评估。
P(B|A)/P(B)称为"可能性函数"(Likelyhood),这是一个调整因子,使得预估概率更接近真实概率。
总结为:
后验概率 = 先验概率 x 调整因子
这就是贝叶斯推断的含义。我们先预估一个"先验概率",然后加入实验结果,看这个实验到底是增强还是削弱了"先验概率",由此得到更接近事实的"后验概率"。
在这里,如果"可能性函数"P(B|A)/P(B)>1,意味着"先验概率"被增强,事件A的发生的可能性变大;如果"可能性函数"=1,意味着B事件无助于判断事件A的可能性;如果"可能性函数"<1,意味着"先验概率"被削弱,事件A的可能性变小。
用一个实际例子来说明:

4. 推广到朴素贝叶斯的
上面有说到,朴素贝叶斯与贝斯是不同的。
朴素贝叶斯分类器是一种基于贝叶斯定理和条件独立假设的分类器。它假设每个特征之间相互独立,即每个特征对于分类结果的影响是相互独立的。这样可以大大简化模型的训练和预测,并提高计算效率。
贝叶斯的去噪则是一种基于最大后验概率估计(MAP)的方法,用于去除数据中的噪声。在贝叶斯的去噪中,我们将原始信号看作是随机变量,将噪声看作是先验概率分布,利用贝叶斯定理推导出后验概率分布。然后,根据后验概率分布进行信号恢复。与朴素贝叶斯不同,贝叶斯的去噪并没有使用条件独立假设。
相比较而言,贝叶斯算法不涉及特征和类别之间的关系,只是通过统计方法来预测某个事件的概率;而朴素贝叶斯算法则是基于特征条件独立性假设,利用贝叶斯定理来进行分类决策。
用公式说明就是:

这里说明一下为什么缺少了p(B)
我们看到朴素贝叶斯在使用的时候相对于贝叶斯缺少了p(B)
-
贝叶斯公式中的p(A|B)表示在已知事件 B 发生的情况下,事件 A 发生的概率。而朴素贝叶斯是一种基于贝叶斯公式的分类算法,在分类问题中,将特征向量看作一个事件 B,将类别看作一个事件A。 -
因此,在计算
样本 x属于某个类别 C的后验概率时,朴素贝叶斯假设各个特征之间相互独立,即p(x|C) = p(x1|C)p(x2|C)...p(xn|C),其中x1, x2, ..., xn分别是特征向量的不同维度。这个假设简化了计算过程,但是忽略了特征之间的相关性。
说明一下这里的不同维度是什么意思?
不同维度指的是一个特征向量中不同的特征值,例如对于一个文本分类问题,可以将每个单词作为一个特征,那么一个特征向量就可以表示为一个包含多个单词出现次数的向量。这个向量的每个维度就代表一个单词在该文本中的出现次数,也就是一个特征值。因此,在朴素贝叶斯中,p(x|C) 表示给定类别 C 下,各个特征值(维度)之间相互独立的条件概率。 -
根据贝叶斯公式,
朴素贝叶斯可表示为:p(C|x) = p(x|C)p(C)/p(x)其中,p(x|C)表示在类别C下特征向量 x 出现的概率,p(C)表示类别C 的先验概率,p(x)表示特征向量出现的概率。由于对于所有类别都是相同的,所以可以省略分母 p(x)。 -
因此,
朴素贝叶斯的公式可以简化为:p(C|x) ∝ p(x|C)p(C)其中,∝ 表示“正比于”。这个式子中缺少了p(x),但是在分类问题中,对于一个给定的样本x,p(x)对于不同的类别来说是相同的,因此省略掉后不影响最终的分类结果。
6. 示例说明
某个医院早上来了六个门诊的病人,他们的情况如下表所示:
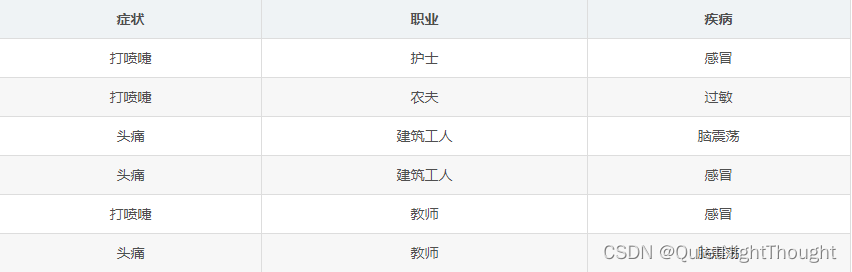 现在又来了第七个病人,是一个打喷嚏的建筑工人。请问他患上感冒的概率有多大?
现在又来了第七个病人,是一个打喷嚏的建筑工人。请问他患上感冒的概率有多大?
根据贝叶斯定理:

根据朴素贝叶斯条件独立性的假设可知,"打喷嚏"和"建筑工人"这两个特征是独立的,因此,上面的等式就变成了

这里可以计算:
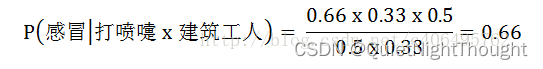
因此,这个打喷嚏的建筑工人,有66%的概率是得了感冒。同理,可以计算这个病人患上过敏或脑震荡的概率。比较这几个概率,就可以知道他最可能得什么病。
这就是贝叶斯分类器的基本方法:在统计资料的基础上,依据某些特征,计算各个类别的概率,从而实现分类。
同样,在编程的时候,如果不需要求出所属类别的具体概率,P(打喷嚏) = 0.5和P(建筑工人) = 0.33的概率是可以不用求的。
参考文章