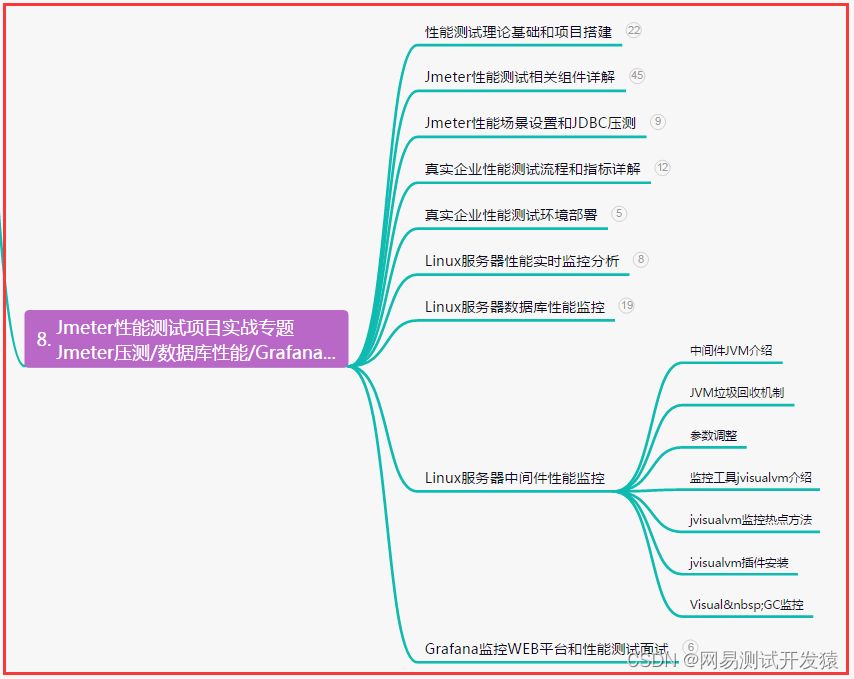
插入排序
- 1. 排序
- 2.插入排序
- 2.1直接插入排序
- 2.2折半插入法
- 2.3希尔排序
1. 排序
-
排序的概念
排序就是将一组杂乱无章的数据按一定规律(顺序或者逆序)排列起来。 -
排序的目的
方便查找元素。 -
内部排序和外部排序
若待排序记录都在内存中,称为内部排序;若待排序记录一部分在内存,一部分在外存,则称为外部排序。 -
稳定性
有两个相同的数据,在排序前后的前后顺序不变。它与时间复杂度和空间复杂度可以用来的衡量算法的好坏。
2.插入排序
2.1直接插入排序
-
将待排数据按其关键码的大小插入到一个有序序列中,最终将所有数据插入序列中,形成一个新的有序序列。
-
边插入边排序

-
代码实现
//直接插入排序(以排升序为例子)
void InsertSort(int* arr,int n)
{
//思路:从第二个数开始,逐个对有序序列排序
int i = 0;
for (i = 1; i < n; i++)
{
int end = i - 1;//前面有序序列的最后一个元素
int tmp = arr[i];
while (end >= 0)
{
if (arr[end] > tmp)//如果有序序列的最后一个元素大于要插入的元素,往后移一位
{
arr[end + 1] = arr[end];
end--;
}
else//最后一个元素小于或者等于要插入的元素,跳出循环
{
break;
}
}
//遇到特殊情况:要插入元素小于有序序列中的任何元素
arr[end + 1] = tmp;//既能处理要插入元素比前一个大的情况,又能处理end<0的情况
}
}
- 分析
时间复杂度
最好情况下,数据本就是有序的,每次只需与前一个元素比较一次即可,时间复杂度是O(N);最坏情况下,第i趟比较i次,且移动i+1次,时间复杂度是O(N^2)。
空间复杂度
只有开辟一个额外临时空间。空间复杂度是O(1)。
稳定性
上面的例子中有相同的12,能保证后面的12始终在后面。是一种稳定的算法
缺点
比较次数过多,影响效率。所以就有了折半插入排序。
2.2折半插入法
- 思想
在有序序列中寻找中间进行比较,减少比较次数。 - 展示
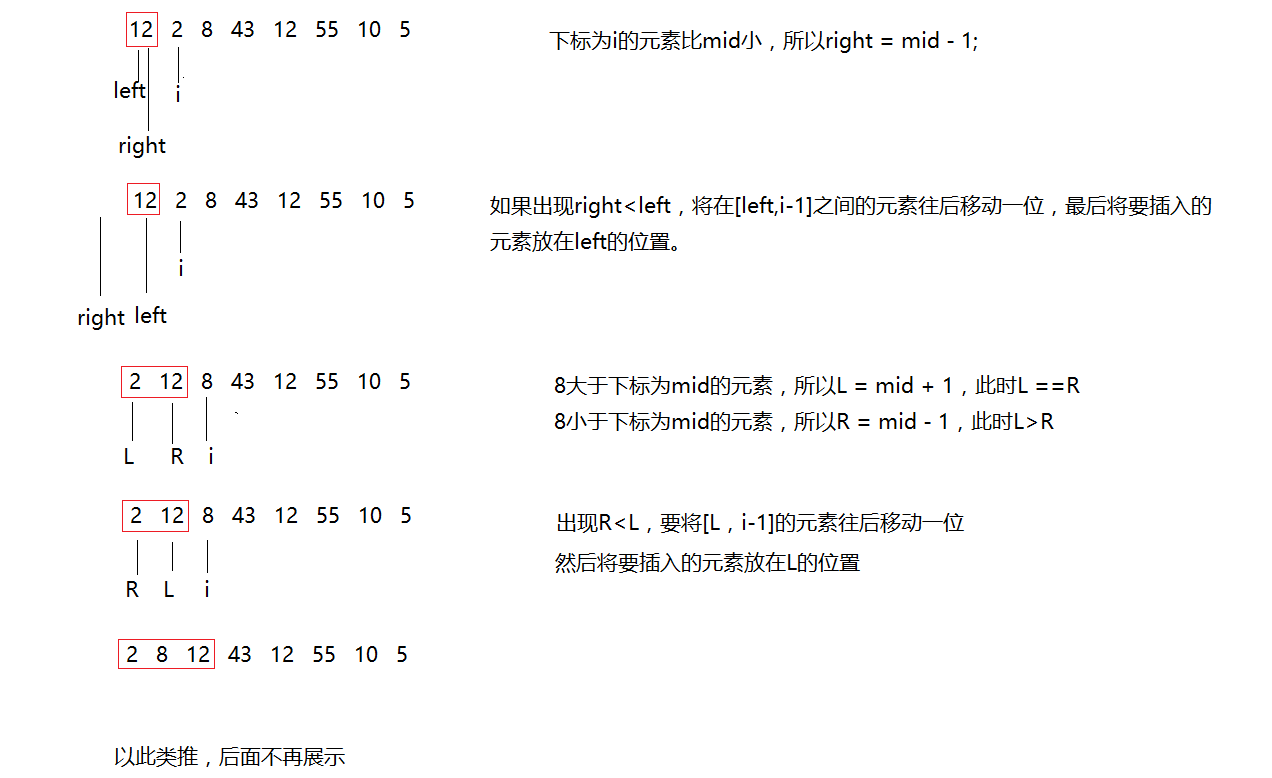
- 代码实现
//折半插入法(以升序为例)
void BInsertSort(int* arr, int n)
{
for (int i = 1; i < n; i++)
{
int tmp = arr[i];
int left = 0;
int right = i - 1;
while (left <= right)
{
int mid = (left + right) / 2;
if (arr[mid] > arr[i])
{
right = mid - 1;
}
else
{
left = mid + 1;
}
}
for (int j = i - 1; j >= left; j--)
{
arr[j + 1] = arr[j];
}
arr[left] = tmp;
}
}
- 分析
时间复杂度
在最好情况下,也就是数据是有序时,还是要进行折半比较,比较次数相交于直接插入多;在最坏情况下,比较次数减少明显,在logN这个量级。但是移动次数保持不变,所以时间复杂度依旧是O(N^2)。
空间复杂度
只申请一个额外空间。空间复杂度是O(1)。
稳定性
在排序前后两个相等的数据前后顺序不变。
2.3希尔排序
-
思想
首先先对数据进行分组,将每组进行直接插入排序,这是预排序。待数据基本有序时,就对全体数据进行直接插入排序。 -
例子

-
疑惑
那我们要如何确定gap的大小?gap减少到多少时可以算基本有序?
这个没有明确规定。gap越大,数据跳得越快,越不接近有序,gap越小,数据跳得越慢,越接近有序。gap是个渐变的数,越来越小,最后必须为1。这样才能保证数据最终为有序。gap一般为数据的数目,再以1/2的倍数在减小。 -
代码实现
//希尔排序
void ShellSort(int* arr, int n)
{
int gap = n;
while (gap > 1)
{
//gap /= 2;
gap = gap / 3 + 1;//+1保证最后进行一次排序是直接插入排序
for (int i = 0; i < n - gap; i++)
{
int end = i;
int tmp = arr[i + gap];
while (end >= 0)
{
if (tmp < arr[end])
{
arr[end + gap] = arr[end];
end -= gap;
}
else
{
break;
}
}
arr[end + gap] = tmp;
}
}
}
- 算法分析
时间 复杂度
最外层的while循环的时间复杂度是O(logN),因为N是以1/2在减少。在for循环刚开始时,gap很大,当gap=n/3+1时,for的执行次数是n/3,for里面的while的执行次数为1+2+3 = 6(以最坏情况看),所以第一次循环的时间复杂度是6*(n/3) = 2n。第二次循环,gap接近于n/9,此时for循环的执行次数是n/9,for里面的while的执行次数是1+2+……+9 = 45,所以第二次循环的执行次数是45*(n/9) = 5n。(但实际上要小于5n,因为上次循环数据已经比原先接近有序,所以还要考虑上一轮排序的影响)。当gap最终为1时,因为经过前面多轮的预排序,数据已经接近有序,可以近似于有序序列的排序,所以时间复杂度是O(N)。
综上,根据大量资料可得,希尔排序的时间复杂度是O(n^1.25)~O(1.6n ^1.25),仍然是处于O(NlongN)这个量级,所以时间复杂度是O(NlogN)。
空间复杂度
仅开辟一个额外空间,所以空间复杂度是O(1)。
稳定性
这是一个不稳定的排序。因为会对数据进行分组,相同的数据在不同的组里面的最终顺序不同,可能导致最后两者的前后顺序不同。
注意
在数据接近有序时,直接插入排序的效率比这版插入排序和希尔排序的效率要高。