今天先搞题目

给你一个points 数组，表示 2D 平面上的一些点，其中 points[i] = [xi, yi] 。

连接点 [xi, yi] 和点 [xj, yj] 的费用为它们之间的 曼哈顿距离 ：|xi - xj| + |yi - yj| ，其中 |val| 表示 val 的绝对值。

请你返回将所有点连接的最小总费用。只有任意两点之间 有且仅有 一条简单路径时，才认为所有点都已连接。

示例 1：

输入：points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
输出：20
解释：

我们可以按照上图所示连接所有点得到最小总费用，总费用为 20 。
注意到任意两个点之间只有唯一一条路径互相到达。
示例 2：

输入：points = [[3,12],[-2,5],[-4,1]]
输出：18
示例 3：

输入：points = [[0,0],[1,1],[1,0],[-1,1]]
输出：4
示例 4：

输入：points = [[-1000000,-1000000],[1000000,1000000]]
输出：4000000
示例 5：

输入：points = [[0,0]]
输出：0
 

提示：

1 <= points.length <= 1000
-106 <= xi, yi <= 106
所有点 (xi, yi) 两两不同。

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/min-cost-to-connect-all-points
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

没啥可讲的,就是一个最小生成树的模板题目

我复习一下,写着写着差点没缓过来,写成了djs,好久没写了,记得是咋回事可是写起来就不太对了

要多写了呀直接哭死了.

int minCostConnectPoints(int** points, int pointsSize, int* pointsColSize){
    int map[pointsSize+1][pointsSize+1];
    for(int j=1;j<=pointsSize;j++)
    memset(map[j],0,sizeof(int)*(pointsSize+1));

    for(int h=0;h<pointsSize;h++){
        for(int g=0;g<pointsSize;g++){
            if(g!=h){
            map[h+1][g+1]=abs(points[h][0]-points[g][0])+abs(points[h][1]-points[g][1]);
            map[g+1][h+1]=abs(points[h][0]-points[g][0])+abs(points[h][1]-points[g][1]);
            }
        }
    }
    int* maps = (int*)malloc(sizeof(int)*(pointsSize+1));
    memset(maps,0,sizeof(int)*(pointsSize+1));
 
    int* lst = (int*)malloc(sizeof(int)*(pointsSize+1));
    memset(lst,0,sizeof(int)*(pointsSize+1));
    maps[1]=1;
    int ans=0;
    for(int h=1;h<pointsSize+1;h++){
        lst[h]=map[1][h];
    }

    for(int k=0;k<pointsSize-1;k++){
          int max=99999999;
          int l=0;
         for(int j=1;j<=pointsSize;j++){
             if(lst[j]<max&&lst[j]!=0&&maps[j]==0){
                 max=lst[j];
                 l=j;
             }
         }
         ans+=max;
         maps[l]=1;
         for(int h=1;h<pointsSize+1;h++){
              if(map[l][h]<lst[h]&&maps[h]==0)
              lst[h]=map[l][h];
         }
    }
    return ans;

}

 直接想出来的,呀哈想了一会写出来了

2106. 摘水果

难度困难123收藏分享切换为英文接收动态反馈

在一个无限的 x 坐标轴上，有许多水果分布在其中某些位置。给你一个二维整数数组 fruits ，其中 fruits[i] = [positioni, amounti] 表示共有 amounti 个水果放置在 positioni 上。fruits 已经按 positioni 升序排列 ，每个 positioni 互不相同 。

另给你两个整数 startPos 和 k 。最初，你位于 startPos 。从任何位置，你可以选择 向左或者向右 走。在 x 轴上每移动 一个单位 ，就记作 一步 。你总共可以走 最多 k 步。你每达到一个位置，都会摘掉全部的水果，水果也将从该位置消失（不会再生）。

返回你可以摘到水果的 最大总数 。

示例 1：

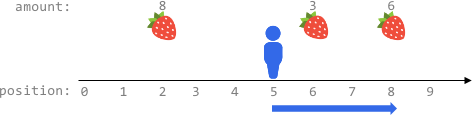
输入：fruits = [[2,8],[6,3],[8,6]], startPos = 5, k = 4
输出：9
解释：
最佳路线为：
- 向右移动到位置 6 ，摘到 3 个水果
- 向右移动到位置 8 ，摘到 6 个水果
移动 3 步，共摘到 3 + 6 = 9 个水果

示例 2：

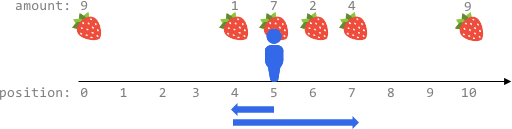
输入：fruits = [[0,9],[4,1],[5,7],[6,2],[7,4],[10,9]], startPos = 5, k = 4
输出：14
解释：
可以移动最多 k = 4 步，所以无法到达位置 0 和位置 10 。
最佳路线为：
- 在初始位置 5 ，摘到 7 个水果
- 向左移动到位置 4 ，摘到 1 个水果
- 向右移动到位置 6 ，摘到 2 个水果
- 向右移动到位置 7 ，摘到 4 个水果
移动 1 + 3 = 4 步，共摘到 7 + 1 + 2 + 4 = 14 个水果

示例 3：

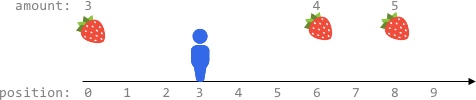
输入：fruits = [[0,3],[6,4],[8,5]], startPos = 3, k = 2
输出：0
解释：
最多可以移动 k = 2 步，无法到达任一有水果的地方

提示：

• 1 <= fruits.length <= 105
• fruits[i].length == 2
• 0 <= startPos, positioni <= 2 * 105
• 对于任意 i > 0 ，positioni-1 < positioni 均成立（下标从 0 开始计数）
• 1 <= amounti <= 104
• 0 <= k <= 2 * 105

 这是签到题目,可是我细节注意没到位,漏了点东西 ,老是错就把解题的思路来搞吧

1首先我们是可以先向左,或者向右,剩下的步数反向走,没过原点就按原点算,过了就算当前的点

2要用前缀和来简化对权值的求和

3遍历每个步数,得到的权值,但是有几种的特殊情况

代码先不放了,没对!

java 知识

数据的类型

1.基本数据类型(就是不是指针的类型都是)

2.引用(指针)

this 是一个方法所在地的调用者的地址

如 Scanr s = new Scanr()

此时this为s就是一个地址

构造方法

可以空参也可以带参数构造

 当你写了,构造方法之后,原本默认的初始空参的构造就没了

private 私有的

只可以在本类中才可以调用,基本上用的类里面的set以及get

还有字符串

好多呀不知道咋讲我把笔记留下来吧

 

 

 

 ok,今天到这就算了

哈哈哈嗝