前言

在电机转子位置估算算法中，常常用到锁相环获取磁链信号或反电势信号中的转子位置信息，考虑到包含转子位置信息的磁链信号或反电势信号多被分解在$\alpha ,\beta$轴，以下内容侧重分析适用于该工况的正交锁相环。

1、正交锁相环原理分析

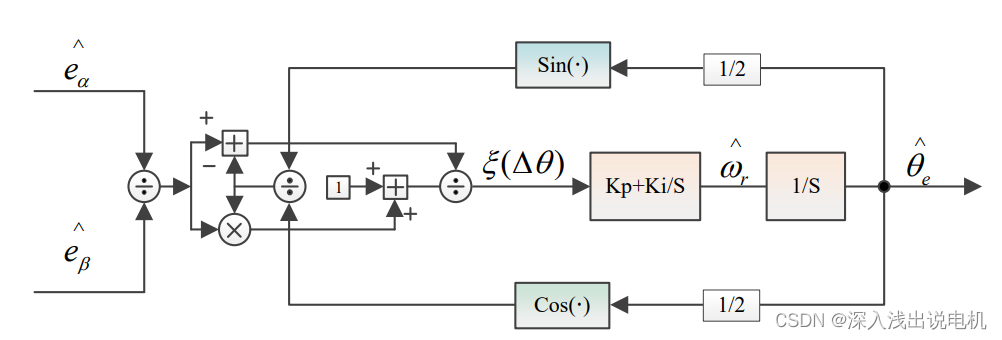
正交锁相环的结构如下图所示：

其中${\hat{e}}_{\alpha },{\hat{e}}_{\beta }$表示$\alpha \beta$轴反电动势。锁相环的输入对$\beta$轴反电动势取反是因为永磁同步机中转子磁链由转子永磁体产生，而反电势是转子磁链的微分，反电势和转子磁链的关系如下:
$$\begin{gathered} e_{\alpha }=\frac{d{\lambda }_{\beta }}{dt}=\frac{d\lambda sin\theta }{dt}=\omega \lambda cos\theta =\omega {\lambda }_{\alpha } \\ {e}_{\beta }=\frac{d{\lambda }_{\alpha }}{dt}=\frac{d\lambda cos\theta }{dt}=-\omega \lambda sin\theta =-\omega {\lambda }_{\beta } \end{gathered}$$

想要了解更多转子位置与反电势或转子磁链的关系请阅读往期文章。
永磁同步电机转子位置估算专题 —— 基波模型与转子位置角

通过上述框图容易看出，正交锁相环是把观测器估算出来的反电势或磁链信号与上一拍计算得到的角度的正余弦结果相乘，然后送到pi调节器，当误差趋于零时，pi的输出即为电机的转速。

要把这句话解释清楚并不容易，这里不得不上公式。

$$\begin{gathered} err=-sin\theta {\lambda }_{\alpha }+cos\theta {\lambda }_{\beta } \\ =-sin\theta \lambda cos\hat{\theta }+cos\theta \lambda sin\hat{\theta } \\ =-\lambda sin\theta cos(\theta +\tilde{\theta })+\lambda cos\theta sin(\theta +\tilde{\theta }) \\ =-\lambda sin\theta (cos\theta cos\tilde{\theta }-sin\theta sin\tilde{\theta })+\lambda cos\theta (sin\theta cos\tilde{\theta }+cos\theta sin\tilde{\theta }) \\ =\lambda sin\theta sin\theta sin\tilde{\theta }+\lambda cos\theta cos\theta sin\tilde{\theta } \\ =\lambda \sin \tilde{\theta } \end{gathered}$$

此处的${\lambda }_{\alpha },{\lambda }_{\beta }$为转子磁链在$\alpha \beta$轴上的分量，若转子磁链分离准确，则可以等效为$\lambda cos\hat\theta,\lambda sin\hat\theta $;$\hat \theta$表示估算角度，考虑到角度是动态变化的，把估算角度进一步写为$(\theta + \tilde \theta)$，$\tilde \theta$表示角度变化量,$\theta$表示上一拍的计算角度。

经过化简，可得pi调节器的输入等价于$\lambda \sin \tilde{\theta }$，当$\tilde{\theta }$非常小时，pi调节器的误差可以进一步简化为$\lambda \tilde{\theta }$，这是一个非常重要的结论，说明pi调节器的误差正比于角度变化量，而角度的变化大小就是速度。

pi调节器的积分可以起到平滑速度的效果，锁相环的pi中ki占的作用大些，kp的作用小些，可以使速度更平滑，kp起的作用越强则速度信号响应越快，在加减速非常快的应用场景下，应该增大锁相环的kp，ki；

到这里我们再思考一个问题，为什么锁相环的kp，ki在一个较大范围内调整，速度都是准确的？

其中的奥妙在于锁相环收敛后，输出的角度是准确的，而角度由速度积分得到，反过来看这个系统更容易理解，就是锁相环收敛后，得到了准确的角度，而电机的转速是锁相环输出角度的微分。

2、锁相环的优缺点

前面说了，锁相环的速度是角度变化率经过pi调节得到的，pi的积分环节会使得速度平滑，而角度由速度积分得到，积分器的输出不会有毛刺，使得角度更加平滑。锁相环输出的角度信号的质量是反正切法远不能极的。

反正切法计算得到了角度，常常对角度进行微分得到速度，微分运算将放大噪声，使得速度信号波动严重，不得不对速度信号进行低通滤波，这样做的结果就是使得速度环的带宽受到较大限制。速度环的计算频率也不得不相对电流环进行较大比例的分频。

锁相环的应用也非百利而无一害，锁相环结构中的pi调节器将引入kp，ki两个待整定参数，在不同应用场景需要进行选择，调的小了将使得角度出现稳态误差，影响动态响应性能，调的大了会放大反电势信号或转子磁链信号的噪声。

锁相环的使用还是要谨慎的。

3、 关于锁相环的拓展思考

锁相环常常作为位置估算算法的一部分出现在电机控制算法工程师的视野，其实锁相环并非只有这么一种使用场景。

正交锁相环适用于需要处理正交信号的多种场合，如旋变编码器、线性hall编码器的测速，等。

锁相环也并非只有正交锁相环一种形式，还有多种变种。此处附上两种抛砖引玉，读者有更多想法欢迎评论区讨论。

该变种对$\alpha \beta$轴反电势信号进行park变换，调节目标为时d轴反电势为零。

该变种对锁相环的输入信号进行预处理，以增大信号的信噪比。

小结

本文分析锁相环的相关原理，并提出自己的见解于诸位讨论，希望能够对各位读者起到帮助，认可作者的工作。

另外做个小广告，欢迎各位大佬关注微信公众号：深入浅出说电机 作者最新文章都首发于公众号。有需要下载参考文献的可以公众号后台回复 QPLLCK 获取下载地址。

参考文献：

Zhang Y, Liu J. An improved Q-PLL to overcome the speed reversal problems in sensorless PMSM drive[C]//2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia). IEEE, 2016: 1884-1888.