第4章-动态规划

总分：100分

得分：100.0分

+ 10.0 分

1 . 多选题 中等 10分

有关0-1背包问题,用c[i][j]描述子问题:1...i共i个物品,背包容量为j的最优值(装入背包的最大价值),则其子问题为:1...i-1共i-1个物品,背包容量为j-w ix i,以下说法正确的是( ABD ) 

A.

当i=0时或j=0时,c[i][j]=0。

B.

当j<w i时,物品无法装入,其x i=0,则背包容量依旧为j,c]i][j]=c[i-1][j].

C.

当j≥w i时,物品可以装入,装呢还是不装呢?这取决于哪个决策能够让c[i][j]最小。故c]i][j]=min(c[i-1][j],c[i-1][j-w i]+v i)

D.

当j≥w i时,物品可以装入,装呢还是不装呢?这取决于哪个决策能够让c[i][j]最大。故c]i][j]=max(c[i-1][j],c[i-1][j-w i]+v i)

 回答正确

解析

暂无解析

老师点评

暂无评语

+ 10.0 分

2 . 多选题 中等 10分

有关最优二叉搜索树说法正确的是( ABD )

A.

最优二叉搜索树的左孩子的节点都比根节点小,右孩子节点都比根节点大。

B.

最优二叉搜索树的平均比较次数最少。

C.

最优二叉搜索树的平均比较次数最多。

D.

最优二叉搜索树中有n个是节点,n+1个虚节点。

3 . 多选题 中等 10分

{s1,s2,...,sn},虚节点{e0,e1,...,en}的最优二叉搜索树问题的子问题描述为有序序列{si,si+1,...,sj},虚节点{ei-1,ei,...,ej}的最优二叉搜索树,以下描述正确的是( ABC )。

A.

i=1，j=n表示规模为n的原问题。

B.

i=j+1，表示字符序列为空，对应的最优二叉搜索树为一棵空树。

C.

有序序列{si,si+1,...,sj},虚节点{ei-1,ei,...,ej}的最优二叉搜索树的子问题是：有序序列{si,si+1,...,sk-1},虚节点{ei-1,ei,...,ek-1}的最优二叉搜索树和有序序列{sk+1,sk+2,...,sj},虚节点{ek,ek+1,...,ej}的最优二叉搜索树。

D.

子问题的最优值：最小平均比较次数c[i][j]，左子树的最优值：最小平均比较次数c[i][k-1]，右子树的最优值：最小平均比较次数c[k+1][j]，三者之间的关系为：c[i][j]=c[i][k-1]+c[k+1][j]+pi+...+pj+qi-1+...+qj

4 . 多选题 中等 10分

有关最长公共子序列问题的动态规划算法说法正确的是( AB )

A.

X n和Y m的代表了两个长度为n和m的字符串,求X n和Y m的最长公共子序列的子问题是:求X i和Y j的最长公共子序列,i=0,1,...n,j=0,1,...,m。

B.

X i和Y j的最长公共子序列当i=0时,最长公共子序列的长度为0;j=0时,最长公共子序列的长度也为0。

C.

设X i和Y j的最长公共子序列的长度c[i][j],求最优值的递归关系式为:c[i][j]=c[i-1][j]。

D.

设X i和Y j的最长公共子序列的长度c[i][j],求最优值的递归关系式为:c[i][j]=c[i-1][j]+1。

5 . 判断题 中等 10分

矩阵连乘问题中有多个矩阵相乘，问题是安排矩阵相乘的先后顺序，使总乘法次数最少，例如 有[A][B]C三个矩阵，则可行的顺序有ABC\ACB\CAB\CBA\BAC\BCA六个。

是  否

6 . 判断题 中等 10分

以动态规划求解0-1背包问题，背包容量可以是任意实数。

是   否

7 . 判断题 中等 10分

最长公共子序列问题中，如果采取穷举法，可以在序列A中子序列可能的开头和结尾（因为子序列由其开头位置和结尾位置唯一确定），然后在序列B中查找它是否存在，如果按照子序列长度降序枚举，找到的第一个公共子序列就是最长公共子序列。

是     否

8 . 判断题 简单 10分

0-1背包问题的动态规划解法不适合背包容量非常大(

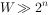
)的情况。

是   否

9 . 判断题 简单 10分

最长公共子序列问题的动态规划解法时间复杂度等于两个序列长度之积。

是  否

 

10 . 判断题 简单 10分

0-1背包问题的贪心法解法和动态规划解法都能够生成最优解。

是   否