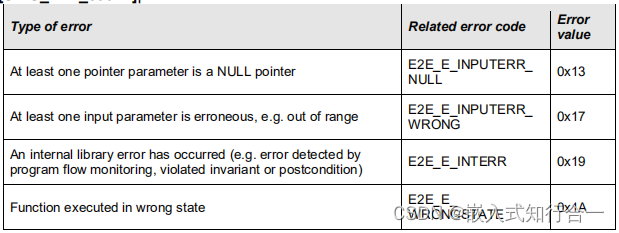
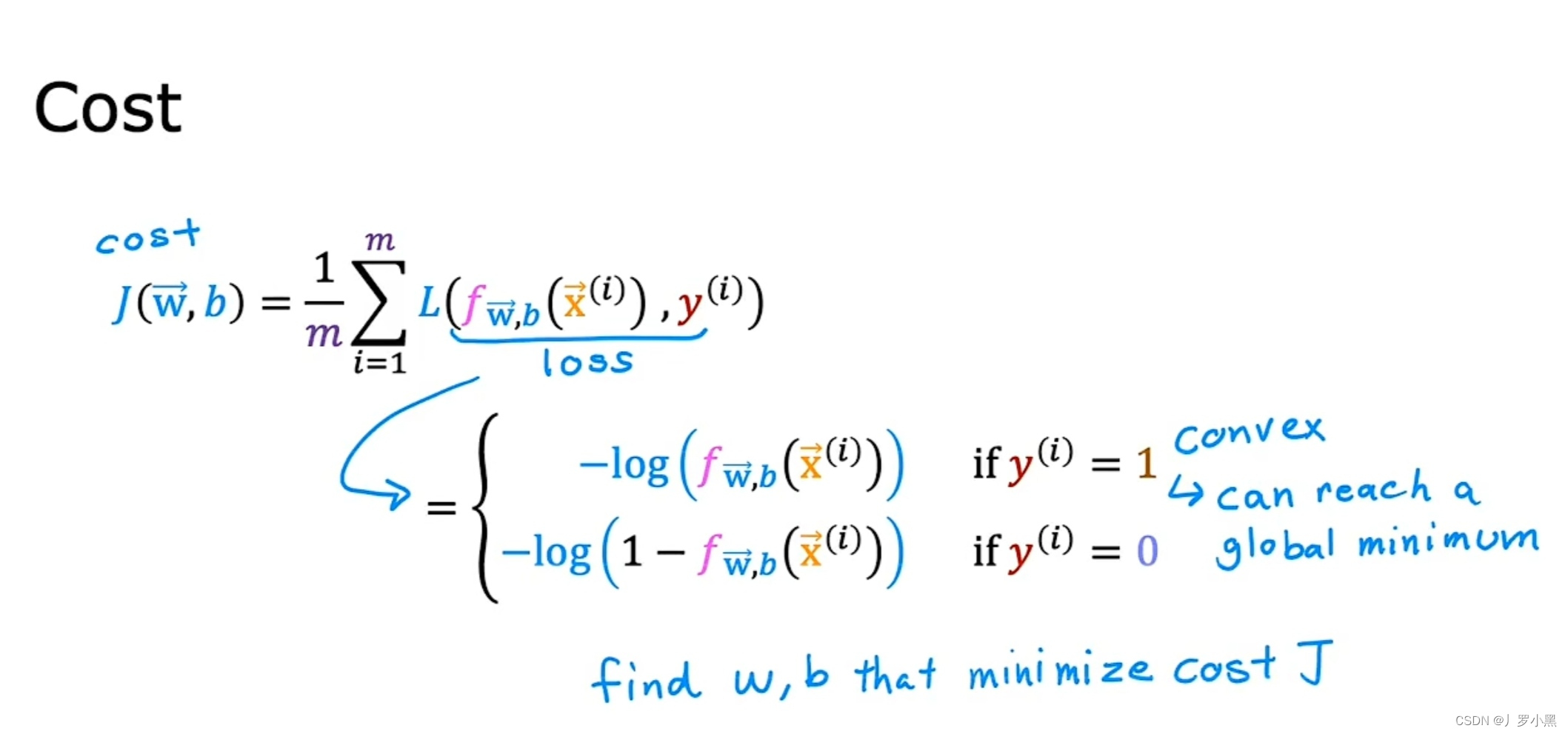文章目录
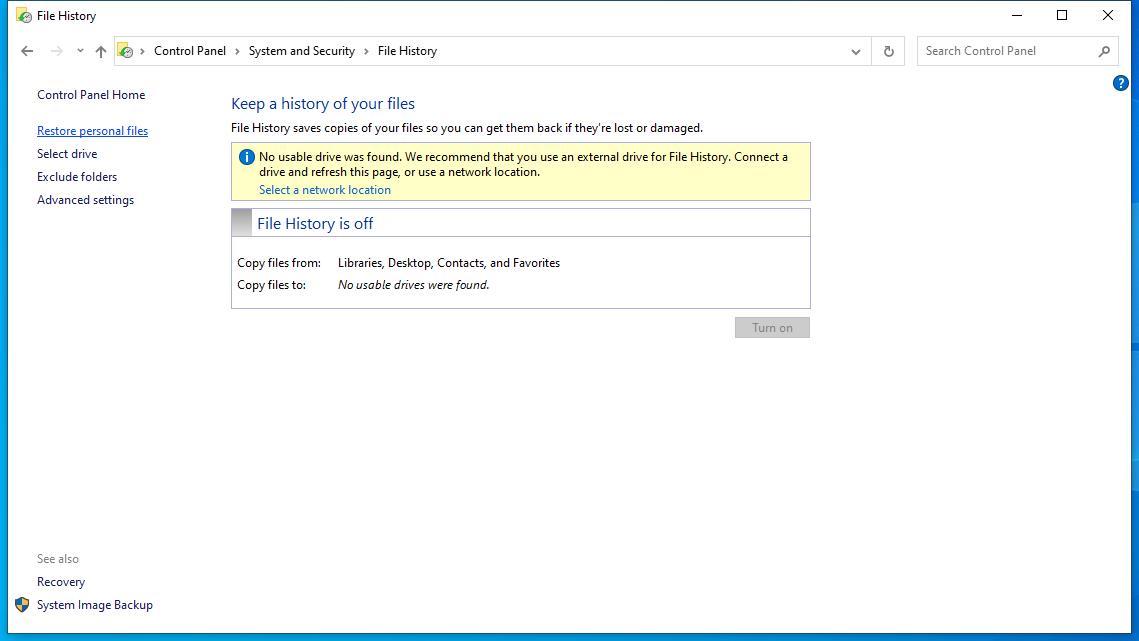
- 桶排序介绍
- 桶排序实现
- 桶排序复杂度和稳定性
- 桶排序复杂度
- 桶排序稳定性
- 代码实现
- 核心&总结
桶排序介绍
假设待排序的数组a中共有N个整数,并且已知数组a中数据的范围[0, MAX)。在桶排序时,创建容量为MAX的桶数组r,并将桶数组元素都初始化为0;将容量为MAX的桶数组中的每一个单元都看作一个"桶"。
在排序时,逐个遍历数组a,将数组a的值,作为"桶数组r"的下标。当a中数据被读取时,就将桶的值加1。例如,读取到数组a[3]=5,则将r[5]的值+1。
桶排序实现
假设a={8,2,3,4,3,6,6,3,9}, max=10。此时,将数组a的所有数据都放到需要为0-9的桶中。如下图:
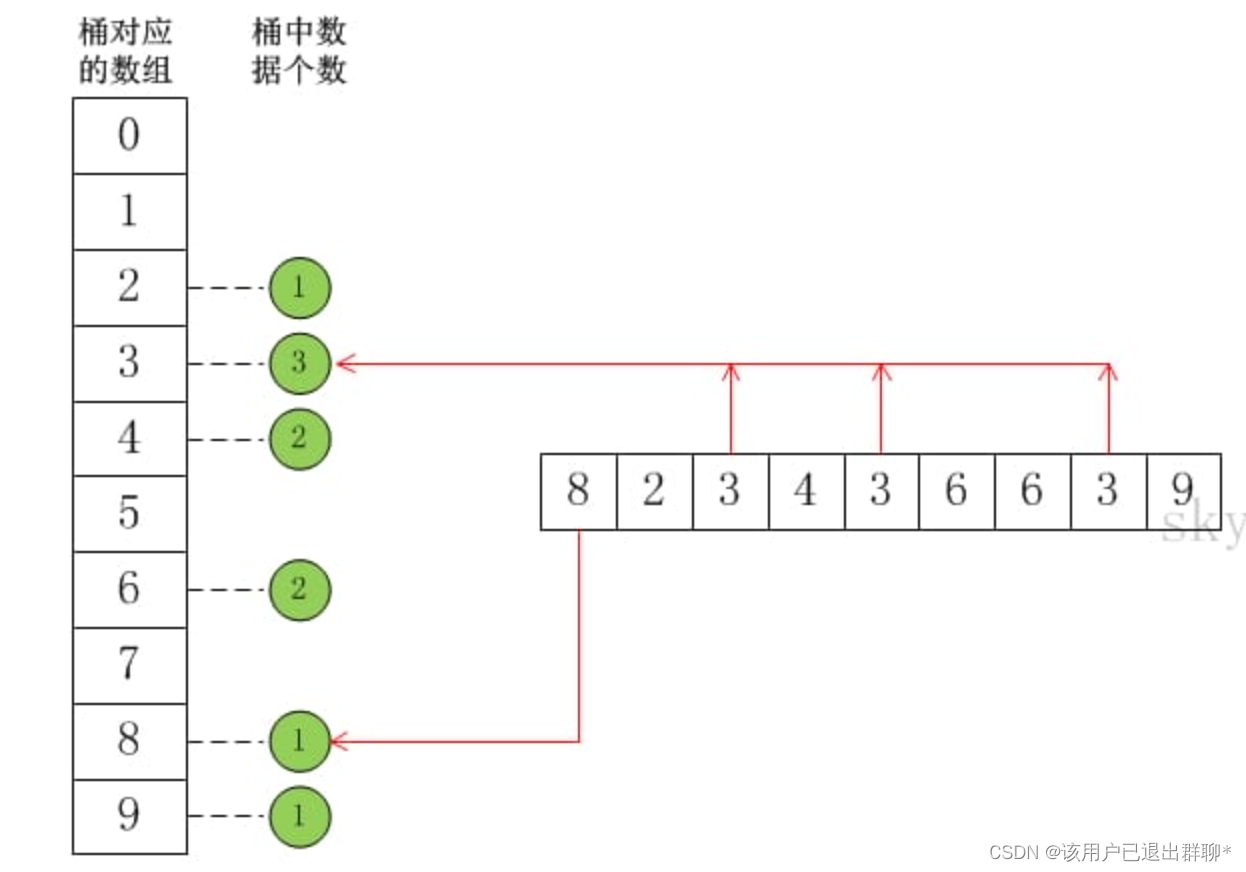
在将数据放到桶中之后,再通过一定的算法,将桶中的数据提出出来并转换成有序数组。就得到我们想要的结果了。
桶排序复杂度和稳定性
桶排序复杂度
- 平均时间复杂度: O(n + k)
- 最佳时间复杂度: O(n + k)
- 最差时间复杂度: O(n ^ 2)
- 空间复杂度: O(n * k)
桶排序最好情况下使用线性时间O(n),桶排序的时间复杂度,取决与对各个桶之间数据进行排序的时间复杂度,因为其它部分的时间复杂度都为O(n)。很显然,桶划分的越小,各个桶之间的数据越少,排序所用的时间也会越少。但相应的空间消耗就会增大。
桶排序稳定性
稳定性: 稳定
代码实现
package com.zxn;
/**
* @author zxn
* @ClassName BucketSort
* @Description
* @createTime 2023年05月05日 08:12:00
*/
public class BucketSort {
/*
* 桶排序
*
* 参数说明:
* a -- 待排序数组
* max -- 数组a中最大值的范围
*/
public static void bucketSort(int[] a, int max) {
int[] buckets;
if (a==null || max<1)
return ;
// 创建一个容量为max的数组buckets,并且将buckets中的所有数据都初始化为0。
buckets = new int[max];
// 1. 计数
for(int i = 0; i < a.length; i++) {
buckets[a[i]]++;
}
// 2. 排序
for (int i = 0, j = 0; i < max; i++) {
while( (buckets[i]--) >0 ) {
a[j++] = i;
}
}
buckets = null;
}
public static void main(String[] args) {
int i;
int a[] = {8,2,3,4,3,6,6,3,9};
System.out.printf("before sort:");
for (i=0; i<a.length; i++) {
System.out.printf("%d ", a[i]);
}
System.out.printf("\n");
bucketSort(a, 10); // 桶排序
System.out.printf("after sort:");
for (i=0; i<a.length; i++) {
System.out.printf("%d ", a[i]);
}
System.out.printf("\n");
}
}
核心&总结
- 要求被排序数组的元素必须全部为非负整数
- 数组最大值为桶的大小
- 数组元素的值为桶下标
- 桶元素为数组元素值的个数统计