作业调度问题是常见的线性规划(整数规划)问题,其中多个作业在多台机器上处理。每个作业由一系列任务组成,这些任务必须按给定的顺序执行,并且每个任务都必须在特定的机器上处理。如何有效的利用所有的机器在最短的时间内完成所有的作业任务,是摆在我们面前的一个大问题。
之前我们对or-tools官方提供的作业车间调度算法进行了分析,对作业车间调度问题还不是很了解的朋友请先查看我先前写的博客:
or-tools 整数规划案例分析:工作车间排班问题
定义需求
今天我们还是在此基础上给问题增加一些难度,我们的业务需求大致是这样的:
- 有多个【工单】
- 每一个【工单】都包含多个【工序】
- 每一个【工序】都包含多台允许加工的【设备】(也就是说【本工序】只允许在这些设备中 任选一台加工)
- 每一个【工序】都有一个加工的持续时间 例如2H
- 每台【设备】 都包含多段 维修时间 ,在【维修时间内】 【设备】是不允许加工的
- 最终的【目标】 最小化完成这些【工单下的工序】的总时间,并输出总时间、每个工序的加工【设备】号、每个工序的开始及结束时间。
为了便于在便于建模,我们把业务需求中的“工单”,“工序”,“设备”,“目标”等中文词汇改换成英文单词job,task,machine,objective,这样便于理解后面的代码逻辑:
- 有多个【job】
- 每一个【job】都包含多个【task】
- 每一个【task】都包含多台允许加工的【machine】(也就是说本【task】只允许在这些machine中 任选一台加工)
- 每一个【task】都有一个加工的持续时间 例如2H
- 每台【machine】 都包含多段 维修时间 在【维修时间内】 【machine】是不允许加工的
- 最终的【object】 最小化完成这些【job下的task】的总时间,并输出总时间,及每个【task】的加工machineid,以及每个【task】的开始及结束时间。
定义初始化变量
鉴于上述的业务需求,我们需要创建两个初始话变量Jobs和machine_maintenance_time,其中jobs变量包含了3个job,每个job又包含3个task,每个task又包含3个可选机器及其加工时间。jobs的结构正好符合业务需求中对工单结构的定义。machine_maintenance_time变量用来存储每台机器的维护时间段,每台机器可能会有1至2个时间段来进行维护。
import collections
from ortools.sat.python import cp_model
jobs = [ # task = (加工时间, 机器id)
[ # Job 0
[(3, 0), (1, 1), (5, 2)], # task0 有3个可选的加工设备
[(2, 0), (4, 1), (6, 2)], # task1 有3个可选的加工设备
[(2, 0), (3, 1), (1, 2)], # task2 有3个可选的加工设备
],
[ # Job 1
[(2, 0), (3, 1), (4, 2)],
[(1, 0), (5, 1), (4, 2)],
[(2, 0), (1, 1), (4, 2)],
],
[ # Job 2
[(2, 0), (1, 1), (4, 2)],
[(2, 0), (3, 1), (4, 2)],
[(3, 0), (1, 1), (5, 2)],
],
]
#机器维护时间
machine_maintenance_time=[
[(1,3),(6,8)],
[(0,2)],
[(1,3),(7,9)]
]需要说明的是这里的初始数据变量List或数组的下标都是从0开始,我们后续所说的第0个也就是实际第一个的意思。
这里的jobs是包含了多个job的List,每个job由3个task组成,而每个task里又有3个可选的加工设备,如:jobs[0][0][0]等于(3,0)表示在第0个机器上加工3个时间单位。task的格式为:task = (加工时间, 机器id)。这里我们需要搞清楚的是每个task都有3个可选的机器,并且必须任选其中一台机器进行加工。
machine_maintenance_time 是机器维护时间的初始数据,machine_maintenance_time是一个包含了3个元素的List,每一个元素代表了一台机器及其维护时间段,比如machine_maintenance_time[0]=[(1,3),(6,8)]表示第0台机器需要在1至3时刻和6至8时刻这两个时间段内进行维护,因此在这两个时段内是不允许加工的。以此类推这里我们记录了每一台设备需要维护的时间段,其中第0台和第2台设备各有2个时间段需要维护,第1台设备只有一个时间段需要维护。
接下来我们要创建cpmode模型然后定义一组工作变量:
- num_machines :机器数量。
- num_jobs:job的数量。
- horizon:完成所有job的理论最大时间。
- intervals_per_resources:该变量存储着每台机器上的所有间隔变量。
- starts: 该变量存放所有(job_id, task_id)的开始时间。
- presences:该变量存放所有(job_id, task_id, alt_id)对应的间隔变量是否有效的标志位。
model = cp_model.CpModel()
#定义机器数量变量
num_machines = len(machine_maintenance_time)
#定义job数量变量
num_jobs = len(jobs)
#定义完成所有job的理论最大时间
horizon = 0
for job in jobs:
for task in job:
max_task_duration = 0
for alternative in task:
max_task_duration = max(max_task_duration, alternative[0])
horizon += max_task_duration
machine_rest_time=0
for m in machine_maintenance_time:
for t in m:
horizon+=t[1]-t[0]
# 定义一组全局变量
intervals_per_resources = collections.defaultdict(list)
starts = {} # indexed by (job_id, task_id).
presences = {} # indexed by (job_id, task_id, alt_id).
job_ends = []这里需要说明的是horizon变量的值为每个job中的每个task中的最大完成时间的总和再加上所有机器的维护时间的总和。
添加约束条件
接下来我们需要为模型添加约束条件,由于我们的jobs是一个三重结构即job->task->alternatives,所以我们需要在遍历这个三重结构的过程中添加主要的约束条件,
# 遍历jobs,创建相关遍历,添加约束条件
for job_id in range(num_jobs):
job = jobs[job_id]
num_tasks = len(job)
previous_end = None
for task_id in range(num_tasks):
task = job[task_id]
min_duration = task[0][0]
max_duration = task[0][0]
num_alternatives = len(task)
all_alternatives = range(num_alternatives)
for alt_id in range(1, num_alternatives):
alt_duration = task[alt_id][0]
min_duration = min(min_duration, alt_duration)
max_duration = max(max_duration, alt_duration)
# 为每个task创建间隔变量
suffix_name = '_j%i_t%i' % (job_id, task_id)
start = model.NewIntVar(0, horizon, 'start' + suffix_name)
duration = model.NewIntVar(min_duration, max_duration,
'duration' + suffix_name)
end = model.NewIntVar(0, horizon, 'end' + suffix_name)
interval = model.NewIntervalVar(start, duration, end,
'interval' + suffix_name)
# 存储每个(job_id, task_id)的开始时间
starts[(job_id, task_id)] = start
# 添加任务的先后顺序约束
if previous_end is not None:
model.Add(start >= previous_end)
previous_end = end
# 为每个task的可选择的机器创建间隔变量
if num_alternatives > 1:
l_presences = []
for alt_id in all_alternatives:
alt_suffix = '_j%i_t%i_a%i' % (job_id, task_id, alt_id)
l_presence = model.NewBoolVar('presence' + alt_suffix)
l_start = model.NewIntVar(0, horizon, 'start' + alt_suffix)
l_duration = task[alt_id][0]
l_end = model.NewIntVar(0, horizon, 'end' + alt_suffix)
l_interval = model.NewOptionalIntervalVar(
l_start, l_duration, l_end, l_presence,
'interval' + alt_suffix)
l_presences.append(l_presence)
#强且仅当间隔变量的标志位为True时对start,duration,end进行赋值
model.Add(start == l_start).OnlyEnforceIf(l_presence)
model.Add(duration == l_duration).OnlyEnforceIf(l_presence)
model.Add(end == l_end).OnlyEnforceIf(l_presence)
# 添加每台机器上的所有间隔变量
intervals_per_resources[task[alt_id][1]].append(l_interval)
# 存放每个间隔变量是否有效的标志位
presences[(job_id, task_id, alt_id)] = l_presence
# 每个task任选一台机器的约束
model.AddExactlyOne(l_presences)
else:
intervals_per_resources[task[0][1]].append(interval)
presences[(job_id, task_id, 0)] = model.NewConstant(1)
job_ends.append(previous_end)
# 添加机器的约束.
for machine_id in range(num_machines):
#添加机器维护时间的约束
for t in machine_maintenance_time[machine_id]:
maintenance_interval=model.NewIntervalVar(t[0],t[1]-t[0],t[1], 'maintenance_time')
intervals_per_resources[machine_id].append(maintenance_interval)
#添加每台机器上的间隔变量不重叠的约束
intervals = intervals_per_resources[machine_id]
if len(intervals) > 1:
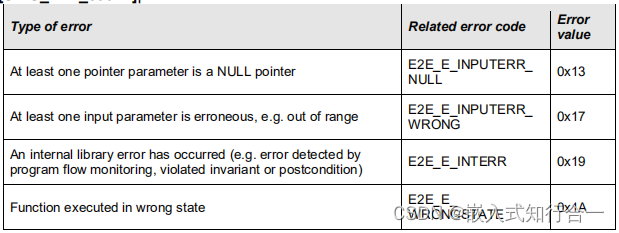
model.AddNoOverlap(intervals)这里我们需要说明的是在实现:"每个task可以在三台机器中任选一台进行加工的约束条件时",我们创建的是NewOptionalIntervalVar间隔变量,该变量与NewIntervalVar变量的差异是多了一个是否有效的标志位is_present ,根据官方文档的说明只有当is_present 为True时该间隔变量才是有效的,否则是无效的:
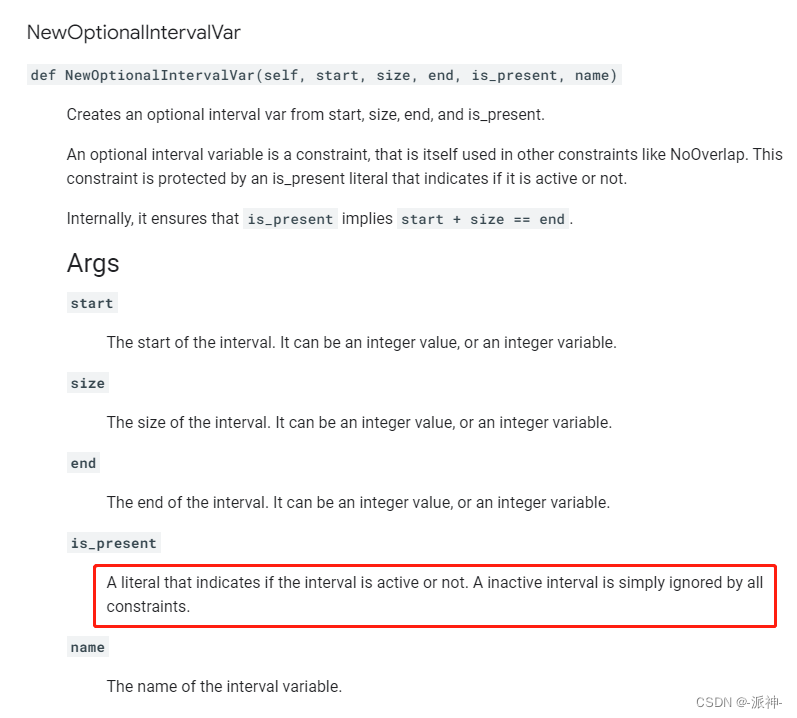
这里我们还用到了 OnlyEnforceIf 方法,它的是“当且仅当”的意思,因为我们要记录每个task选择的那台机器的start,duration,end,因此在可选的3台机器的3个间隔变量中,只允许一台机器的间隔变量的is_present标志位为True,所以OnlyEnforceIf可以强制让is_present为True的那台机器的start,duration,end值被记录下来。
我们在实现3台中任选一台的约束时使用了AddExactlyOne方法,该方法相当于以前的model.Add(sum([x,x,x,x])==1) ,即只允许一个数组变量中只能存在1个1,其它元素必须都是0。这样就可以保证3台中任选一台效果。
在添加机器维护时间的约束时,我们往intervals_per_resources变量中添加了每台机器维护时间的间隔变量,intervals_per_resources变量本来存储的是每台机器上所有task的间隔变量,我们在此基础上又为每台机器添加了维护时间的间隔变量,然后使用AddNoOverlap方法来确保每台机器上的间隔变量不会出现时间重叠的情况,这样就确保了再每台机器在维护时间内不会被任何一个task的占用。
设定优化目标
我们的优化目标为最小化完成所有job的时间,不过我们首先需要找到完成所有job的最大结束时间(通过AddMaxEquality来实现),然后再让这个最大时间最小化,就可以实现我们的优化目标了。
# 设定优化目标为:完成所有job的时间最短
makespan = model.NewIntVar(0, horizon, 'makespan')
model.AddMaxEquality(makespan, job_ends)
model.Minimize(makespan)模型求解
我们打印出所有job的task在每台机器上的开始时间start,持续时间duration,以及每个task所选的是3台机器中的哪一台。
# Solve model.
solver = cp_model.CpSolver()
solution_printer = SolutionPrinter()
status = solver.Solve(model, solution_printer)
# Print final solution.
for job_id in range(num_jobs):
print('Job %i:' % job_id)
for task_id in range(len(jobs[job_id])):
start_value = solver.Value(starts[(job_id, task_id)])
machine = -1
duration = -1
selected = -1
for alt_id in range(len(jobs[job_id][task_id])):
if solver.Value(presences[(job_id, task_id, alt_id)]):
duration = jobs[job_id][task_id][alt_id][0]
machine = jobs[job_id][task_id][alt_id][1]
selected = alt_id
print(
' task_%i_%i starts at %i (alt %i, machine %i, duration %i)' %
(job_id, task_id, start_value, selected, machine, duration))
print('Solve status: %s' % solver.StatusName(status))
print('Optimal objective value: %i' % solver.ObjectiveValue())
print('Statistics')
print(' - conflicts : %i' % solver.NumConflicts())
print(' - branches : %i' % solver.NumBranches())
print(' - wall time : %f s' % solver.WallTime())
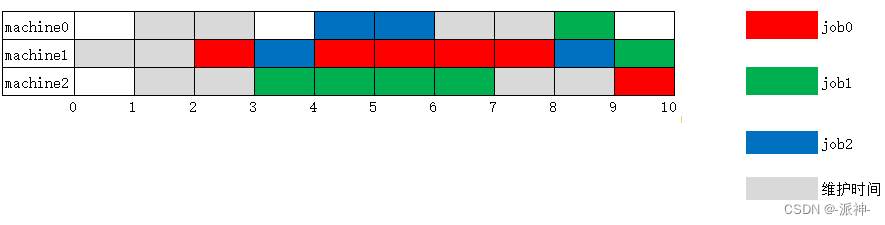
这里我们可以清楚的看到,每台机器的维护时间都没有被task占用,而且我们还得到的完成所有job的最短时间为10,以及模型的解为最优解: OPTIMAL, 不过这只是一个简单的例子,因为我们所使用的是最简单的初始化数据,然而在正式的商业项目中,我们往往很难获得最优解,一般情况下我们只能获得一个可行解。是否能获得最优解这取决于业务的复杂程度和机器的硬件资源尤其是cpu的内核数量及其频率等指标。
参考资料
or-tools官方文档