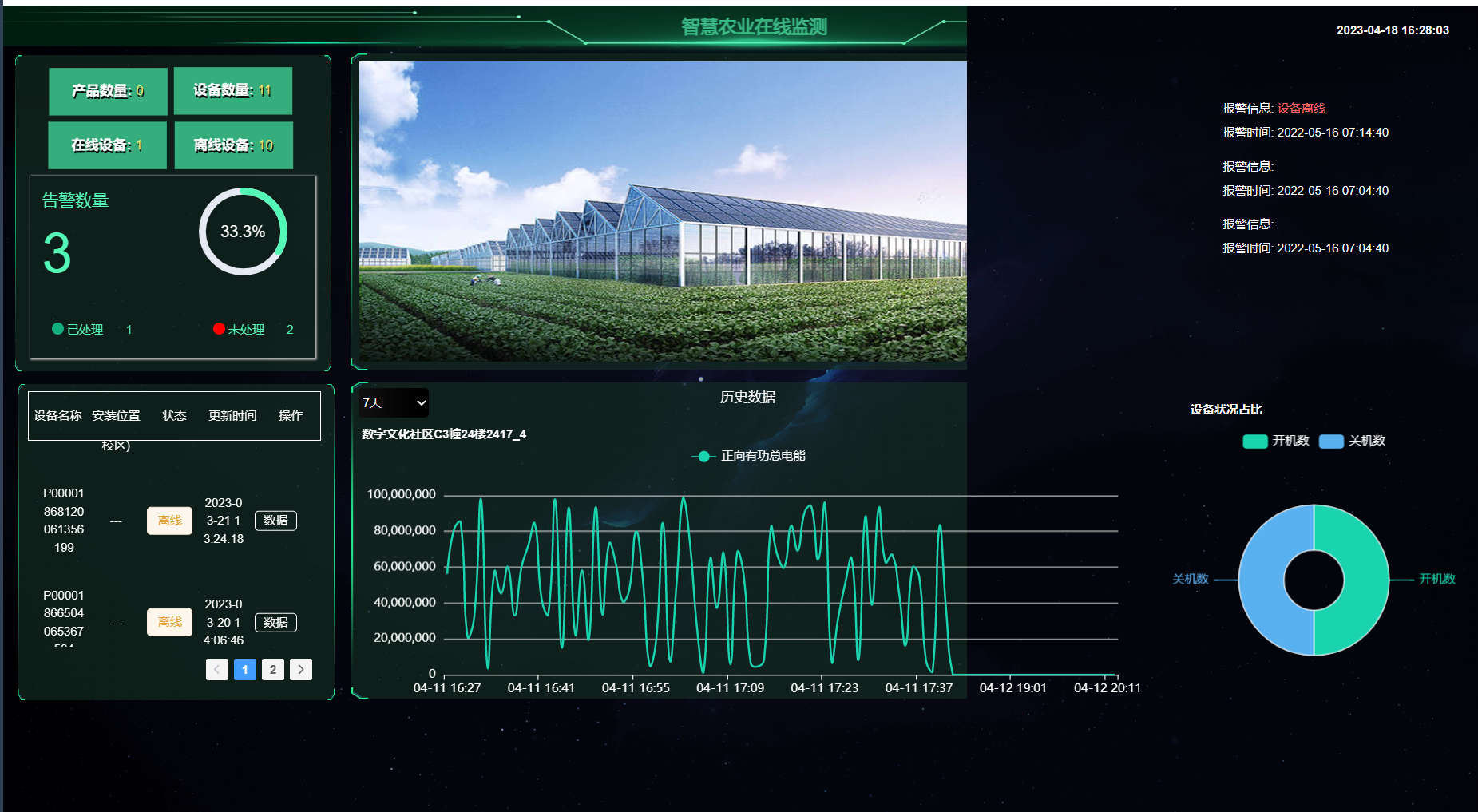
- 逻辑回归模型的预测过程
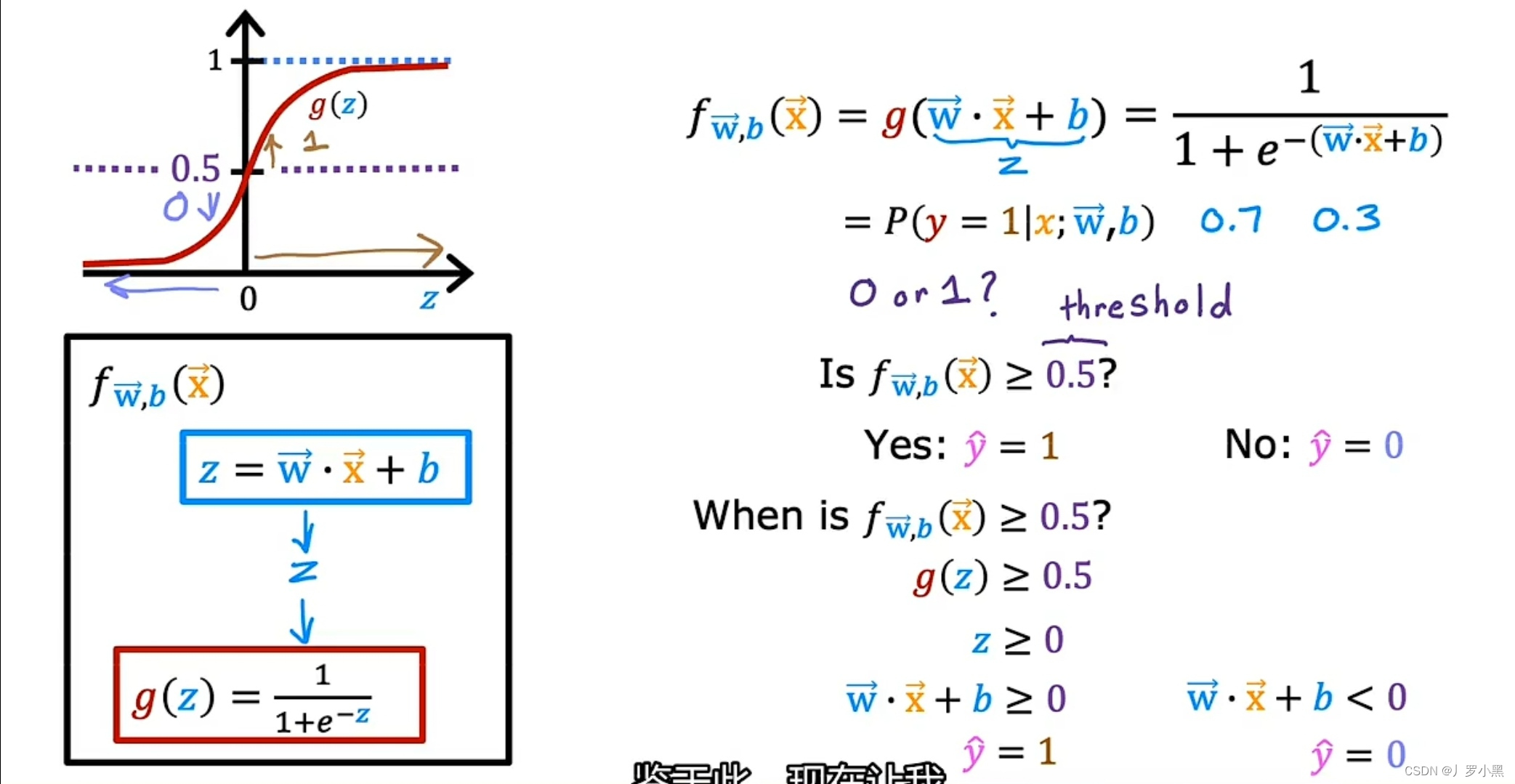
- 通常来说,我们先选择一个阈值0.5,当f(x) >= 0.5时,则预测y为1,当f(x)<0.5时,则预测y为0。
- 由此我们可以得出,当阈值取0.5时,g(z)取0.5,z取0。所以,向量W·向量X + b 取0
- 决策边界
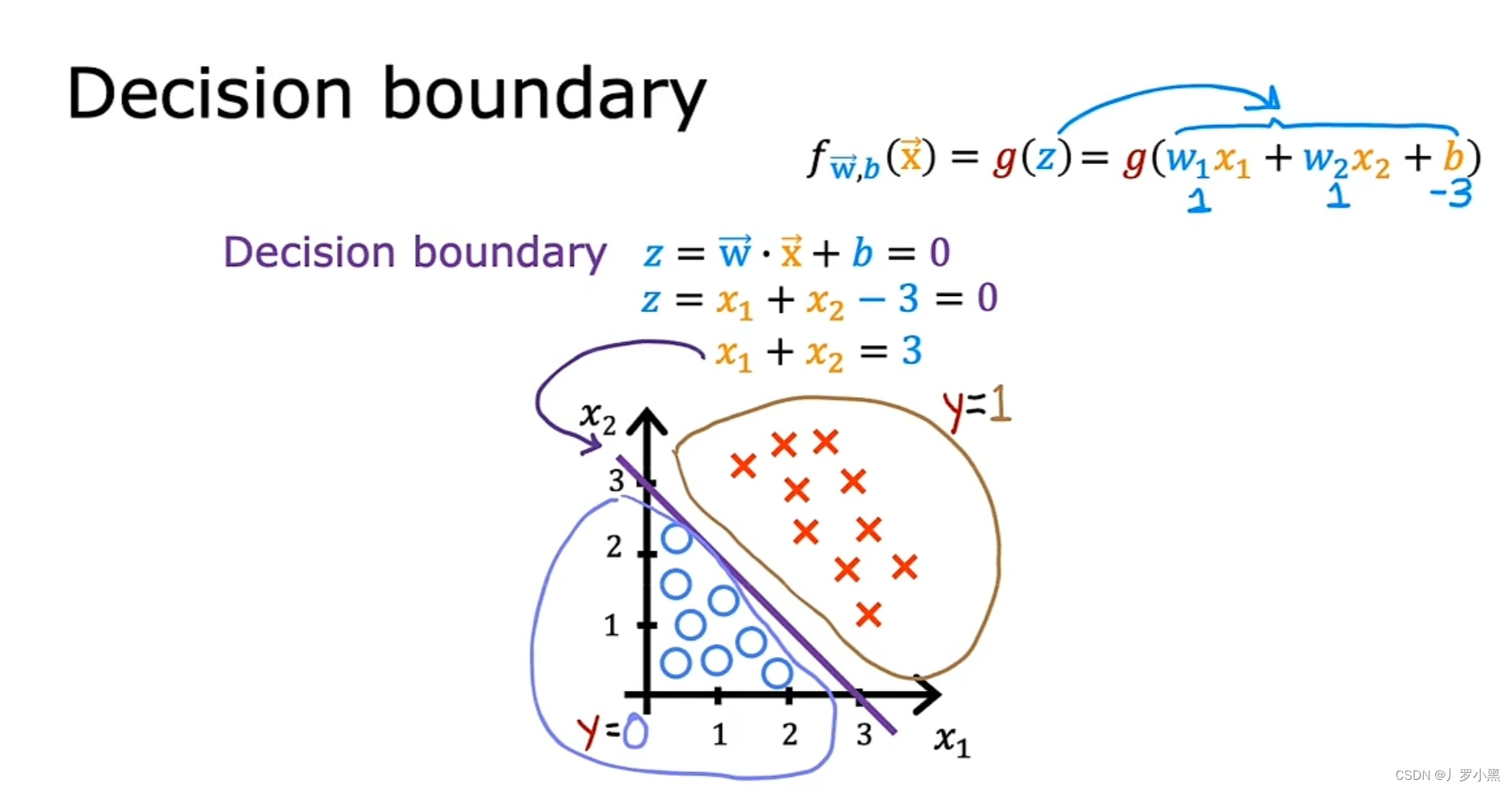
- 当W₁取1,W₂取1,b取-3时,z=0可以写成 X₁ +X₂ = 3,而这条直线就称为决策边界。
- 决策边界取决于逻辑回归函数的参数,而不是数据集


- 决策边界可以用于非线性函数图像,等复杂图像,来判断非常复杂形状的边界。
- 至于边界内部取0还是1,取决于我们自己如何定义,可以有点随意
- 逻辑回归模型中的成本函数

- 线性回归可以采用平方误差成本函数,得到的图像是凸函数,此时采用梯度下降算法可以得出成本函数的全局最小值。但,逻辑回归若也采用平方误差成本函数,得到的图像是非凸函数,此时采用梯度下降算法,只能得到局部最小值,很难得到全局最小值
- 通常,我们使用损失函数来作为逻辑回归的成本函数
- 因为,标签y的实际值为0或1,所以我们分类讨论
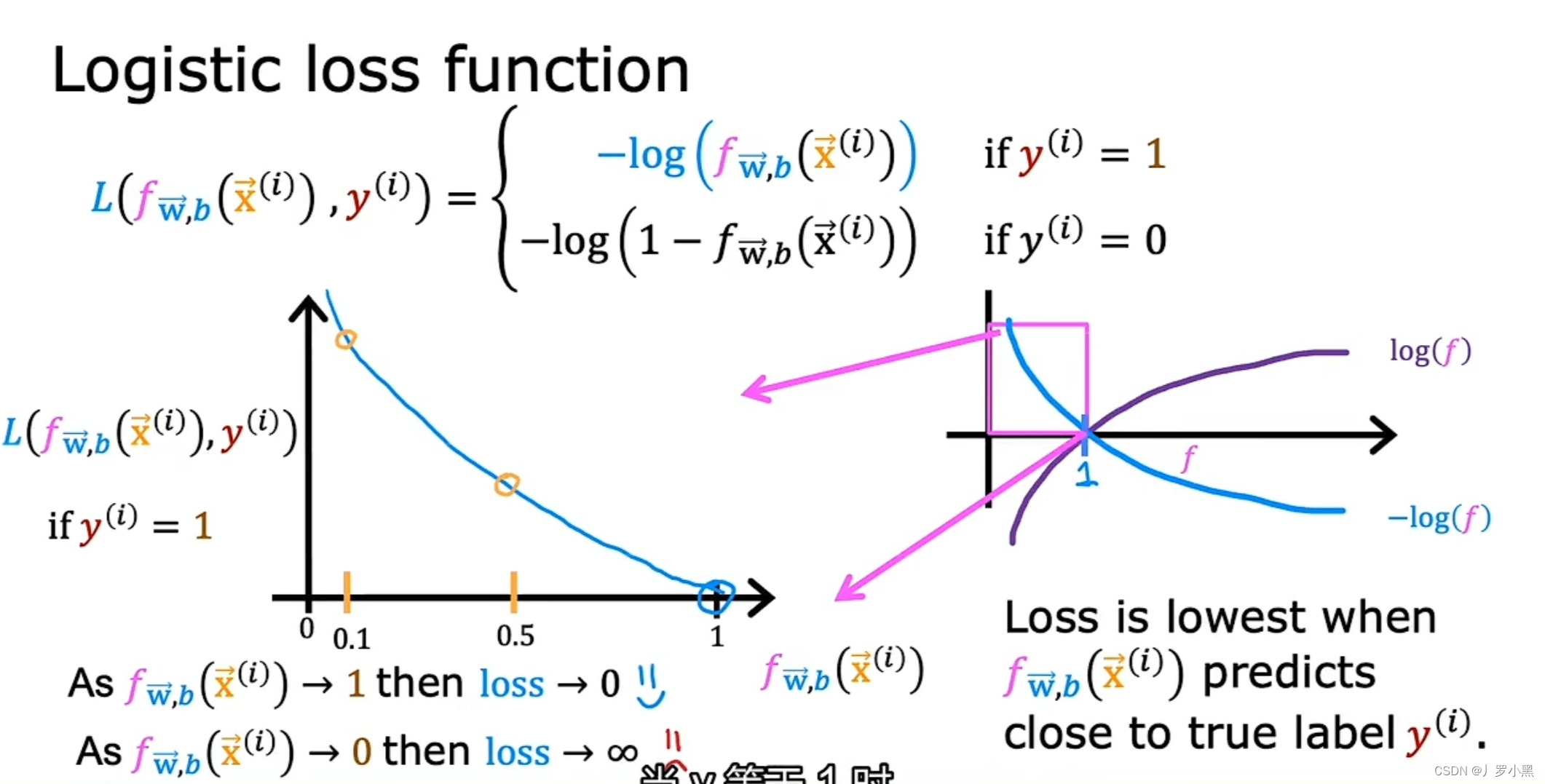
- 当标签y的实际值为1时,若f(x)为0.7,预测有0.7的可能性为1,实际就是1,则损失很小。若f(x)为0.1,预测有0.1的可能性为1,但实际就是1,则损失很大。
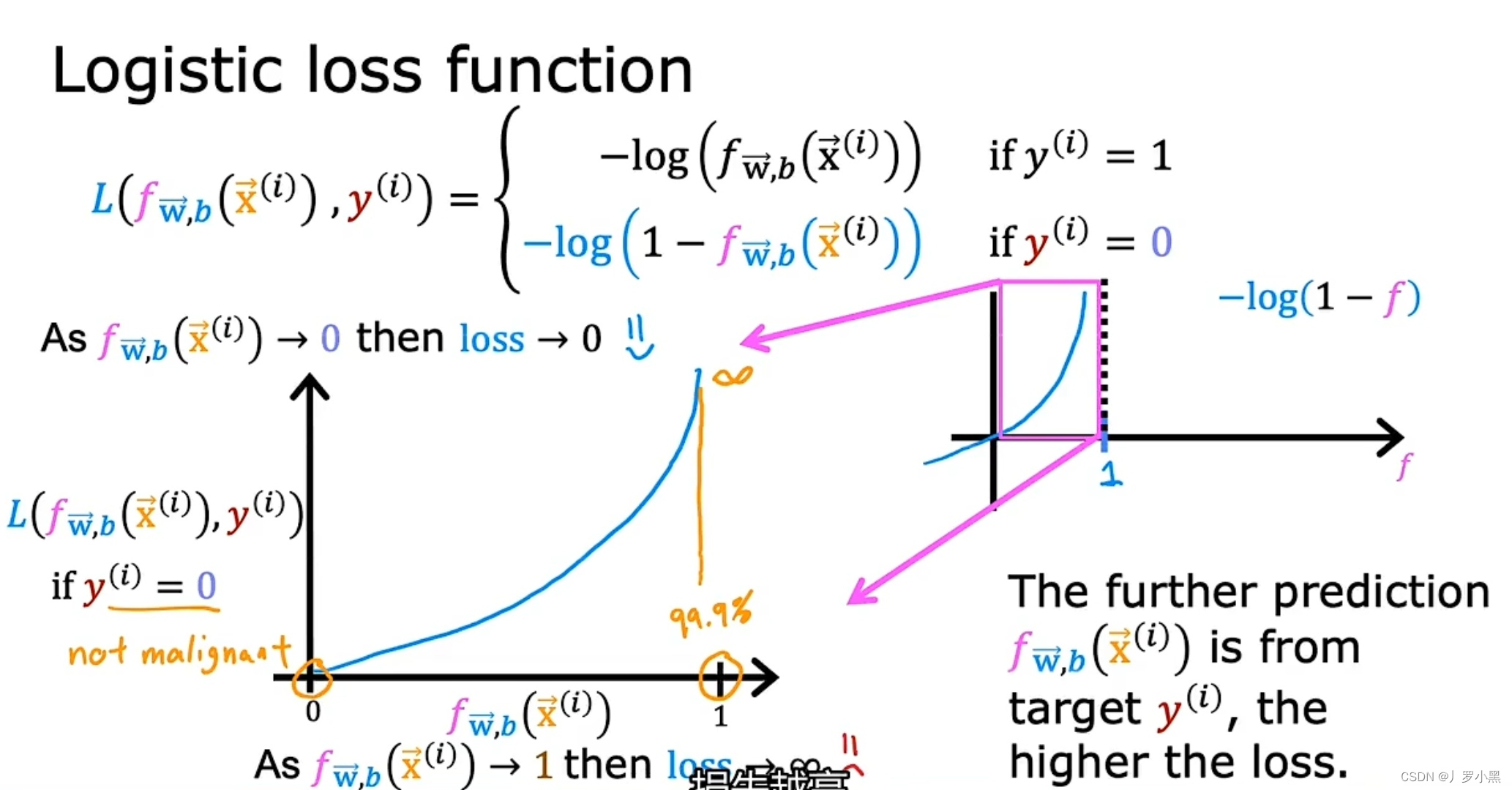
- 当标签y的实际值为0时,若f(x)为0.9,预测有0.9的可能性为1,但实际就是0,则损失很大。若f(x)为0.1,预测有0.1的可能性为1,实际就是0,则损失很小
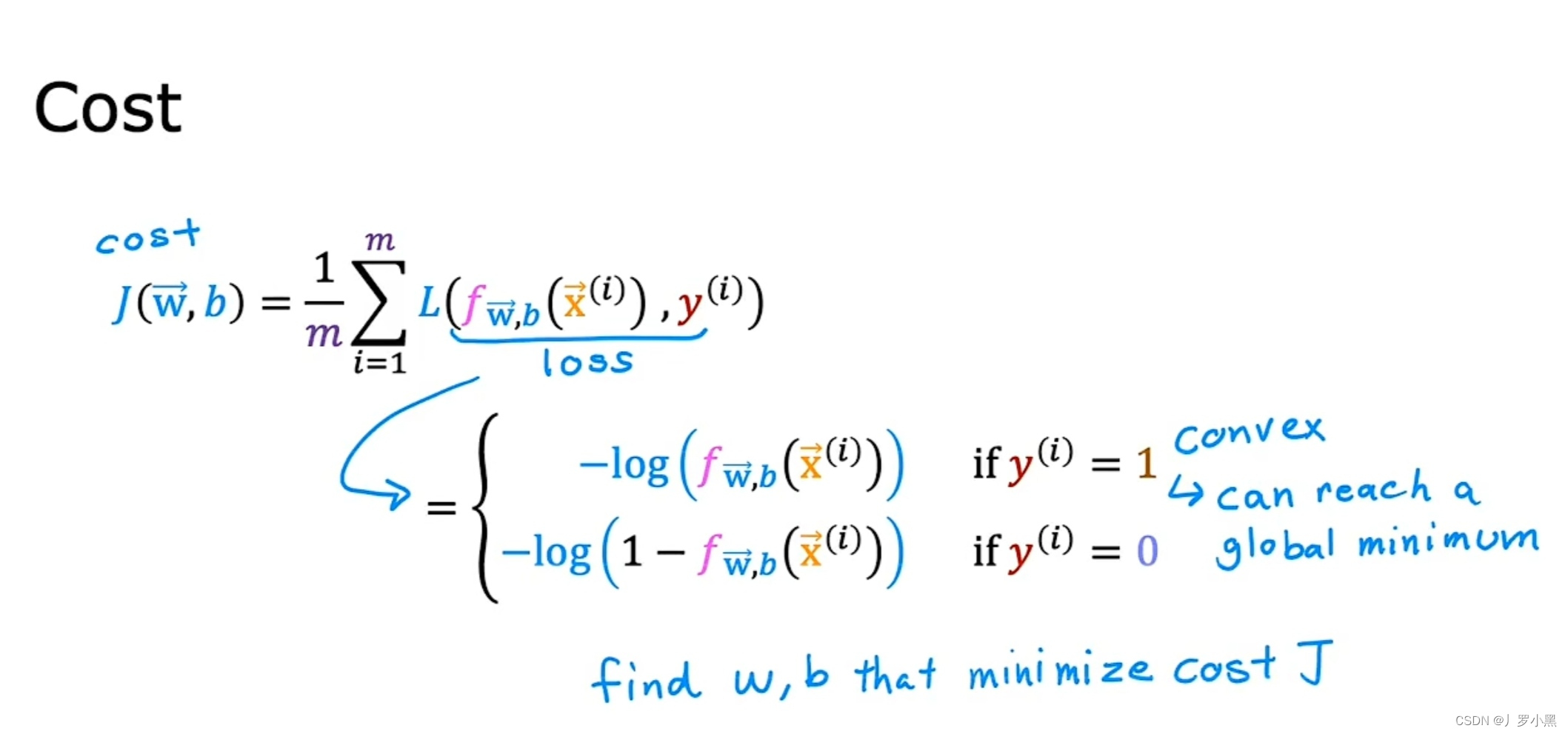
- 综上,我们使用损失函数来作为逻辑回归模型的成本函数,方便我们后续使用梯度下降算法来求全局最小值时的参数w,b




![windows下Ubuntu保姆级安装教程 [附VMware资源]](https://img-blog.csdnimg.cn/45d82d890f154f76b51780f8d6524666.png)