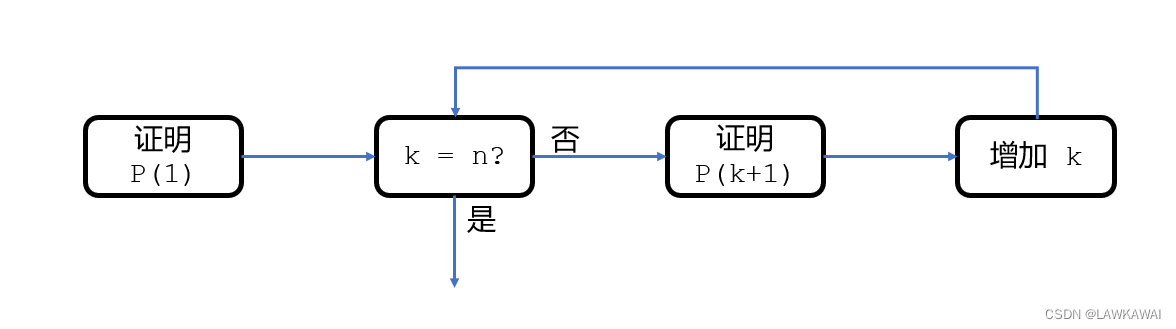
数学归纳法

• step1: 验证P(1)成立
• step2: 证明如果P(k)成立，那么P(k+1)也成立
• step3: 联合step1和step2，证明由P(1)->P(n)成立

例1：

证明：$1+3+...+(2n-1)=n^2$

1. 证明P(1)成立：$P(1)=1=1^2$成立
2. 假设$P(n-1)=(n-1{)}^2$,
   有：$P(n)=(n-1{)}^2+(2n-1)=n^2-2n+1+(2n-1)=n^2$
3. 证毕

数学归纳法在程序设计中有什么作用？

例2：

如下程序的正确性

int main()
{
    int sum = 0;
    for (int i = 1; i <= 100; i++)
    {
        sum += i;
    }
    std::cout << sum << std::endl;
    std::cin.get();
}

1. 证明 $P(1)$ 成立：在程序中就是变量的初始化。
2. 证明如果P(k)成立，那么P(k+1)也成立：未加i之前的sum是P(k), 加了i之后的sum未P(k+1)
3. 联合step1和step2，证明由$P(1)\to P(n)$成立: P(n)成立

递归函数设计的三个重要部分

1. 重要： 给【递归函数】一个明确的语义
2. 实现边界条件时的程序逻辑
3. 假设递归函数调用返回结果是正确的，实现本层函数逻辑

例3：递归求阶乘

1. 重要： 给【递归函数】一个明确的语义：
   f(n)代表n的阶乘， $f(n)=n!$
2. 实现边界条件时的程序逻辑:
   $n==1时，f(1)=1$
3. 假设递归函数调用返回结果是正确的，实现本层函数逻辑:
   $利用f(n-1)的值，计算f(n)=f(n-1)\ast n$

 int f(n)
 {
     if (n == 1) return 1;
     return f(n-1) * n;
 }

题目讲解

HZOJ-184-路飞吃桃

题目描述

路飞买了一堆桃子不知道个数，第一天吃了一半的桃子，还不过瘾，又多吃了一个。以后他每天吃剩下的桃子的一半还多一个，到 n 天只剩下一个桃子了。路飞想知道一开始买了多少桃子。

输入

输入一个整数 n(2≤n≤30)n(2≤n≤30)。

输出

输出买的桃子的数量。

样例输入1

2

样例输出1

4 = 2*(1+1)

样例输入2

3

样例输出2

10 = 2*(2*(1+1)+1)

数据规模与限定

时间限制：1 s

内存限制：64 M

题目解析

给定路飞吃了n天桃子，求原本桃子的数量

1. 重要： 给【递归函数】一个明确的语义：
   f(n)代表能吃n天的桃子的数量
2. 实现边界条件时的程序逻辑:
   $n==1时，f(1)=1$
3. 假设递归函数调用返回结果是正确的，实现本层函数逻辑:
   $利用f(n-1)的值，计算f(n)=(f(n-1)+1)\ast 2$

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <queue>
#include <stack>
#include <algorithm>
#include <string>
#include <map>
#include <set>
#include <vector>
using namespace std;

int f(int n)
{
	if (n == 1) return 1;
	return (f(n - 1) + 1) * 2;
}

int main()
{
	int n;
	cin >> n;
	cout << f(n) << endl;
	
	return 0;
}

HZOJ-186-弹簧版

题目描述

有一个小球掉落在一串连续的弹簧板上，小球落到某一个弹簧板后，会被弹到某一个地点，直到小球被弹到弹簧板以外的地方。

假设有 n个连续的弹簧板，每个弹簧板占一个单位距离，a[i]代表代表第 i个弹簧板会把小球向前弹 a[i]个距离。比如位置 1 的弹簧能让小球前进 2 个距离到达位置 3 。如果小球落到某个弹簧板后，经过一系列弹跳会被弹出弹簧板，那么小球就能从这个弹簧板弹出来。

现在小球掉到了1 号弹簧板上面，那么这个小球会被弹起多少次，才会弹出弹簧板。 1号弹簧板也算一次。

输入

第一个行输入一个 n代表一共有 n(1≤n≤100000)n(1≤n≤100000)个弹簧板。

第二行输入 n​​ 个数字，中间用空格分开。第 i​个数字$a[i](0<a[i]\le 30)$代表第 i​个弹簧板可以让小球移动的距离。

输出

输出一个整数，表示小球被弹起的次数。

样例输入1

5
2 2 3 1 2

样例输出1

2

样例输入2

5
1 2 3 1 2

样例输出2

4

数据规模与限定

时间限制：1 s

内存限制：64 M

题目解析

1. 重要： 给【递归函数】一个明确的语义：
   f(i)代表小球从i位置开始，被弹出弹簧版的次数
2. 实现边界条件时的程序逻辑:
   $i>=n时，f(i)=0$
3. 假设递归函数调用返回结果是正确的，实现本层函数逻辑:
   $利用f(i+a[i])的值，计算f(i)=f(i+a[i])+1$

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <queue>
#include <stack>
#include <algorithm>
#include <string>
#include <map>
#include <set>
#include <vector>
using namespace std;

int f(int i, vector<int>& arr, int n)
{
	if (i >= n) return 0;
	return f(i + arr[i], arr, n) + 1;
}

int main()
{
	int n;
	cin >> n;
	vector<int> arr;   // 读入一个数组
	for (int i = 0, a; i < n; i++)
	{
	    cin >> a;
	    arr.push_back(a);
	}
	cout << f(0, arr, n) << endl;
	
	return 0;
}

HZOJ-235-递归实现指数型枚举

题目描述

​ 从 1−n 这 n 个整数中随机选取任意多个，每种方案里的数从小到大排列，按字典序输出所有可能的选择方案。
指数型枚举：最多枚举n个，并且每一个数字都要大于它前面的数字。
字典序输出：从小到大输出。

输入

​ 输入一个整数 n。（1≤n≤10）

输出

​ 每行一组方案，每组方案中两个数之间用空格分隔。

​ 注意每行最后一个数后没有空格。

样例输入

3

样例输出

1
1 2
1 2 3
1 3
2
2 3
3

样例输入2

4

样例输出2

1
1 2
1 2 3
1 2 3 4
1 2 4
1 3
1 3 4
1 4
2
2 3
2 3 4
2 4
3
3 4
4

数据规模与约定

​ 时间限制：1 s

​ 内存限制：256 M

​ 100% 的数据保证 1≤n≤10

题目解析

三个小问题需要解决：

• 如何按照字典序输出? 可以想象成为现在有n个格子需要去填，每个位置都是从小到大去枚举，枚举顺序就是字典序顺序。

• 如何保证每个位置的数字都大于前面的数字？ 在枚举过程中，传入一个变量，这个变量标记了当前位置最小可以取的数字是多少。

• 如何输出这些结果？

1. 重要： 给【递归函数】一个明确的语义：
   $i$ 代表当前枚举的是第$i$个位置，$j$代表当前位置最小可以取的数字，n代表当前位置最大可以取的数字，则 $f(i,j,n)$代表从第$i$个位置开始向后枚举，并且第$i$个位置可以选择的最小的数字为$j$的情况下，可以实现的所有指数型枚举。
2. 实现边界条件时的程序逻辑:
   $j>n时，返回$
3. 假设递归函数调用返回结果是正确的，实现本层函数逻辑:
   $f(i,j,n)$是一个集合
   (1) 包含当前$i$位置的最小可以取的数字$j$+ 从$i+1$位置开始向后枚举，并且第$i+1$位置可以选择的最小数字为$j+1$的集合
   即$f(i,j,n)=j+f(i+1,j+1,n)$
   (2) 包含当前$i$位置的最小可以取的数字$j+1$+ 从$i+1$位置开始向后枚举，并且第$i+1$位置可以选择的最小数字为$j+2$的集合
   即$f(i,j,n)=j+1+f(i+1,j+2,n)$
   …
   $f(i,j,n)=n+f(i+1,n+1,n)$

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <queue>
#include <stack>
#include <algorithm>
#include <string>
#include <map>
#include <set>
#include <vector>
using namespace std;


int arr[10];  // 用来存储枚举的数字，最大个数为10

void print_one_result(int n)    // 将arr数组中当前枚举得到的结果进行输出
{
    for (int i = 0; i <= n; i++)
    {
        if (i) cout << " ";
        cout << arr[i]; 
    }
    cout << endl;
    return ;
}

void f(int i, int j, int n)
{
	if (j > n) return ;
	for (int k = j; k <= n; k++)
	{
	    arr[i] = k;
	    print_one_result(i);   // 输出当前位置i及之前所枚举的数字
	    f(i+1, k+1, n);
	}
	return ;
}


int main()
{
	int n;
	cin >> n;
	f(0, 1, n);   // 开始枚举，从0位置开始枚举，0位置可以填写的最小数字是1， 最大是n
	
	return 0;
}

HZOJ-236-递归实现组合型枚举

题目描述

​ 从 1−n这 n 个整数中随机选取 m 个，每种方案里的数从小到大排列，按字典序输出所有可能的选择方案。

输入

​ 输入两个整数 n,m。（1≤m≤n≤10）

输出

​ 每行一组方案，每组方案中两个数之间用空格分隔。

​ 注意每行最后一个数后没有空格。

样例输入

3 2

样例输出

1 2
1 3
2 3

样例输入2

5 3

样例输出2

1 2 3
1 2 4
1 2 5
1 3 4
1 3 5
1 4 5
2 3 4
2 3 5
2 4 5
3 4 5

数据规模与约定

​ 时间限制：1 s

​ 内存限制：256 M

​ 100% 的数据保证 1≤m≤n≤10

题目解析

三个小问题需要解决：

• 如何按照字典序输出? 可以想象成为现在有n个格子需要去填，每个位置都是从小到大去枚举，枚举顺序就是字典序顺序。

• 如何保证每个位置的数字都大于前面的数字？ 在枚举过程中，传入一个变量，这个变量标记了当前位置最小可以取的数字是多少。

• 如何输出这些结果？

1. 重要： 给【递归函数】一个明确的语义：
   $i$ 代表当前枚举的是第$i$个位置，$j$代表当前位置最小可以取的数字，n代表当前位置最大可以取的数字，m代表最多可以枚举多少位；则 $f(i,j,n,m)$代表从第$i$个位置开始向后枚举，并且第$i$个位置可以选择的最小的数字为$j$的情况下，可以实现的所有组合型枚举。
2. 实现边界条件时的程序逻辑:
   是否选择了足够多数量的数字， $i==m时，输出，返回$
3. 假设递归函数调用返回结果是正确的，实现本层函数逻辑:
   $f(i,j,n,m)$是一个集合
   (1) 包含当前$i$位置的最小可以取的数字$j$+ 从$i+1$位置开始向后枚举，并且第$i+1$位置可以选择的最小数字为$j+1$的集合
   即$f(i,j,n,m)=j+f(i+1,j+1,n,m)$
   (2) 包含当前$i$位置的最小可以取的数字$j+1$+ 从$i+1$位置开始向后枚举，并且第$i+1$位置可以选择的最小数字为$j+2$的集合
   即$f(i,j,n,m)=j+1+f(i+1,j+2,n,m)$
   …
   $f(i,j,n,m)=n+f(i+1,n+1,n,m)$

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <queue>
#include <stack>
#include <algorithm>
#include <string>
#include <map>
#include <set>
#include <vector>
using namespace std;


int arr[10];  // 用来存储枚举的数字，最大个数为10

void print_one_result(int m)    // 将arr数组中当前枚举得到的结果进行输出
{
	for (int i = 0; i < m; i++)
	{
		if (i) cout << " ";
		cout << arr[i];
	}
	cout << endl;
	return;
}

void f(int i, int j, int n, int m)
{
	if (i == m)
	{
		print_one_result(m);  // 枚举了m位，是时候输出这m个数字
		return ;               // 输出完结果后就可以返回
	}
	for (int k = j; k <= n && m - i - 1 <= n - k; k++)    // 开始枚举, 加了一个条件，实现剪枝，循环不需要
	{
		arr[i] = k;
		f(i + 1, k + 1, n, m);
	}
	return ;
}


int main()
{
	int n, m;
	cin >> n >> m;
	f(0, 1, n, m);   // 开始枚举，从0位置开始枚举，0位置可以填写的最小数字是1， 最大是n

	return 0;
}

HZOJ-237-递归实现排列型枚举

题目描述

​ 从 1−n这 n个整数排成一排并打乱次序，按字典序输出所有可能的选择方案。
输出全排列。
排列型枚举：后面的数字可以比前面的数字小，当前位置枚举的数字必须是前面位置没用过的数字。

输入

​ 输入一个整数 n。（1≤n≤8）

输出

​ 每行一组方案，每组方案中两个数之间用空格分隔。

​ 注意每行最后一个数后没有空格。

样例输入

3

样例输出

1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1

数据规模与约定

​ 时间限制：1 s

​ 内存限制：256 M

​ 100% 的数据保证 1≤n≤8

题目解析

三个小问题需要解决：

• 如何按照字典序输出? 可以想象成为现在有n个格子需要去填，每个位置都是从小到大去枚举，枚举顺序就是字典序顺序。

• 如何判断当前枚举的数字在之前有没有出现过？ 在枚举过程中，传入一个变量，这个变量标记了当前位置最小可以取的数字是多少。

• 如何输出这些结果？

1. 重要： 给【递归函数】一个明确的语义：
   $i$ 代表当前枚举的是第$i$个位置，n代表当前位置最大可以取的数字；则 $f(i,n)$代表从第$i$个位置开始向后枚举，枚举n位的全排列。
2. 实现边界条件时的程序逻辑:
   $i==n时，输出，返回$
3. 假设递归函数调用返回结果是正确的，实现本层函数逻辑:
   $f(i,n)$是一个集合
   (1) 包含当前$i$位置之前没有出现过的数字$v[0]$+ 从$i+1$位置开始向后枚举的全排列
   即$f(i,n)=v[0]+f(i+1,n)$
   (2) 包含当前$i$位置之前没有出现过的数字$v[1]$+ 从$i+1$位置开始向后枚举的全排列
   即$f(i,n)=v[1]+f(i+1,n)$
   …
   $f(i,n)=v[n-i]+f(i+1,n)$

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <queue>
#include <stack>
#include <algorithm>
#include <string>
#include <map>
#include <set>
#include <vector>
using namespace std;


int arr[10], vis[10] = {0};  // arr用来存储枚举的数字，最大个数为10; vis用来存储没有被使用过的数字

void print_one_result(int n)    // 将arr数组中当前枚举得到的结果进行输出
{
	for (int i = 0; i < n; i++)
	{
		if (i) cout << " ";
		cout << arr[i];
	}
	cout << endl;
	return;
}

void f(int i, int n)
{
	if (i == n)
	{
		print_one_result(n);  // 枚举了n位，是时候输出这n个数字
		return ;               // 输出完结果后就可以返回
	}
	for (int k = 1; k <= n; k++)    // 开始枚举, 加了一个条件，实现剪枝，循环不需要
	{
	    if (vis[k]) continue;   // 如果第k位置之前被使用过（vis[k] = 1），则直接跳过
		arr[i] = k;              // k没有被使用过, 把k放在第i位
		vis[k] = 1;              // 同时标记k这个数字已经被使用了
		f(i + 1, n);           // 此时，从第i+1位后面已经枚举完了，返回到当前这层的枚举，也就是说，已经输出了第i个位置等于k的所有结果
		vis[k] = 0;     // 对k进行回收，也就是可以对k重新使用
	}
	return ;
}


int main()
{
	int n;
	cin >> n;
	f(0, n);   // 开始枚举，从0位置开始枚举，n位全排列

	return 0;
}