租用游艇

1.格式化输入二维数组:1-2,1-3,1-4,2-3,2-4,3-4... ...
for(int i=1; i<=n-1; i++)
for(int j=i+1; j<=n; j++)2.三重for循环枚举路径:第一层for枚举1-k中转站,第二,三层为 i站点--j站点直达所需距离
3.输出1-n(a[1][n])的最短路径:有序!1-n ≠ n-1
#include<stdio.h>
#include<string.h>
int main()
{
int n,a[210][210];
scanf("%d",&n);
memset(a,1,sizeof(a)); //数组初值赋大数
for(int i=1; i<=n-1; i++) //注意输入格式
{
for(int j=i+1; j<=n; j++)
{
scanf("%d",&a[i][j]);
}
}
for(int k=1; k<=n; k++) //枚举1-k中转站
{
for(int i=1; i<=n; i++)
{
for(int j=1; j<=n; j++)
{
if(a[i][j]>a[i][k]+a[k][j])
{
a[i][j]=a[i][k]+a[k][j];
}
}
}
}
printf("%d",a[1][n]); //1-n的最短路径
}修路

1.变量设置:结构体存储:点1+点2+1到2的距离
2.初始化&&找find father:并查集基本操作
3.升序排序距离:调用库函数,快排不行
4.unionn时加入权值(距离):
5.终止条件:sum==n-1,线全部用完
6.注意:条件已知已连接点点,两点距离设为0即可
#include<bits/stdc++.h>
using namespace std;
int fa[500501];
long double ans=0.0;
int sum=0;
int k=0;
struct node
{
int x,y;
double z;
} a[500501];
void init(int n)
{
for(int i=1; i<=n; i++)
{
fa[i]=i;
}
}
int find(int i)
{
if(fa[i]==i) return i;
else
{
return find(fa[i]);
}
}
bool cmp(node a,node b)
{
return a.z<b.z;
}
void add(int i,int j,double l) //构造结构体存储两点间距离(点+点+距离)
{
a[++k].x=i;
a[k].y=j;
a[k].z=l;
}
int main()
{
int i,j,m,n,b,c;
int xx[500501],yy[500501];
scanf("%d %d",&n,&m);
init(n);
for(i=1; i<=n; i++)
{
scanf("%d %d",&xx[i],&yy[i]);
}
for(i=1; i<=n; i++)
for(j=i+1; j<=n; j++)
{
long double z=(double)sqrt((double)(xx[i]-xx[j])*(xx[i]-xx[j])+(double)(yy[i]-yy[j])*(yy[i]-yy[j]));
add(i,j,z);
}
for(i=1; i<=m; i++)
{
scanf("%d %d",&b,&c);
add(b,c,0.0);
}
//quick(1,k);
sort(a+1,a+1+k,cmp);
for(i=1; i<=k; i++)
{
int x=find(a[i].x);
int y=find(a[i].y);
if(x!=y)
{
fa[x]=y;
sum++; //线使用量+1
ans+=a[i].z; //权值求和
}
if(sum==n-1) break; //n为点个数,n-1为线个数
}
printf("%.2Lf",ans);
return 0;
}最小生成树
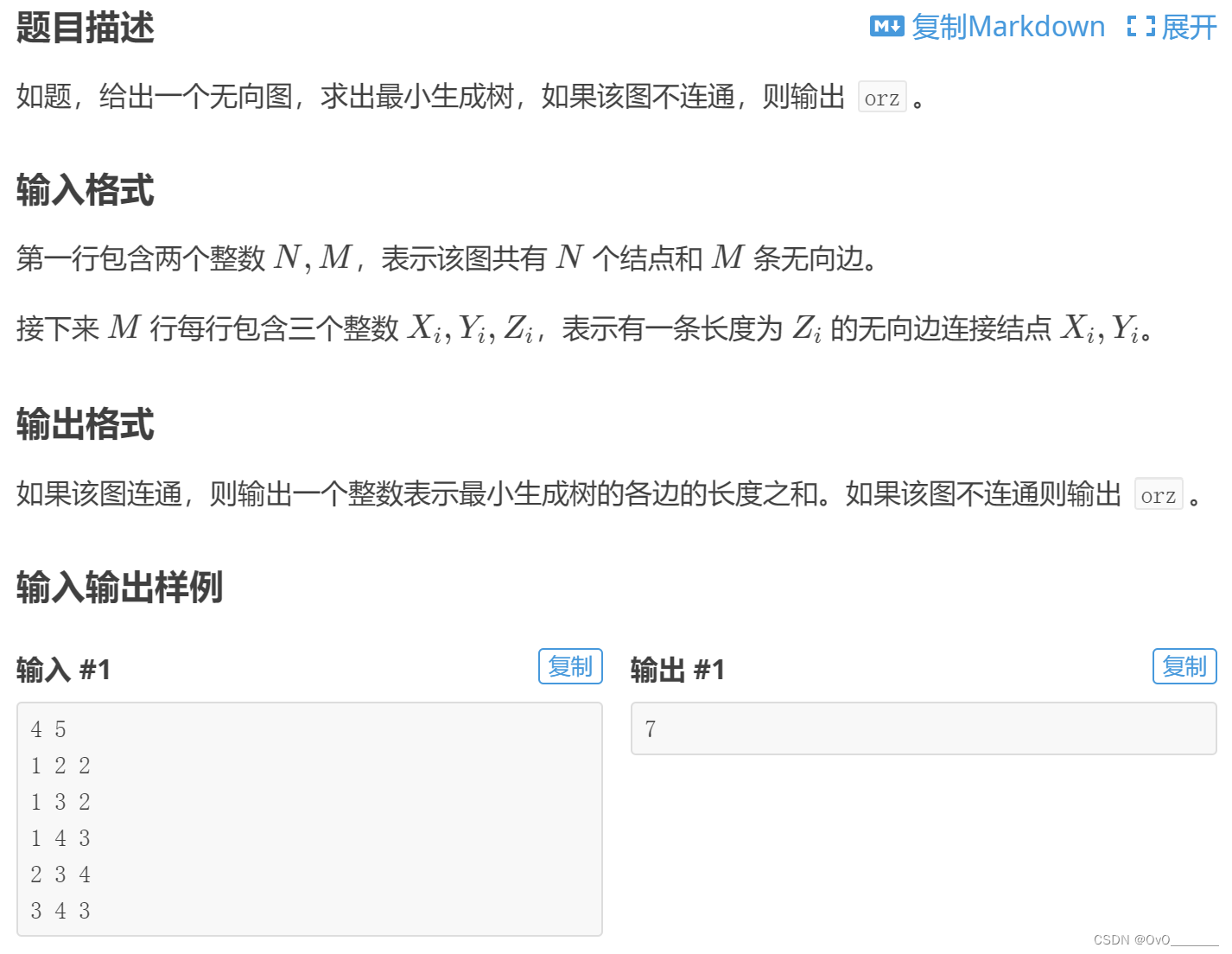
1.利用快排对边长短排序:从最小边开始连接
2.连接点点(集合):unionn并查集,fa相同continue,不同则合并,同时加上权值3.查找是否连通:即为察father是否唯一
4.注意:并查集标准操作,初始化+找find father+合并
#include<stdio.h>
int n,m;
int fa[210000];
long long ans=0;
int cnt=0;
struct node
{
int x,y,z;
} a[210000];
void quick(int left,int right)
{
int i,j; //双指针i,j
struct node t,temp; //最左边为基准数,每次递归过程数会变化
temp=a[left]; //结构体t,temp(需整体交换,排序过程)
i=left; //同理,变化数利用变量代用
j=right;
if(left>right) return ;
while(i!=j)
{
while(a[j].z>=temp.z&&i<j)
j--;
while(a[i].z<=temp.z&&i<j)
i++;
if(i<j) //i,j没有相遇时
{
t=a[i]; //整体交换
a[i]=a[j];
a[j]=t;
}
}
a[left]=a[i]; //将i,j相遇的值给队首
a[i]=temp; //此时基准数位于相遇点
quick(left,i-1);
quick(j+1,right);
}
void init(int n) //fa[]初始化
{
for(int i=1; i<=n; i++)
{
fa[i]=i;
}
}
int find(int i) //查询,找爸爸
{
if(i==fa[i]) return i;
else
{
fa[i]=find(fa[i]);
return fa[i];
}
}
int main()
{
scanf("%d %d",&n,&m);
for(int i=1; i<=m; i++)
{
scanf("%d %d %d",&a[i].x,&a[i].y,&a[i].z);
}
init(m); //初始化fa[]
quick(1,m);//升序排序,找最小边
for(int i=1; i<=m; i++) //集合
{
int x=find(a[i].x);
int y=find(a[i].y);
if(x==y) continue;
else
{
fa[x]=y;
ans+=a[i].z;
}
}
for(int i=1; i<=n; i++)
{
if(fa[i]==i)
{
cnt++; //找cnt个集合
}
}
if(cnt>1) printf("orz\n"); //只能有一个集合
else printf("%lld\n",ans);
return 0;
}