AdaBoost算法介绍和代码实现

算法原理

AdaBoost算法的核心思想是将弱分类器组合成一个强分类器。在每一轮迭代中，AdaBoost会训练一个新的弱分类器并调整每个样本的权重，使得之前分类错误的样本在下一轮迭代中受到更多的关注。最终，AdaBoost将所有弱分类器的预测结果加权求和，得到最终的分类结果。

具体来说，AdaBoost算法的步骤如下：

1. 初始化样本权重：给每个样本赋予相等的权重，即$w_i=1/N$，其中$N$是样本数量。

2. 迭代训练基本分类器：在每个迭代中，使用当前样本权重训练一个基本分类器，并计算该分类器的误差率。误差率定义为分类错误的样本数量除以总样本数量。

3. 计算基本分类器的权重：根据分类器的误差率计算其相应的权重，其中误差率越低的分类器获得的权重越高。具体计算公式为$w_j=\frac{1}{2}\ln (\frac{1-{ϵ}_j}{{ϵ}_j})$，其中${ϵ}_j$是第$j$个分类器的误差率。

4. 更新样本权重：对于每个样本，如果它被正确分类，则降低其权重；如果它被错误分类，则提高其权重。具体公式为$w_i^{(t+1)}=\frac{w_i^{(t)}\exp (-{\alpha }_t{y}_i{h}_t(x_i))}{Z_t}$，其中${\alpha }_t$是第$t$轮迭代的分类器权重，$y_i$是样本$i$的真实标签，$h_t(x_i)$是第$t$轮迭代的分类器对样本$i$的预测结果，$Z_t$是规范化因子，使得新的样本权重之和为1。

5. 组合基本分类器：将所有基本分类器组合成一个强分类器，其中每个分类器的权重等于其相应的权重。

代码实现

以下是一个使用Python和scikit-learn库实现的AdaBoost算法示例：

# 导入所需的库和数据集
from sklearn.ensemble import AdaBoostClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# 加载数据集
data = load_iris()
X, y = data.data, data.target

# 将数据集分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# 初始化AdaBoost算法，并使用两种不同的基本分类器
base_estimators = [
    DecisionTreeClassifier(max_depth=1),  # 使用深度为1的决策树作为第一个基本分类器
    SVC(kernel='linear', C=1.0)          # 使用线性SVM作为第二个基本分类器
]
n_estimators = 50                        # 设置迭代次数为50
learning_rate = 1.0                      # 设置学习率为1.0
#使用AdaBoost算法创建分类器对象clf，estimator参数指定使用的基本分类器，这里选择使用base_estimators列表中的第一个元素，即深
#度为1的决策树
clf = AdaBoostClassifier(estimator=base_estimators[0], n_estimators=n_estimators, learning_rate=learning_rate)

# 在训练集上拟合模型
clf.fit(X_train, y_train)

# 在测试集上评估模型
y_pred = clf.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy: %.2f%%" % (accuracy * 100.0))

在以上示例中，我们首先使用load_iris函数加载鸢尾花数据集，然后将数据集分为训练集和测试集。接着，我们初始化一个AdaBoost分类器，其中基本分类器是深度为1的决策树，迭代次数为50，学习率为1.0。最后，我们在训练集上拟合模型，并在测试集上评估模型的准确性。

在AdaBoost算法中，每个基本分类器都被赋予一个权重，这个权重表示了这个基本分类器的重要性。在训练过程中，AdaBoost算法会逐步构建一个强分类器，这个强分类器是基于所有基本分类器的加权组合而成的。

在AdaBoost算法的每一轮迭代中，它会使用当前的强分类器对数据进行分类，并根据分类结果对数据进行加权，以便下一轮迭代可以更好地处理错误分类的数据。具体来说，对于每个被错误分类的样本，AdaBoost算法会增加它的权重，以便下一轮迭代可以更加关注这些错误分类的样本。而对于正确分类的样本，它们的权重会减少，以便下一轮迭代可以更加关注那些难以分类的样本。

在训练过程中，每个基本分类器的权重都是根据它在当前强分类器中的分类性能来确定的。具体来说，分类性能越好的基本分类器，其权重就越大，反之亦然。在每一轮迭代结束后，AdaBoost算法会计算当前强分类器的错误率，并根据错误率来为下一轮迭代中的基本分类器分配权重。

最终，当达到指定的迭代次数或错误率满足要求时，AdaBoost算法会返回一个强分类器，这个强分类器是所有基本分类器的加权组合。这个强分类器可以用于对新样本进行分类，从而实现对未知数据的预测。

调整超参数

可以使用以下代码调整超参数并绘制学习曲线：

import matplotlib.pyplot as plt

# 调整迭代次数
n_estimators_range = range(1, 101, 10)
train_scores = []
test_scores = []
for n_estimators in n_estimators_range:
    clf = AdaBoostClassifier(estimator=base_estimators[0], n_estimators=n_estimators, learning_rate=learning_rate)
    clf.fit(X_train, y_train)
    train_scores.append(clf.score(X_train, y_train))
    test_scores.append(clf.score(X_test, y_test))
plt.plot(n_estimators_range, train_scores, label="Train")
plt.plot(n_estimators_range, test_scores, label="Test")
plt.xlabel("n_estimators")
plt.ylabel("Accuracy")
plt.legend()
plt.show()

# 调整学习率
learning_rate_range = [0.1, 0.5, 1, 2, 5]
train_scores = []
test_scores = []
for learning_rate in learning_rate_range:
    clf = AdaBoostClassifier(estimator=base_estimators[0], n_estimators=n_estimators, learning_rate=learning_rate)
    clf.fit(X_train, y_train)
    train_scores.append(clf.score(X_train, y_train))
    test_scores.append(clf.score(X_test, y_test))
plt.plot(learning_rate_range, train_scores, label="Train")
plt.plot(learning_rate_range, test_scores, label="Test")
plt.xlabel("learning_rate")
plt.ylabel("Accuracy")
plt.legend()
plt.show()

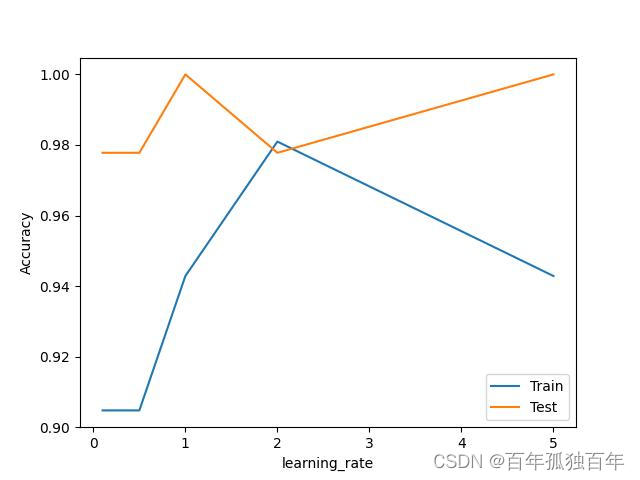
在这里，我们分别调整了迭代次数和学习率两个超参数，并绘制了对应的学习曲线。从学习曲线可以看出，随着迭代次数的增加，模型的准确性逐渐提高，但在达到一定程度后就趋于稳定。同时，随着学习率的增加，模型的准确性会先上升后下降，因此需要进行适当的调参。需要注意的是，实际应用中还可以调整其他超参数，例如基本分类器的深度、支持向量机的核函数等，以获得更好的性能。

总结

总之，AdaBoost算法是一种强大的集成学习方法，可以将多个弱分类器组合成一个强分类器，从而提高模型的准确性和泛化能力。在实际应用中，我们可以根据具体问题选择不同的基本分类器和调整不同的超参数，以获得最佳的性能。

需要注意的是，AdaBoost算法对基本分类器的要求比较宽松，可以使用任何分类器作为基本分类器，例如决策树、支持向量机等。同时，调整迭代次数和学习率等超参数也会对模型性能产生影响，需要进行适当的调参。