嵌入式软件开发，非科班专业必须掌握的基本计算机知识

核心知识点：数据表示和运算、存储系统、指令系统、总线系统、中央处理器、输入输出系统

一 进位计数法和不同进制数的相互转换

其他进制(b)，转十进制的计算公式 

十进制数，转其他进制(b)，实际上就是求Ai的过程

对于整数部分，第i次除以基数b所得到的余数即为Ai,(i为1、2、..、n)
对于小数部分，第i次乘以基数b所得到的整数部分即为A-i.(i为0、1、...、n）
注意每次乘法之后要把个位置0

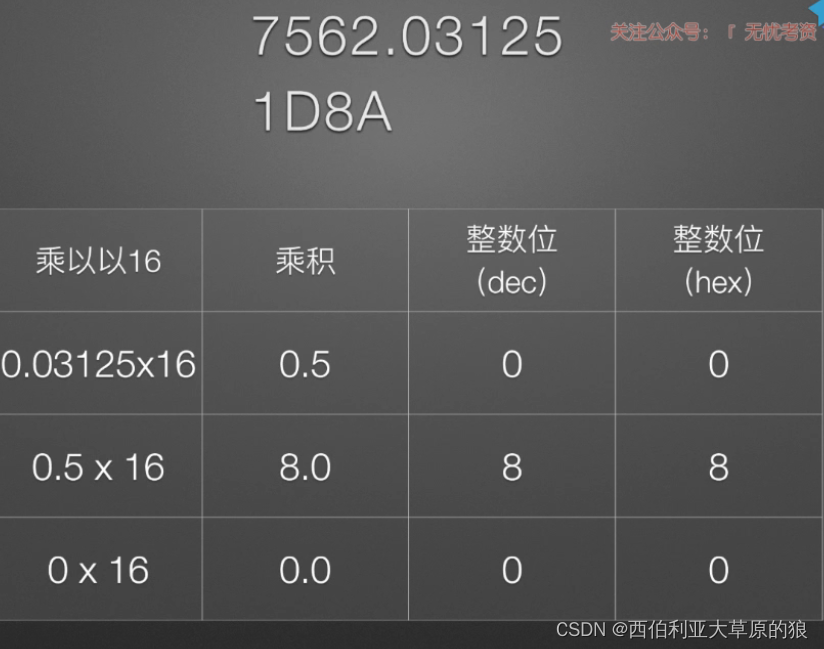
例：十进制7562.03125转十六进制 . 结果为1D8A.08

二进制和八进制、十六进制互相转换

八进制就三个一位，十六进制就四个一位

 二 BCD码和校验码

1、BCD码 一种编码方式，用二进制来编码的十进制数，常用的为8421码、2421码、余3码

2、传输数据校验：奇偶校验码

奇校验码：整个校验码中1的个数为奇数

偶校验码：整个校验码中1的个数为偶数 

3、海明码 （不仅能发现错误，还能纠正错误）

设：数据有m（message）位，校验码有p（parity）位：

则：校验码一共有2的p次方种取值；

若想通过校验码指出任一位上发生的错误必须满足：

2p-1>=m+p

由m = 4，得p >= 3

要求，在2的n次方的位置上，其次，校验码要与数据位建立某种关系，方便纠错

p1、p2、p3处是0还是1，是根据要求的奇偶校验来的。

4 循环冗余校验码（多项式校验码）（CRC校验码）

循环冗余校验码（Cyclic Redundancy Check，CRC）是一种常用的网络传输错误检测技术。该技术通过将要传输的数据进行编码，并在接收端对接收到的数据进行解码，从而验证数据传输中是否发生了错误。 CRC 算法的基本思想是在原数据后面添加若干个位数为 0 的校验码，然后根据这些数据计算出一个固定长度的校验码，将其添加到数据中一起传输。接收端再次计算校验码，与接收到的校验码进行比较，如果不一致则说明数据传输存在错误。

CRC 算法的特点是具有“循环性”，即生成校验码的过程可以看做将原数据序列除以一个固定的除数，在模 2 加法下得到的余数。因此，CRC 码也被称为循环码。同时，CRC 码的长度通常为 16 位、32 位、64 位等固定长度，不同的长度会影响校验码的重复周期，从而影响误检率和漏检率。

CRC 码的优点是具有高效性和可靠性，可以在不增加数据传输量和延迟的情况下完成检测任务，并且在大多数情况下可以实现无误检。同时，CRC 码的应用范围非常广泛，包括数据通信、存储介质、无线电通信等多个领域。

三 定点数的表示和运算

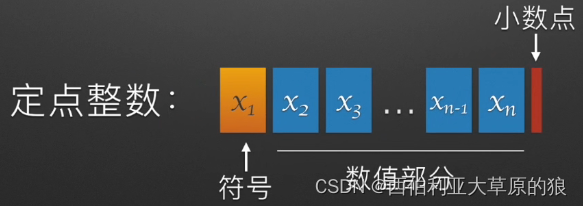
在计算机中，定点数是指采用固定小数点位数的一种表示方法，该表示方法将小数点固定在某一位置（因为计算机中不会去存储一个小数点），通常是小数点右边第 n 位，然后将整数和小数部分分别存储在不同的位域中，以便计算机能够对它们进行运算处理。定点数通常用于表示需要高精度计算的数据，如金融数据和图像处理等领域。

在定点数表示法中，整数部分和小数部分所占的位数是一定的，这意味着它们所能表示的范围和精度是固定的。例如，如果采用 16 位的定点数表示法，其中 8 位表示整数，8 位表示小数，则可以表示的最大值是 2^7-1.999（即最高位为符号位），而且只能表示到 2^-8 的精度。因此，在使用定点数进行计算时，需要事先考虑好精度和范围的限制，以免出现截断误差等问题。

另外，相对于浮点数来说，定点数的计算速度更快、精度更高，但是它的表示范围和可调节精度较少。因此，在具体应用中需根据实际情况选择合适的表示方法。

 

 

知识点：真值（实际值，有正负号）与机器数（没有正负号，用01代替）

机器数的有符号数、有原码、补码、反码、移码四种形式

机器数的原码表示

但现在仍存在一个问题，即机器数做加法只能两个正数相加、而不能加负数，因此可以借助时钟原理 改为 +1 0 0 0 0

机器数的补码表示（负值不同）

机器数的反码表示

定点数的移位运算

 

定点数的加减运算，注意：符号位也参与运算（需要注意溢出判断）

原码与补码互相转换公式

溢出判断，两个正数相加得负数，原因是数值位不足。 

（正数加正数、负数加负数、正数减负数、负数减正数）

基于一位符号位做溢出判断

基于两位符号位做溢出判断

 

定点数的乘法运算 

定点数的除法运算

四 浮点数的表示和运算

计算机中的表示方式

其中阶码反映浮点数的范围大小和小数点的实际位置

其中尾数反映浮点数的精度

规格化浮点数（把尾数（非零）最高位为有效值的浮点数称之为规格化浮点数）

浮点数的加减法

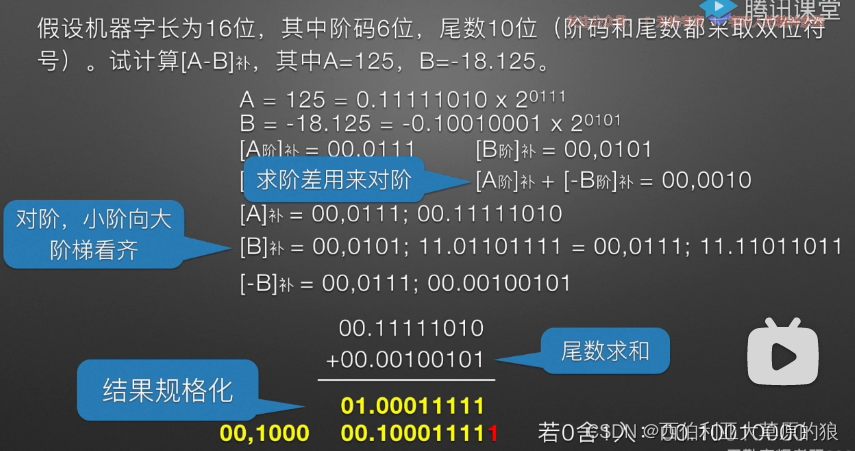
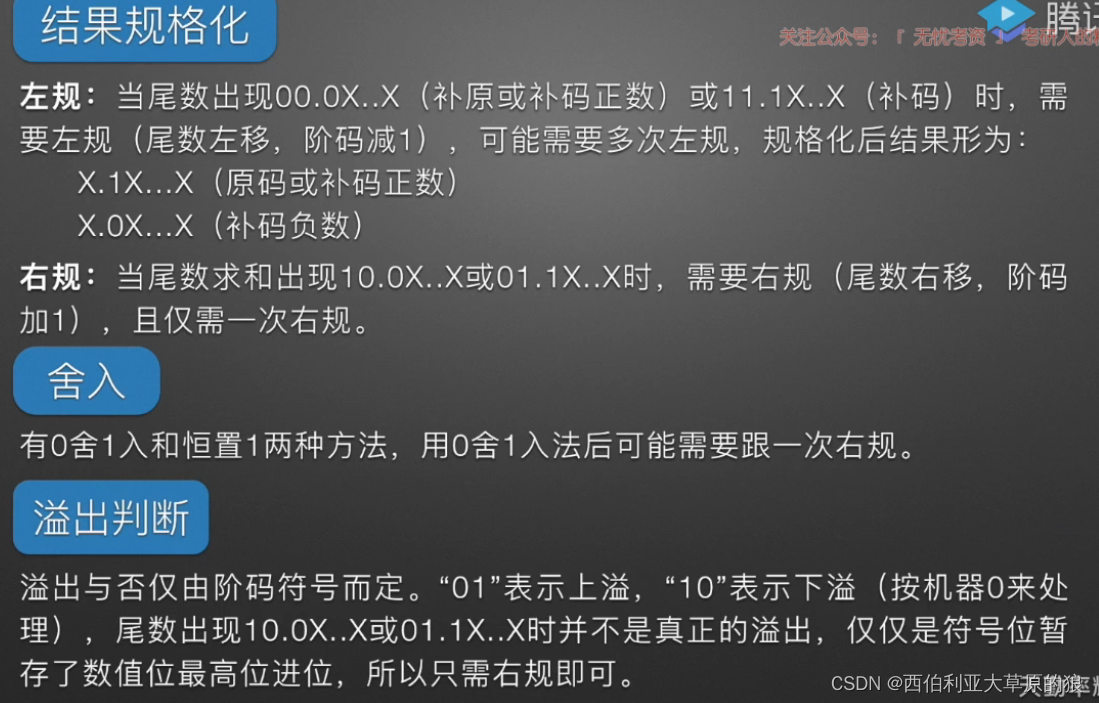
结果规格化的左规与右规、舍入、溢出判断

五 IEEE754标准及ALU

算术逻辑单元ALU

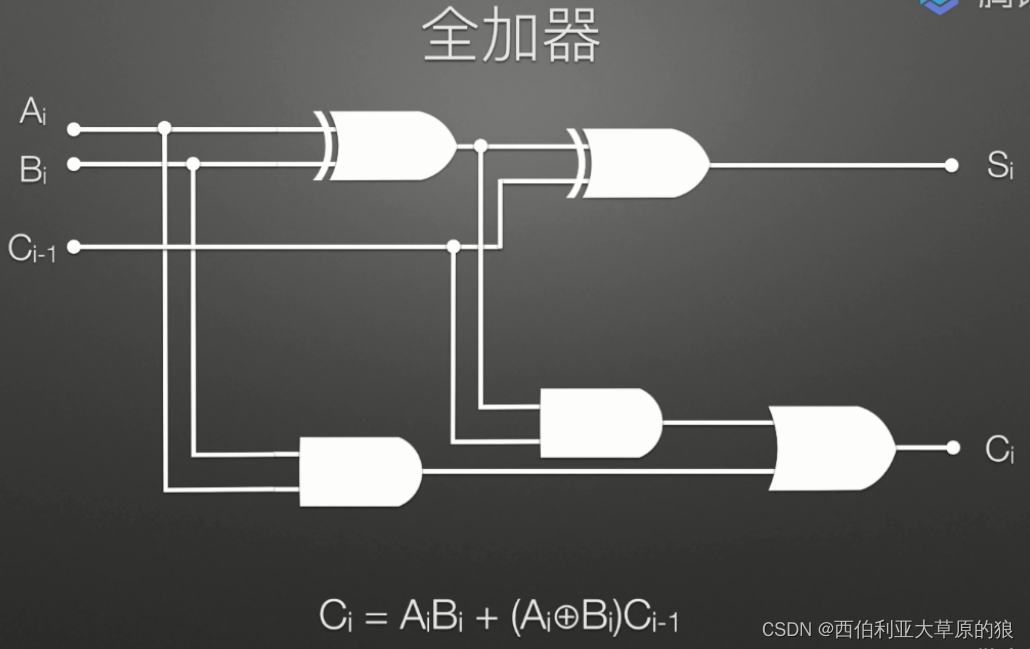
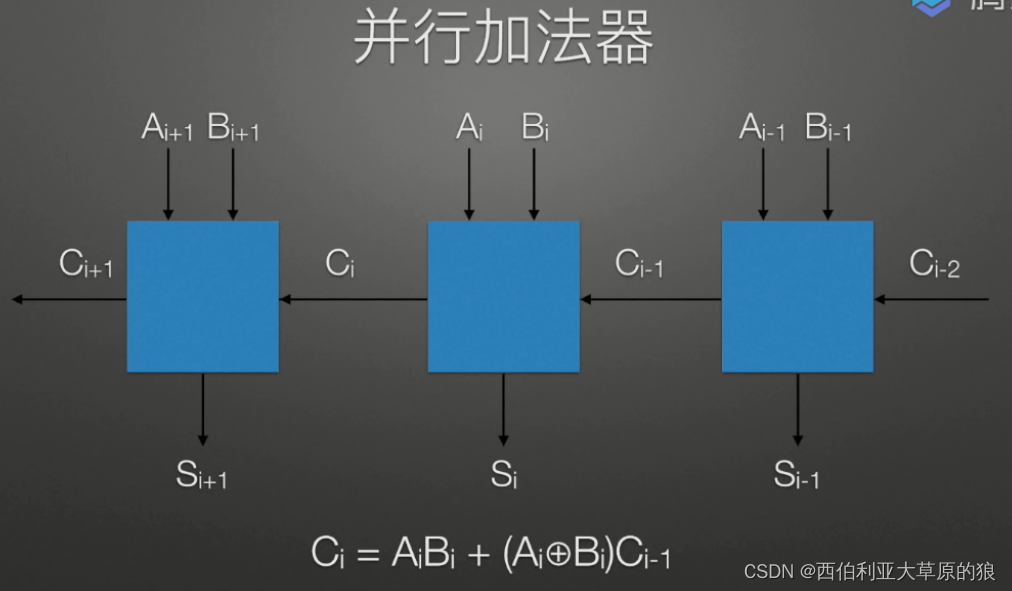
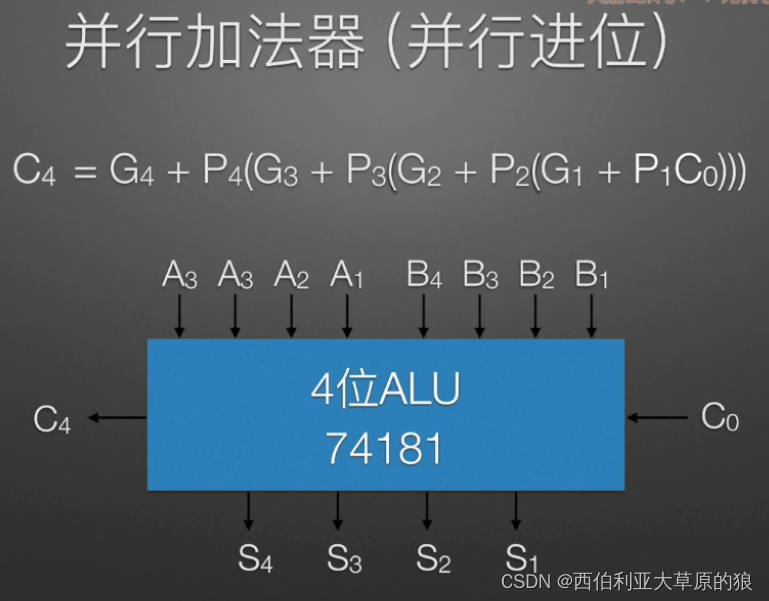
算术逻辑单元（Arithmetic Logic Unit，简称 ALU）是计算机的重要组成部分之一，用于执行各种算术和逻辑运算。它位于CPU核心中央，主要负责对寄存器中的数据进行加减乘除、与或非、移位等运算操作。

ALU 由多个基本逻辑电路组成，包括加法器、减法器、与门、或门、非门等。其中加法器和减法器是 ALU 的核心部件，它们用于执行加减运算。与门、或门和非门则主要用于逻辑运算，比如与、或、非等。移位电路则用于在二进制数中实现左移和右移操作。

ALU 的输入是来自寄存器中的两个数据和一个控制信号，控制信号指示需要执行何种运算操作。输出则是运算结果，也保存在寄存器中以供后续的运算使用。

ALU 的性能对整个计算机的运行速度和效率有很大影响。因此，在设计 ALU 时，需要考虑到寄存器数量、位数、运算类型和速度等因素，以满足不同应用场景的需求。同时，了解和掌握 ALU 的工作原理和结构，对于深入理解计算机的运行原理和进行计算机系统设计和开发等方面都具有重要意义。