DDPM–生成扩散模型
Github: https://github.com/daiyizheng/Deep-Learning-Ai/blob/master/AIGC/Diffusion.ipynb
DDPM 是当前扩散模型的起点。在本文中,作者建议使用马尔可夫链模型,逐步向图像添加噪声。

函数
q
(
x
t
∣
x
t
−
1
)
q(x_t | x_t-1)
q(xt∣xt−1)用于一次一步地向图像添加噪声。在每一步,更多的噪声被添加到图像中,直到图像在 time 时基本上是纯高斯噪声T。
正向过程
从时间t=0到时间t= t,通过向输入图像中逐渐添加更多的噪声称为前向过程(即使它在图像中是向后的)。函数q定义了前向过程,并有一个封闭的解,允许我们直接对给定x的前向过程建模(图像,x,在扩散时间步长0,原始图像)。函数定义如下:
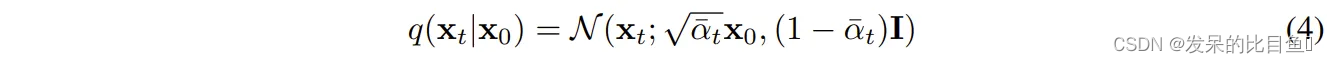
函数q使用正态(高斯)分布来模拟噪声过程。然而,这种方法有一个问题。该分布必须采样t次才能从t=0得到时刻t的图像。我们可以将所有t值的所有图像存储在内存中,或者根据需要从磁盘加载它们,但是t的正常值大于或等于1000,因此我们必须存储每个图像的1000个变体来训练模型,这是不希望的。
为了解决这些问题,作者对前向过程进行了如下建模

这种方法使用了重参数化技巧,它允许我们对分布进行建模,但在某种程度上,我们可以根据
α
ˉ
\bar{\alpha}
αˉ直接从时间步长0跳到t。在某种程度上,上面的公式是根据
α
ˉ
t
\bar{\alpha}_t
αˉt(噪声调度器)对
x
x
x(原始图像)和
ϵ
\epsilon
ϵ(从正态分布中采样的噪声)进行加权。
α
ˉ
t
\bar{\alpha}_t
αˉt条是基于噪声调度器计算的。该值越低,添加的噪声越多。作者将
α
t
α_t
αt定义为
1
−
β
t
1-β_t
1−βt,
α
ˉ
\bar{\alpha}
αˉ定义为从时间0到时间t的
α
t
α_t
αt值的累积。

β
t
β_t
βt是噪声调度器。DDPM论文的作者使用了一个介于
1
0
−
4
10^{-4}
10−4和
0.02
0.02
0.02之间的线性调度器。在时间
t
=
0
t=0
t=0时,
β
t
β_t
βt的值将是
1
0
−
4
10^{-4}
10−4。在
T
T
T时刻,
β
t
β_t
βt为0.02。这些值有点像在时间
t
t
t上的噪声量相对于时间
t
−
1
t-1
t−1的百分比。
请注意,在时间t处添加的噪声量不仅仅是在 1 0 − 4 10^{-4} 10−4和 0.02 0.02 0.02之间的比率,而是我们使用 α ˉ t \bar{\alpha}_t αˉt。此外, α ˉ t \bar{\alpha}_t αˉt是从0到t的所有 α t α_t αt值的乘积。因此,在时间t处添加的噪声是所有 α t α_t αt值的乘积,这意味着每个时间步长的噪声量呈指数级增长,原始图像的百分比呈指数级下降。下面的曲线显示了从 t = 0 t=0 t=0到 t = 1000 t=1000 t=1000的所有时间步长的 α t α_t αt值。

为了总结前向过程,我们可以使用q函数的封闭形式解在单个操作中从
x
0
x_0
x0(原始图像)到
x
t
x_t
xt(扩散步骤t的图像)向图像添加噪声。
向后过程
反向过程模拟
q
(
x
∣
x
t
−
1
)
q(x | x_{t-1})
q(x∣xt−1)的反向过程,由函数
p
(
x
t
−
1
∣
x
)
p(x_{t-1} |x)
p(xt−1∣x)给出。不幸的是,我们不能直接对这个过程建模,因为当我们想要得到图像
x
x
x时,图像
x
t
−
1
x_{t-1}
xt−1有太多的可能性。
我们可以使用神经网络来估计反向过程。因此,函数变成了
p
θ
(
x
∣
x
t
−
1
,
t
)
p_θ(x | x_{t-1}, t)
pθ(x∣xt−1,t)。
θ
θ
θ表示我们正在优化的神经网络的参数,以估计函数
p
p
p。
直观地说,由于我们使用正态分布来模拟正向过程,我们也可以使用正态分布来模拟反向过程。因此,我们可以让模型预测正态分布的平均值和方差,其中
µ
θ
µ_θ
µθ是分布的预测,而
σ
θ
σ_θ
σθ是预测方差或分布。注意,这个正态分布是对所有像素进行预测的;它不是整个图像的一个正态分布。
p
θ
(
x
t
−
1
∣
x
t
)
:
=
N
(
x
t
−
1
;
μ
θ
(
x
t
,
t
)
,
Σ
θ
(
x
t
,
t
)
)
p_\theta\left(x_{t-1} \mid x_t\right):=\mathcal{N}\left(x_{t-1} ; \mu_\theta\left(x_t, t\right), \Sigma_\theta\left(x_t, t\right)\right)
pθ(xt−1∣xt):=N(xt−1;μθ(xt,t),Σθ(xt,t))
我们还看到,与固定方差相比,学习反向过程方差(通过将参数化对角线
Σ
θ
(
x
t
)
Σ_θ(x_t)
Σθ(xt)纳入变分界)导致训练不稳定和样本质量较差。(4.2) DDPM作者发现保持方差
Σ
θ
Σ_θ
Σθ恒定(我们将在下一节中详细讨论)要容易得多,并且他们设置
Σ
θ
=
β
t
Σ_θ=β_t
Σθ=βt,因为
β
t
β_t
βt是时间步长t的噪声方差。
由于我们知道使用函数 q ( x t ∣ x t − 1 ) q(x_t | x_{t -1}) q(xt∣xt−1)使我们步进t的正态分布,并且我们对该分布有一个预测 p ( x t − 1 ∣ x t ) p(x _{t-1} |x_t) p(xt−1∣xt),我们可以使用两个分布之间的KL散度损失来优化模型。
作者指出,由于他们保持方差不变,他们只需要预测分布的均值。更好的是,我们可以预测从正态分布中采样并通过重新参数化技巧添加到图像中的噪声ε。作者发现,预测噪音更加稳定。由于我们只需要预测添加的噪声,我们可以使用预测噪声和添加到图像中的实际噪声之间的MSE损失。
Model:
ϵ
θ
(
α
ˉ
t
x
0
+
1
−
α
ˉ
t
ϵ
)
\epsilon_\theta\left(\sqrt{\bar{\alpha}_t} x_0+\sqrt{1-\bar{\alpha}_t} \epsilon\right)
ϵθ(αˉtx0+1−αˉtϵ)
Loss:
M
S
E
[
ϵ
−
ϵ
θ
(
α
ˉ
t
x
0
+
1
−
α
ˉ
t
ϵ
)
]
\quad M S E\left[\epsilon-\epsilon_\theta\left(\sqrt{\bar{\alpha}_t} x_0+\sqrt{1-\bar{\alpha}_t} \epsilon\right)\right]
MSE[ϵ−ϵθ(αˉtx0+1−αˉtϵ)]
有人可能会认为模型很难学习噪声,因为噪声是随机的,而神经网络通常是确定的。但是,如果我们给模型在时间t和时间步长t的噪声图像,那么模型可以找到一种方法从噪声图像中提取噪声,这可以用来反转噪声过程。
有趣的是,作者特别指出,我们在第4节中的扩散过程设置使简化的目标降低了与小t对应的损失项的权重。这些项训练网络以非常少量的噪声去噪数据,因此降低它们的权重是有益的,这样网络就可以专注于更大t项下的更困难的去噪任务。(第5页,第3.4部分)
因此,作者构建了损失,使模型更倾向于学习较高的t值,这需要它去噪比较低的t值更多的噪声。其思想是,较高的t值构建对象的高级特征,较低的t值构建图像中更细粒度的特征。使物体的主要形状正确比使物体具有某种纹理更重要。
反向过程通常使用U-net建模,如下所示

输入是时刻t的图像,输出是图像中的噪声。此外,在网络的每一层,我们添加了时间信息,以帮助模型知道它在扩散过程中的位置。
循环训练
通过定义向前和向后的过程,我们可以训练模型并通过以下training/denoising循环生成图像:

代码
import torch.nn as nn
import torch
from torch.utils.data import DataLoader
from tqdm import tqdm
import matplotlib.pyplot as plt
import numpy as np
import math
from torchvision import datasets, transforms
torch.manual_seed(0)
class SinusoidalPositionEmbeddings(nn.Module):
def __init__(self, total_time_steps=1000, time_emb_dims=128, time_emb_dims_exp=512) -> None:
super().__init__()
half_dim = time_emb_dims//2
emb = math.log(10000) / (half_dim - 1)
emb = torch.exp(torch.arange(half_dim, dtype=torch.float32) * -emb)
ts = torch.arange(total_time_steps, dtype=torch.float32)
emb = torch.unsqueeze(ts, dim=-1) * torch.unsqueeze(emb, dim=0)
emb = torch.cat((emb.sin(), emb.cos()), dim=-1)
self.time_block = nn.Sequential(
nn.Embedding.from_pretrained(emb),
nn.Linear(in_features=time_emb_dims, out_features=time_emb_dims_exp),
nn.SiLU(),
nn.Linear(in_features=time_emb_dims_exp, out_features=time_emb_dims_exp)
)
def forward(self, time):
return self.time_block(time)
class DownSample(nn.Module):
def __init__(self, channels) -> None:
super().__init__()
self.downsample = nn.Conv2d(in_channels=channels,
out_channels=channels,
kernel_size=3,
stride=2,
padding=1)
def forward(self, x, *args):
return self.downsample(x)
class UpSample(nn.Module):
def __init__(self, in_channels) -> None:
super().__init__()
self.upsample = nn.Sequential(
nn.Upsample(scale_factor=2, mode="nearest"),
nn.Conv2d(in_channels=in_channels,
out_channels=in_channels,
kernel_size=3,
stride=1,
padding=1))
def forward(self, x, *args):
return self.upsample(x)
class AttentionBlock(nn.Module):
def __init__(self, channels=64) -> None:
super().__init__()
self.channels = channels
self.group_norm = nn.GroupNorm(num_groups=8, num_channels=channels)
self.mhsa = nn.MultiheadAttention(embed_dim=self.channels, num_heads=4, batch_first=True)
def forward(self, x):
B, _, H, W = x.shape
h = self.group_norm(x)
h = h.reshape(B, self.channels, H*W).swapaxes(1, 2) # [B, C, H, W] --> [B, C, H * W] --> [B, H*W, C]
h, _ = self.mhsa(h, h, h)
h = h.swapaxes(2, 1).view(B, self.channels, H, W) # [B, C, H*W] --> [B, C, H, W]
return x+h
class ResnetBlock(nn.Module):
def __init__(self,
in_channels,
out_channels,
dropout_rate=0.1,
time_emb_dims=512,
apply_attention=False) -> None:
super().__init__()
self.in_channels = in_channels
self.out_channels = out_channels
self.act_fn = nn.SiLU()
# Group 1
self.normlize_1 = nn.GroupNorm(num_groups=8,
num_channels=self.in_channels)
self.conv_1 = nn.Conv2d(in_channels=self.in_channels,
out_channels=self.out_channels,
kernel_size=3,
stride=1,
padding="same")
# Group 2 time embedding
self.dense_1 = nn.Linear(in_features=time_emb_dims, out_features=self.out_channels)
# Group 3
self.normlize_2 = nn.GroupNorm(num_groups=8, num_channels=self.out_channels)
self.dropout = nn.Dropout2d(p=dropout_rate)
self.conv_2 = nn.Conv2d(in_channels=self.out_channels,
out_channels=self.out_channels,
kernel_size=3,
stride=1,
padding="same")
if self.in_channels != self.out_channels:
self.match_input = nn.Conv2d(in_channels=self.in_channels,
out_channels=self.out_channels,
kernel_size=1, stride=1)
else:
self.match_input = nn.Identity()
if apply_attention:
self.attention = AttentionBlock(channels=self.out_channels)
else:
self.attention = nn.Identity()
def forward(self, x, t):
# group 1
h = self.act_fn(self.normlize_1(x))
h = self.conv_1(h)
# group 2
# add in timestep embedding
h += self.dense_1(self.act_fn(t))[:, :, None, None] #
# group 3
h = self.act_fn(self.normlize_2(h))
h = self.dropout(h)
h = self.conv_2(h)
# Residual and attention
h = h + self.match_input(x)
h = self.attention(h)
return h
class Unet(nn.Module):
def __init__(self,
input_channels=3,
output_channels=3,
num_res_blocks=2,
base_channels=128,
base_channels_multiples=(1, 2, 4, 8),
apply_attention=(False, False, True, False),
dropout_rate=0.1,
time_multiple=4,
) -> None:
super().__init__()
time_emb_dims_exp = base_channels * time_multiple # 32 * 4=128
self.time_embeddings = SinusoidalPositionEmbeddings(time_emb_dims=base_channels,
time_emb_dims_exp=time_emb_dims_exp)
self.first = nn.Conv2d(in_channels=input_channels,
out_channels=base_channels,
kernel_size=3, stride=1, padding="same")
num_resolutions = len(base_channels_multiples)
# Encoder part of The Unet. Dimension reduction
self.encoder_blocks = nn.ModuleList()
curr_channels = [base_channels]
in_channels = base_channels
for level in range(num_resolutions):
out_channels = base_channels * base_channels_multiples[level]
for _ in range(num_res_blocks):
block = ResnetBlock(
in_channels=in_channels,
out_channels=out_channels,
dropout_rate=dropout_rate,
time_emb_dims=time_emb_dims_exp,
apply_attention=apply_attention[level],
)
self.encoder_blocks.append(block)
in_channels = out_channels
curr_channels.append(in_channels)
if level != (num_resolutions - 1):
self.encoder_blocks.append(DownSample(channels=in_channels))
curr_channels.append(in_channels)
# Bottleneck in between
self.bottleneck_block = nn.ModuleList(
(
ResnetBlock(
in_channels=in_channels,
out_channels=in_channels,
dropout_rate=dropout_rate,
time_emb_dims=time_emb_dims_exp,
apply_attention=True
),
ResnetBlock(
in_channels=in_channels,
out_channels=in_channels,
dropout_rate=dropout_rate,
time_emb_dims=time_emb_dims_exp,
apply_attention=False,
)
)
)
# Decoder part of the Unet. Dimension restoration with skip-connections.
self.decoder_blocks = nn.ModuleList()
for level in reversed(range(num_resolutions)):
out_channels = base_channels * base_channels_multiples[level]
for _ in range(num_res_blocks+1):
encoder_in_channels = curr_channels.pop()
block = ResnetBlock(
in_channels=encoder_in_channels+in_channels,
out_channels=out_channels,
dropout_rate=dropout_rate,
time_emb_dims=time_emb_dims_exp,
apply_attention=apply_attention[level]
)
in_channels = out_channels
self.decoder_blocks.append(block)
if level !=0:
self.decoder_blocks.append(UpSample(in_channels=in_channels))
self.final = nn.Sequential(
nn.GroupNorm(num_groups=8, num_channels=in_channels),
nn.SiLU(),
nn.Conv2d(in_channels=in_channels, out_channels=output_channels, kernel_size=3, stride=1, padding="same")
)
def forward(self, x, t):
time_emb = self.time_embeddings(t)
h = self.first(x)
outs = [h]
for layer in self.encoder_blocks:
h = layer(h, time_emb)
outs.append(h)
for layer in self.bottleneck_block:
h = layer(h, time_emb)
for layer in self.decoder_blocks:
if isinstance(layer, ResnetBlock):
out = outs.pop()
h = torch.cat([h, out], dim=1)
h = layer(h, time_emb)
h = self.final(h)
return h
model = Unet(input_channels=1,
output_channels=1,
base_channels=64,
base_channels_multiples=(1, 2, 4, 8),
apply_attention=(False, False, True, False),
dropout_rate=0.1,
time_multiple=2)
batch_timesteps = torch.arange(128)
X_train = torch.randn((128, 1, 32, 32))
model(X_train, batch_timesteps)
参考
https://betterprogramming.pub/diffusion-models-ddpms-ddims-and-classifier-free-guidance-e07b297b2869






![[oeasy]python0048_注释_comment_设置默认编码格式](https://img-blog.csdnimg.cn/img_convert/0dbeb554a0180969f21851440d52e6ff.png)
