动态规划 — 01背包
一直到现在都非常害怕动态规划,因为基本上自己都无法想出dp递推式,太难受了 T.T
今天再一次遇到了需要写01背包的情况,根据自己学习的一点点经历,再稍微总结一下01背包吧,虽然是个被认为dp入门的经典题,但还是希望自己对dp的理解可以更进一步吧。
题目描述
0-1背包的问题提出是,有n个物品,其中物品i的重量是wi,价值为vi,有一容量为C的背包,要求选择若干物品装入背包,使得装入背包的物品总价值达到最大。每个物品只能选择一次。
更加数学化描述:给定 C > 0,wi > 0,vi > 0,1 <= i <= n ,要求找出n元0-1向量(x1,x2,…,xn) xi ∈{0,1},1 <= i <= n ,使得目标函数 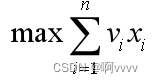
达到最大,并且要满足约束条件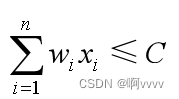
解题
对于每一个物品,我们只有放入背包,或者不放入背包两种可能性,所以我们直接枚举,对,你没看错,直接枚举。

方法一:暴力递归枚举
写递归,需要明确两点,继续递归的条件(变量的变化方向)解递归的条件(变量至何情况不会变)
对于本题,物品是有限的,背包容量是有限的,所以肯定会有两个变量。
//暴力递归
int process1(int index,int bagWeight,int[] weights,int [] values){
//没东西拿
if(index >= weights.length){
return 0;
}
//装不下
if(bagWeight < 0){
return 0;
}
//对于当前物品,只有选择与不选择
//选择
int tmp1 = 0;
//必须选择可以放的下的物品
if(bagWeight - weights[index] >= 0){
tmp1 = values[index] + process(index + 1, bagWeight - weights[index], weights, values);
}
//不选择
int tmp2 = process(index + 1, bagWeight, weights, values);
return Math.max(tmp1, tmp2);
}
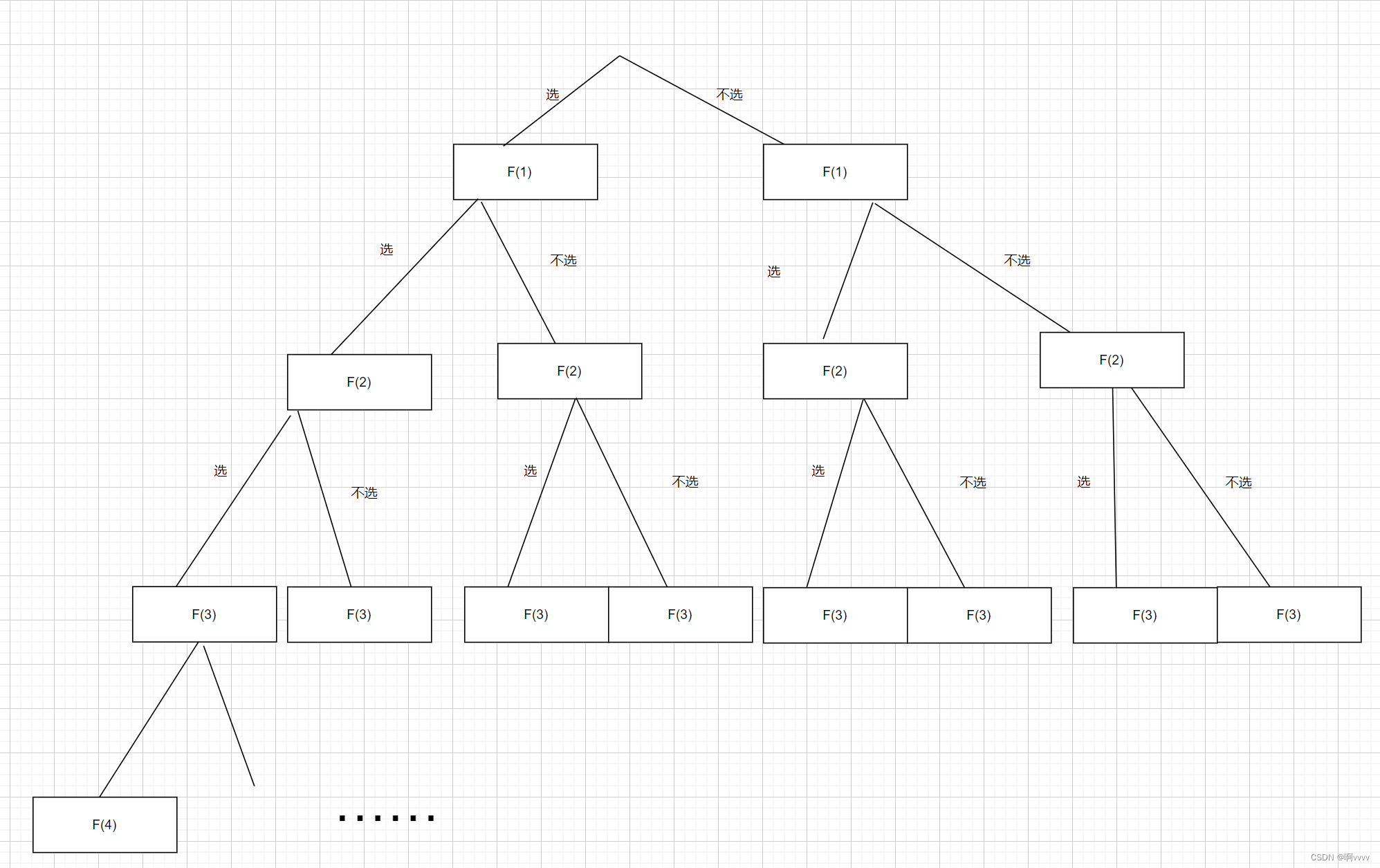
优化
从上图我们看到了有很多重复的解,既然如此,何必不存起来呢?所以我们增加一个缓存,计算过的结果我们不再计算
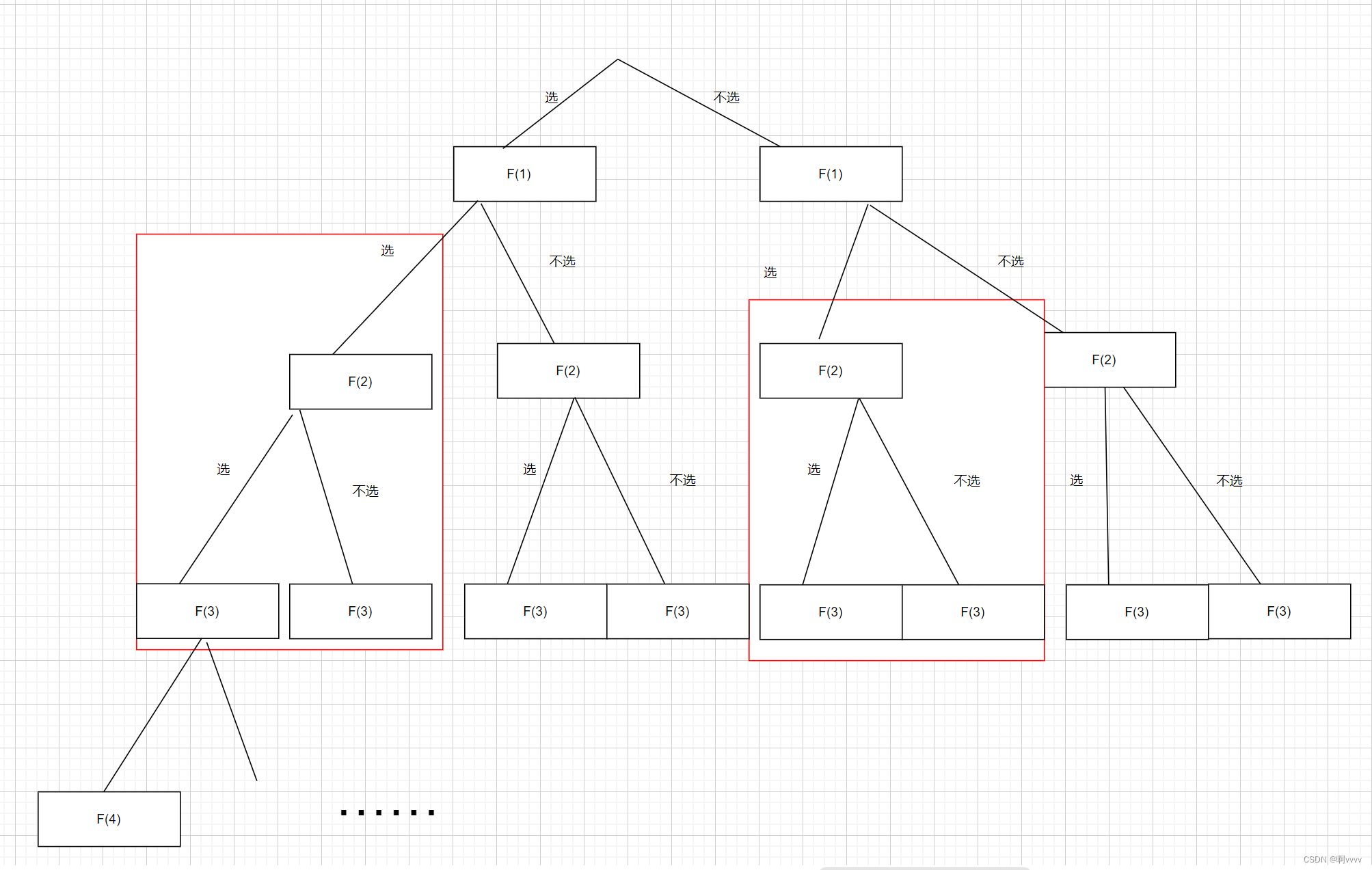
//记忆化递归
int process2(int index,int bagWeight,int[] weights,int [] values, HashMap<Integer,Integer> cache{
//没东西拿
if(index >= weights.length){
return 0;
}
//装不下
if(bagWeight < 0){
return 0;
}
//先走缓存
//对于当前物品,只有选择与不选择
//选择
if(cache.get(index) == null){
int tmp1 = 0;
if(bagWeight - weights[index] >= 0){
tmp1 = values[index] + process(index + 1, bagWeight - weights[index], weights, values);
}
//不选择
int tmp2 = process(index + 1, bagWeight, weights, values);
int max = Math.max(tmp1, tmp2);
//将结果放入缓存
cache.put(index,max);
return max;
}else {
return cache.get(index);
}
}
方法二:动态规划
暴力递归也就俩变量,我全部给他装起来,也就成了二维DP。
其实到动态规划也非常明了了,最优子结构也就是继续递归的条件,而dp数组,就是对某个背包容量的求解结果得存储。我们来写动态规划。以此为例:weights = {5,4,8,6,9} values = {20,6,8,15,18} bagWeight = 18
物品 0 - i,0 <= i < weights.length
背包容量 0 - j, 0 <= j <= bagWeight
请一定记住 i 与 j 所代表得意义!!!
先画一张表格。
初始化表格。咱们从左往右填
当背包容量 j 为0时,无法装下任何物品,所以最大价值都是0。当只有一个物品的时候,只有 j >= weights[0] 才可以将第一个物品装入背包而且其最大价值就是values[0]

第二行
(这里的背包指 dp[i] [1] 容量为1的背包,dp[i] [2] 容量为2的背包……dp[i] [j] 容量为j的背包)
加入第二个物品,如何寻找最大的价值?当然是找到装入第一个背包时的最大价值啦,所以遍历所有背包。
重量不够怎么能加入进来?所以在 j < weights[i] 时,直接抄上一行的,即继承上一个背包的最大价值数组。
重量够了,那么就需要作出判断:当前物品我到底是要还是不要?我要,则当前 最优价值是 上一个物品在背包容量为 j - weights[i] 时的最大价值再加上当前物品的价值 dp[i-1] [ j - weights[ i ] ] + values[i],我不要,则继承上一个物品在背包容量为 j 时的最大价值的最大价值 dp[i-1] [j]。
因此,我们发现了dp 递推式 dp[i ] [ j ] = Math.max(dp[i - 1] [ j ],dp[i - 1] [ j - weights [ i ] ] + values[i]),也就是所谓的最优子结构

看到没?从何处开始变化的?只要当前背包有余量可以某一个添加物品,就会进行比较择优。
第三行

第四行

第五行

//动态规划
int process3(int bagWeight,int[] weights,int [] values){
int[][] dp = new int[weights.length][bagWeight+1];
//初始化
//当只有0号物品的时候
for(int j = 0; j <= bagWeight; j++){
dp[0][j] = j >= weights[0] ? values[0] : 0;
}
for(int i = 1; i < weights.length; i++){
for(int j = 0; j <= bagWeight; j++){
if(j < weights[i]){
dp[i][j] = dp[i-1][j];
}else {
dp[i][j] = Math.max(dp[i - 1][j],dp[i-1][ j - weights[i]] + values[i]);
}
}
}
//打印dp数组
for(int i = 0; i < weights.length; i++){
System.out.println(Arrays.toString(dp[i]));
}
return dp[weights.length-1][bagWeight];
}
优化
对于当前背包容量,我们都是从上一行的记录递推下来所以我们可以舍弃计算过的格子,所以尝试采用一维数组记录,将空间复杂度降下至O (n)。观察最终dp表,每一层都是继承了上一层的背包价值并且与加入当前物品进行了择优。

注意:此处需要倒序遍历,为什么?观察我们两种遍历顺序的结果
我们把dp表打印出来看看
顺序
0
[0, 0, 0, 0, 0, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20]
1
[0, 0, 0, 0, 6, 20, 20, 20, 20, 26, 26, 26, 26, 32, 32, 32, 32, 38, 38]
2
[0, 0, 0, 0, 6, 20, 20, 20, 20, 26, 26, 26, 26, 32, 32, 32, 32, 38, 38]
3
[0, 0, 0, 0, 6, 20, 20, 20, 20, 26, 26, 35, 35, 35, 35, 41, 41, 50, 50]
4
[0, 0, 0, 0, 6, 20, 20, 20, 20, 26, 26, 35, 35, 35, 38, 41, 41, 50, 50]
逆序
0
[0, 0, 0, 0, 0, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20]
1
[0, 0, 0, 0, 6, 20, 20, 20, 20, 26, 26, 26, 26, 26, 26, 26, 26, 26, 26]
2
[0, 0, 0, 0, 6, 20, 20, 20, 20, 26, 26, 26, 26, 28, 28, 28, 28, 34, 34]
3
[0, 0, 0, 0, 6, 20, 20, 20, 20, 26, 26, 35, 35, 35, 35, 41, 41, 41, 41]
4
[0, 0, 0, 0, 6, 20, 20, 20, 20, 26, 26, 35, 35, 35, 38, 41, 41, 41, 44]
在第二行进行计算的时候,非常明显物品0被计算了很多次,为什么?观察递推式:dp[j] = Math.max(dp[j] , dp[j - weights[i]] + values[i]),进行递推的时候,必须保证当前背包 j之前的值是上一个背包继承下来的值。所以必须逆序,否则会多次计算物品价值。
//优化
int process4(int bagWeight,int[] weights,int [] values){
int[] dp = new int[bagWeight+1];
//初始化
//当只有0号物品的时候
for(int j = 0; j <= bagWeight; j++){
dp[j] = j >= weights[0] ? values[0] : 0;
}
for(int i = 1; i < weights.length; i++){
for(int j = bagWeight; j >= weights[i]; j--){
dp[j] = Math.max(dp[j],dp[j-weights[i]] + values[i]);
}
}
//打印dp数组
System.out.println(Arrays.toString(dp));
return dp[bagWeight];
}
结果验证
public static void main(String[] args) {
int[] weights = {5,4,8,6,9};
int[] values = {20,6,8,15,18};
int bagWeight = 18;
int res1 = process(0,bagWeight,weights,values);
System.out.println(res1);
int res2 = process2(0,bagWeight,weights,values,new HashMap<>());
System.out.println(res2);
int res3 = process3(bagWeight,weights,values);
System.out.println(res3);
int res4 = process4(bagWeight, weights, values);
System.out.println(res4);
}
//结果打印
44
44
[0, 0, 0, 0, 0, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20, 20]
[0, 0, 0, 0, 6, 20, 20, 20, 20, 26, 26, 26, 26, 26, 26, 26, 26, 26, 26]
[0, 0, 0, 0, 6, 20, 20, 20, 20, 26, 26, 26, 26, 28, 28, 28, 28, 34, 34]
[0, 0, 0, 0, 6, 20, 20, 20, 20, 26, 26, 35, 35, 35, 35, 41, 41, 41, 41]
[0, 0, 0, 0, 6, 20, 20, 20, 20, 26, 26, 35, 35, 35, 38, 41, 41, 41, 44]
44
[0, 0, 0, 0, 6, 20, 20, 20, 20, 26, 26, 35, 35, 35, 38, 41, 41, 41, 44]
44
总结
关于01背包,为什么要先遍历物品?先遍历背包行不行?为什么第二层循环要逆序?顺序行不行?可以先遍历背包,再遍历物品,遍历可以顺序也可以逆序,这些都可以拿代码进行验证。只不过,遍顺序问题应该对应于题目的含义,这才可以保证直接套用背包模板。本人的理解也大致如此,如果有我有理解错误的地方,还请指出来,大家互相学习。