参考:https://www.zybuluo.com/codeep/note/163962#3%E5%9C%A8%E5%AD%97%E7%AC%A6%E9%97%B4%E5%8A%A0%E5%85%A5%E7%A9%BA%E6%A0%BC
常识、常用
一行公式使用$$开始和结尾,常用符号表示
| 符号 | 功能 |
|---|---|
| $$ | 多行公式的开始和结尾,一个$表示单行公式开始和结尾 |
| \text {注释的文字} | 为了注释文字 |
| _ | 下划线,后边是前面的下标 |
| ^ | 后边是前边的上标 |
| { } | 优先级较高,可以看作是把里边包含的内容做为一部分计算 |
| \或\quad或\qquad或\text{}或\mid | 空格或分割符号,由于转义字符text中的空格是”+空格“ |
| \tag{公式1} | 为了标记公式 |
| \sqrt[根指数]{被开方数} | 根指数省略时是2,例如\sqrt[n]{3}表示
3
n
\sqrt[n]{3}
n3 |
| \left,\right | 自动匹配合适大小的左右括号()[] |
矩阵写法
$$ ## 公式一定要有
\begin{bmatrix} # 矩阵开始
t_1 & t_2 \\ #用&连接一行的内容,用\\换行
t_3 & t_4
\end{bmatrix} #结束矩阵
$$
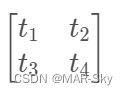
$\begin{matrix} 1 & 2 \\ 3 & 4 \\ \end{matrix}$
$\begin{pmatrix} 1 & 2 \\ 3 & 4 \\ \end{pmatrix}$
$\begin{bmatrix} 1 & 2 \\ 3 & 4 \\ \end{bmatrix}$
$\begin{Bmatrix} 1 & 2 \\ 3 & 4 \\ \end{Bmatrix}$
$\begin{vmatrix} 1 & 2 \\ 3 & 4 \\ \end{vmatrix}$
$\begin{Vmatrix} 1 & 2 \\ 3 & 4 \\ \end{Vmatrix}$
对应如下几种表现形式
1
2
3
4
\begin{matrix} 1 & 2 \\ 3 & 4 \\ \end{matrix}
1324
(
1
2
3
4
)
\begin{pmatrix} 1 & 2 \\ 3 & 4 \\ \end{pmatrix}
(1324)
[
1
2
3
4
]
\begin{bmatrix} 1 & 2 \\ 3 & 4 \\ \end{bmatrix}
[1324]
{
1
2
3
4
}
\begin{Bmatrix} 1 & 2 \\ 3 & 4 \\ \end{Bmatrix}
{1324}
∣
1
2
3
4
∣
\begin{vmatrix} 1 & 2 \\ 3 & 4 \\ \end{vmatrix}
∣∣∣∣1324∣∣∣∣
∥
1
2
3
4
∥
\begin{Vmatrix} 1 & 2 \\ 3 & 4 \\ \end{Vmatrix}
∥∥∥∥1324∥∥∥∥
带分割符的矩阵
$$
\left[
\begin{array}{cc|c}
1 & 2 & 3 \\
4 & 5 & 6 \\
\end{array}
\right]
$$
:'其中{cc|c}表示了矩阵中分割的位置'
[ 1 2 3 4 5 6 ] \left[ \begin{array}{cc|c} 1 & 2 & 3 \\ 4 & 5 & 6 \\ \end{array} \right] [142536]
做表格
$$
\begin{array}{c|lcr}
n & \text{左对齐} & \text{居中对齐} & \text{右对齐} \\
\hline
1 & 0.24 & 1 & 125 \\
2 & -1 & 189 & -8 \\
3 & -20 & 2000 & 1+10i \\
\end{array}
$$
n 左对齐 居中对齐 右对齐 1 0.24 1 125 2 − 1 189 − 8 3 − 20 2000 1 + 10 i \begin{array}{c|lcr} n & \text{左对齐} & \text{居中对齐} & \text{右对齐} \\ \hline 1 & 0.24 & 1 & 125 \\ 2 & -1 & 189 & -8 \\ 3 & -20 & 2000 & 1+10i \\ \end{array} n123左对齐0.24−1−20居中对齐11892000右对齐125−81+10i
条件表达式
$$
f(n) =
\begin{cases}
n/2, & \text{if $n$ is even} \\
3n+1, & \text{if $n$ is odd} \\
\end{cases}
$$
f
(
n
)
=
{
n
/
2
,
if
n
is even
3
n
+
1
,
if
n
is odd
f(n) = \begin{cases} n/2, & \text{if $n$ is even} \\ 3n+1, & \text{if $n$ is odd} \\ \end{cases}
f(n)={n/2,3n+1,if n is evenif n is odd
左侧对齐
$$
\left.
\begin{array}{l}
\text{if $n$ is even:} & n/2 \\
\text{if $n$ is odd:} & 3n+1 \\
\end{array}
\right\}
=f(n)
$$
if n is even: n / 2 if n is odd: 3 n + 1 } = f ( n ) \left. \begin{array}{l} \text{if $n$ is even:} & n/2 \\ \text{if $n$ is odd:} & 3n+1 \\ \end{array} \right\} =f(n) if n is even:if n is odd:n/23n+1}=f(n)
条件表达式行高问题
不适配
$$
f(n) =
\begin{cases}
\frac{n}{2}, & \text{if $n$ is even} \\
3n+1, & \text{if $n$ is odd} \\
\end{cases}
$$
f ( n ) = { n 2 , if n is even 3 n + 1 , if n is odd f(n) = \begin{cases} \frac{n}{2}, & \text{if $n$ is even} \\ 3n+1, & \text{if $n$ is odd} \\ \end{cases} f(n)={2n,3n+1,if n is evenif n is odd
适配行高
$$
f(n) =
\begin{cases}
\frac{n}{2}, & \text{if $n$ is even} \\[2ex]
3n+1, & \text{if $n$ is odd} \\
\end{cases}
$$
f ( n ) = { n 2 , if n is even 3 n + 1 , if n is odd f(n) = \begin{cases} \frac{n}{2}, & \text{if $n$ is even} \\[2ex] 3n+1, & \text{if $n$ is odd} \\ \end{cases} f(n)=⎩⎨⎧2n,3n+1,if n is evenif n is odd
省略符号的矩阵
\cdots对应: ⋯ \cdots ⋯ , \ddots 对应: ⋱ \ddots ⋱ , \vdots : ⋮ \vdots ⋮
累加写法
$$
\sum \limits_{i=1}^nx_i
$$
∑ i = 1 n x i \sum \limits_{i=1}^nx_i i=1∑nxi
分式和公式标号写法
$$
a = \dfrac{d}{b} \tag{1}
$$
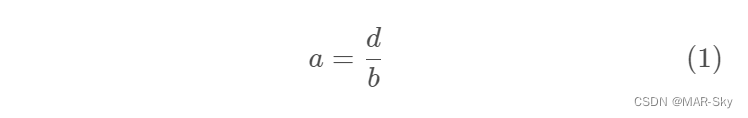
下面这行代码也能达到这个功能
$$
a = {d \over b}
$$
连续分式
$$
x = a_0 + \cfrac{1^2}{a_1 +
\cfrac{2^2}{a_2 +
\cfrac{3^2}{a_3 +
\cfrac{4^4}{a_4 +
\cdots
}
}
}
}
$$
$$
x = a_0 + \frac{1^2}{a_1 +
\frac{2^2}{a_2 +
\frac{3^2}{a_3 +
\frac{4^4}{a_4 +
\cdots
}
}
}
}
$$
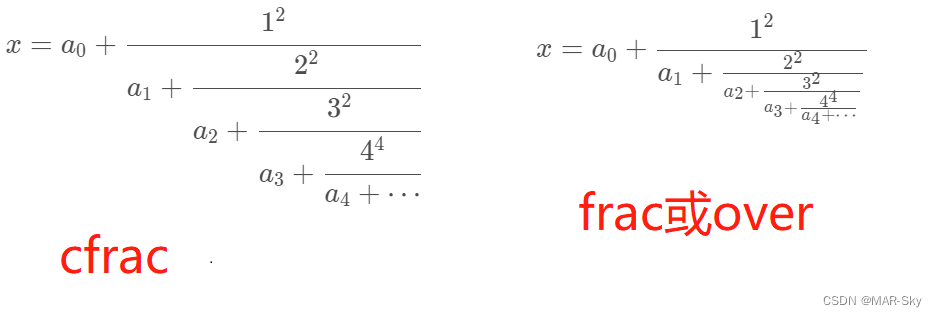
希腊字母和特殊字符
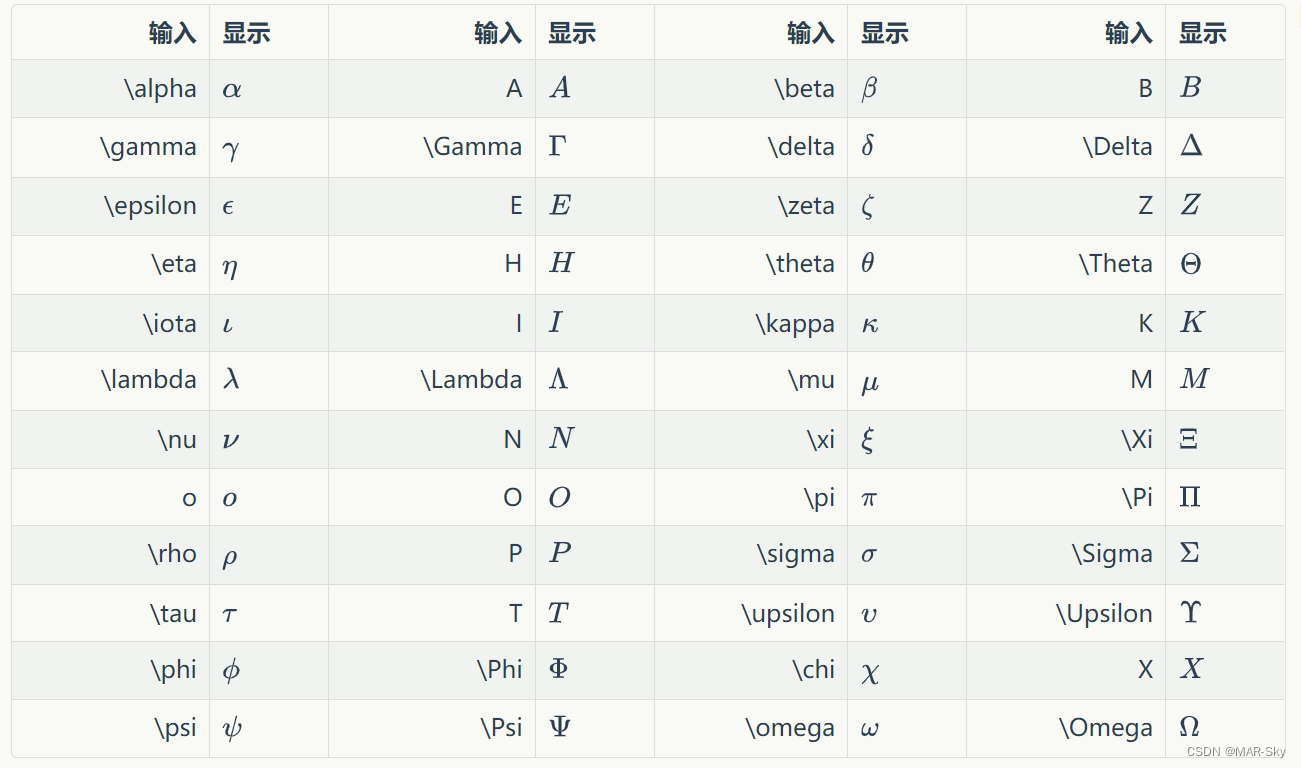
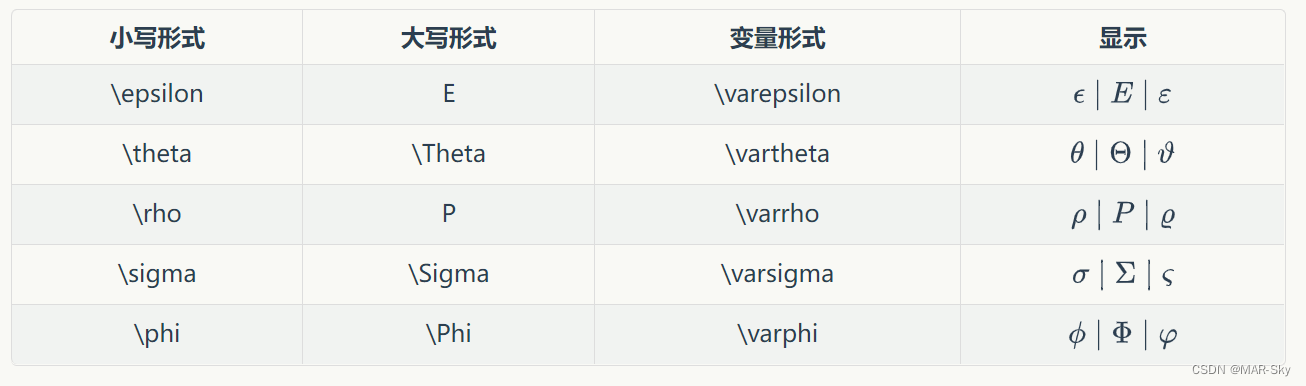
数学符号
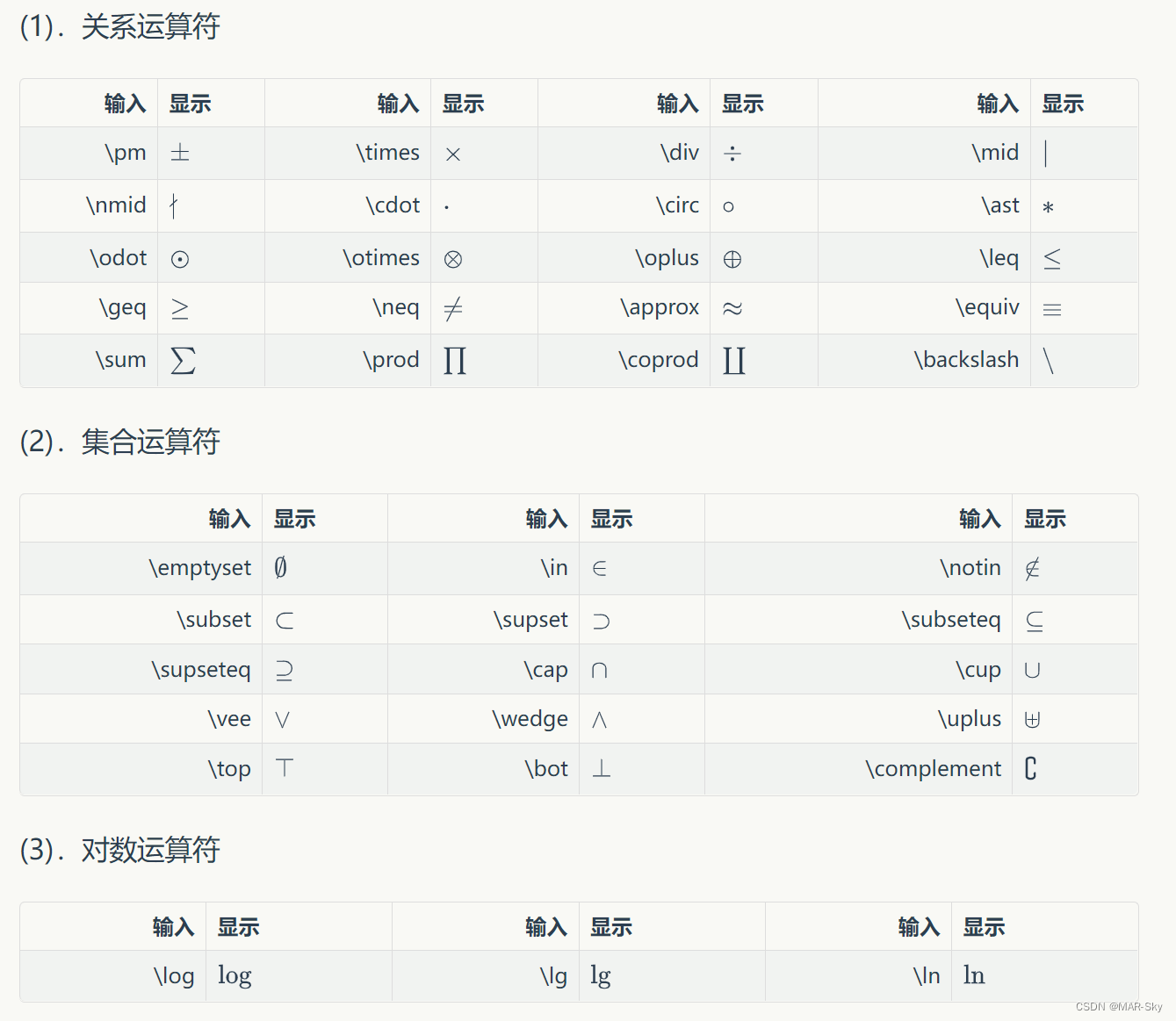
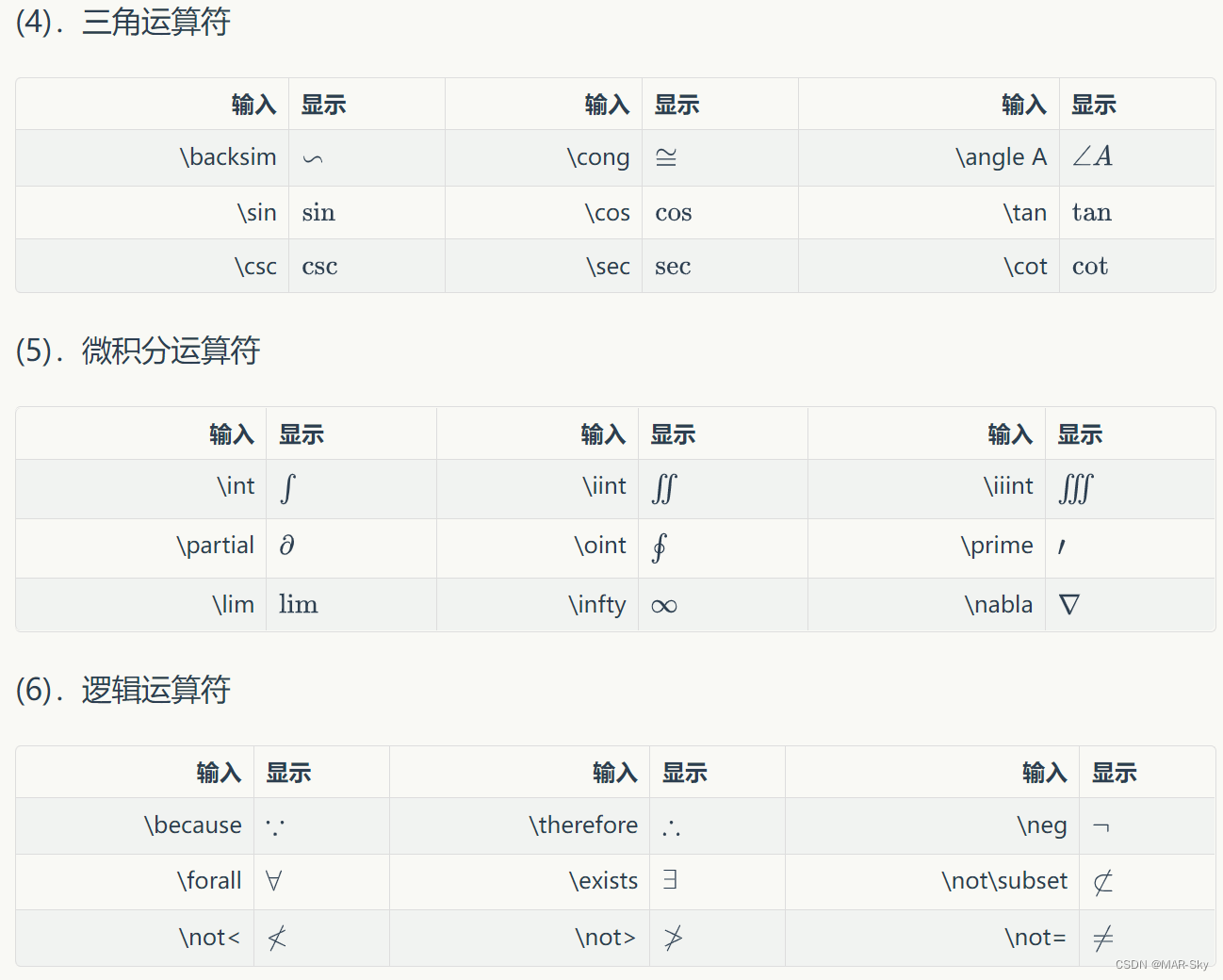
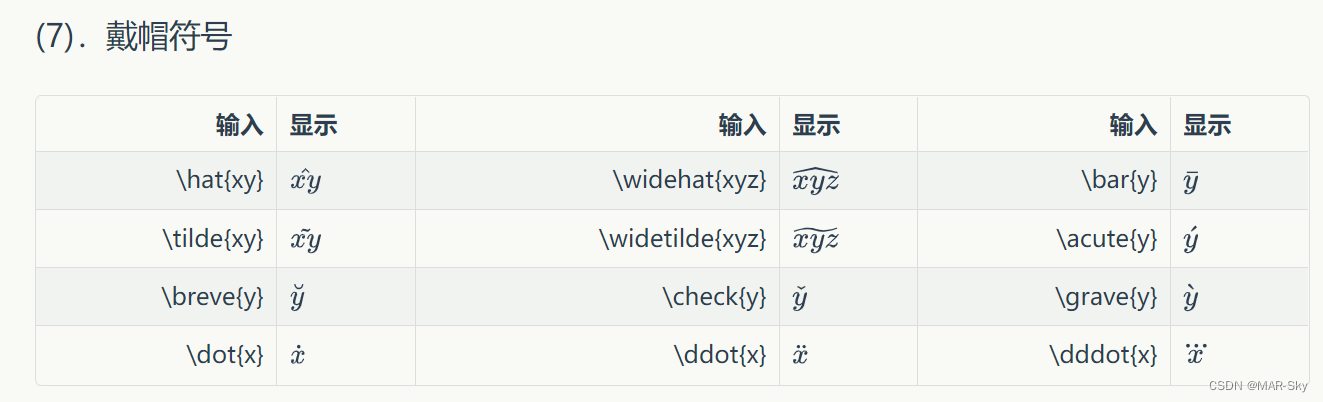
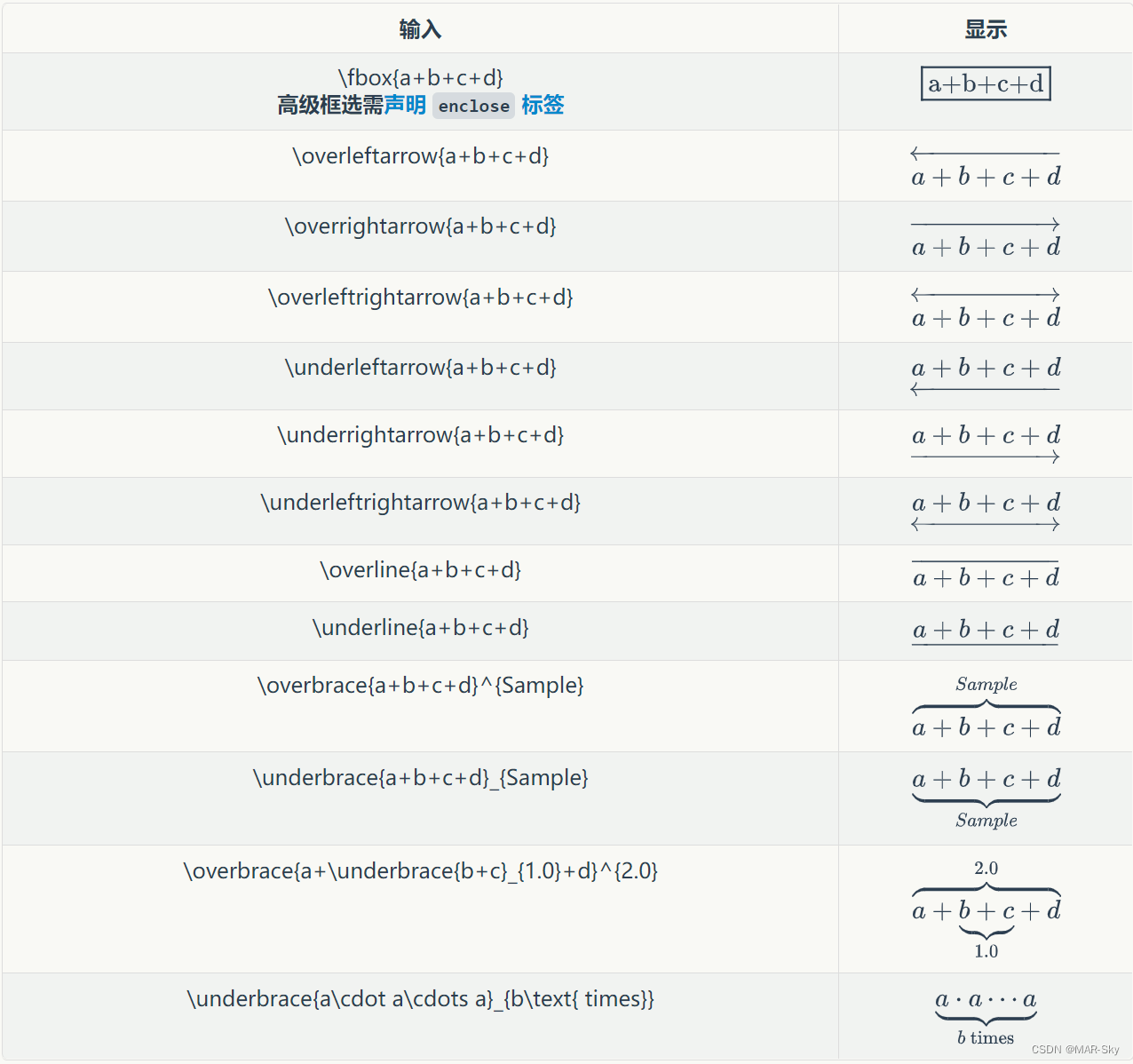
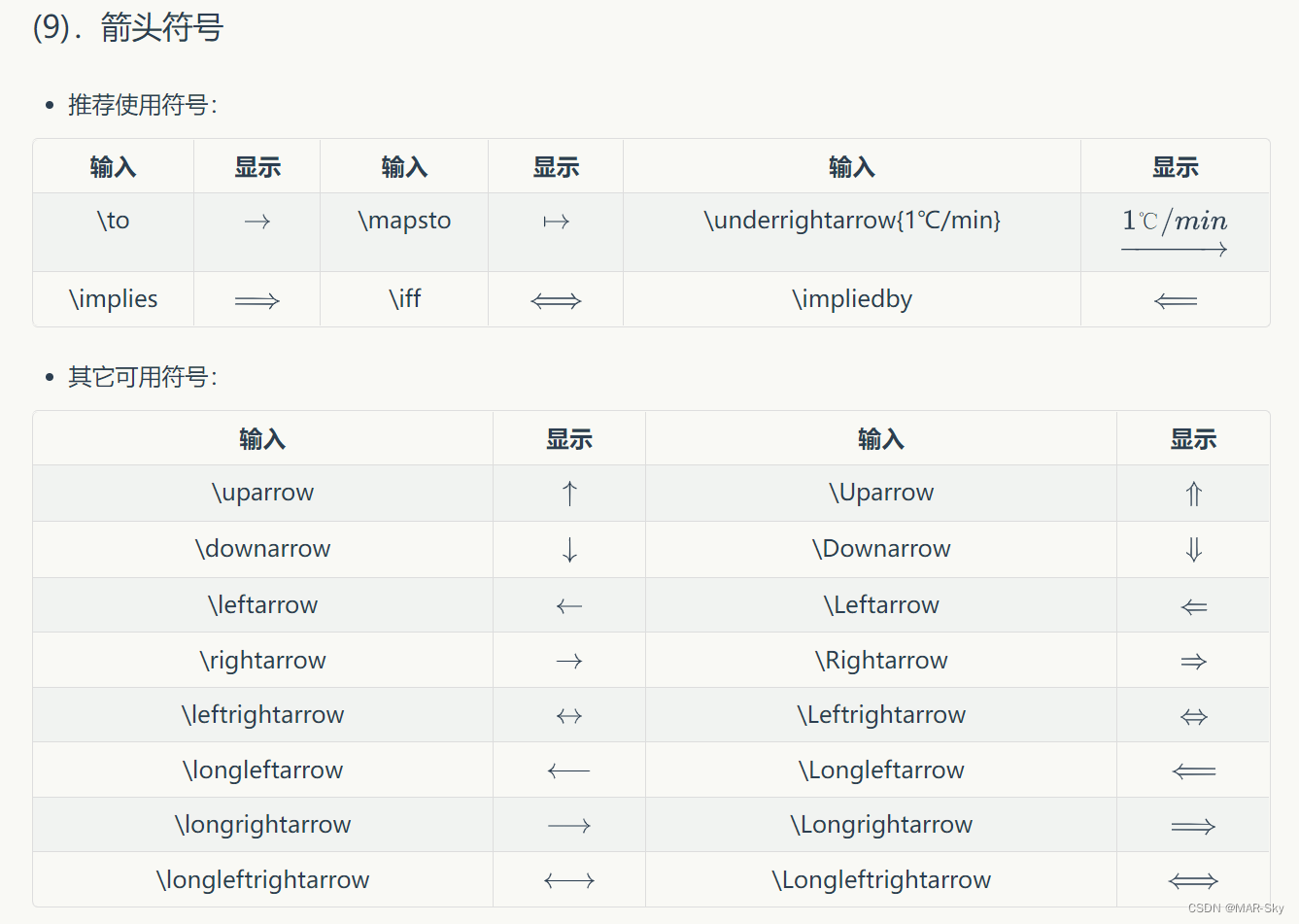
字体修改
使用格式:{\字体{修饰的文字}}
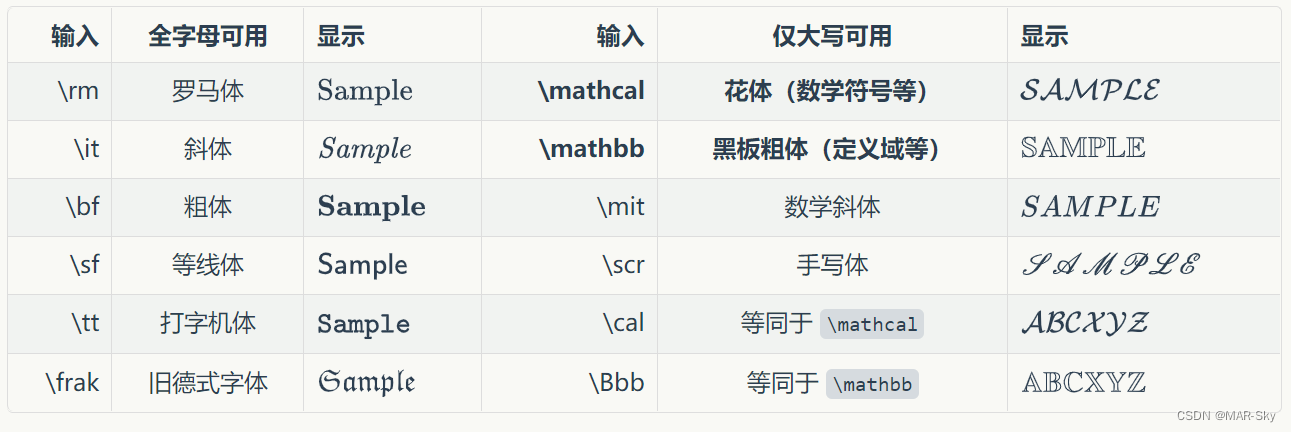
公式高亮,在csdn中貌似不可以
\bbox[底色, (可选)边距, (可选)边框 border: 框宽度 框类型 框颜色]
$$
\bbox[yellow]{
e^x=\lim_{n\to\infty} \left( 1+\frac{x}{n} \right)^n \qquad (1)
}
$$
修改文字颜色
\color{颜色}{文字}
\color {#rgb} {text} 可定义更多颜色
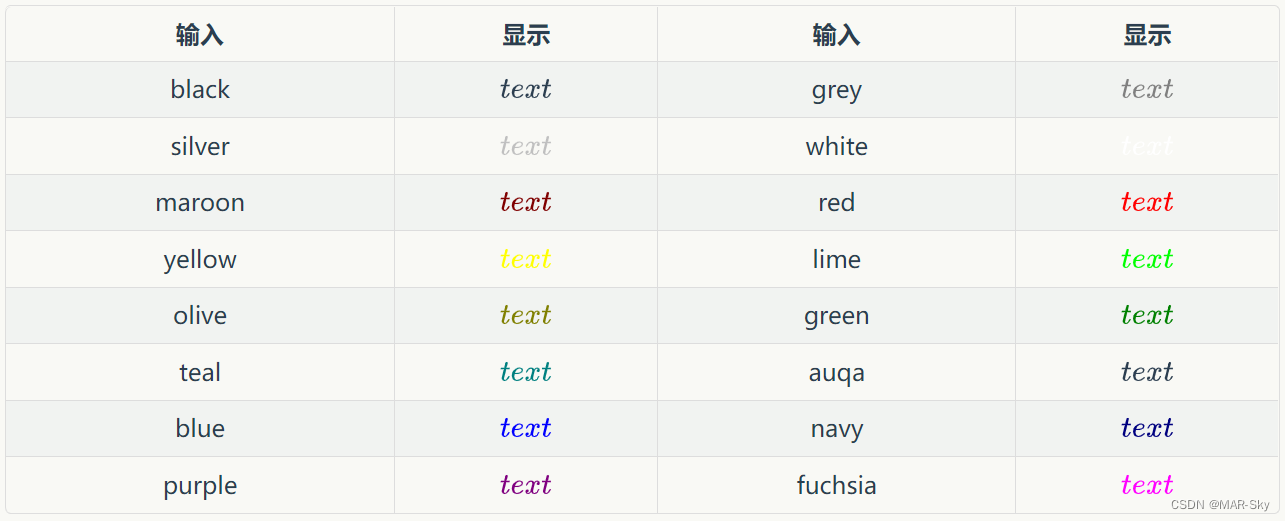
![[附源码]Python计算机毕业设计Django的在线作业批改系统](https://img-blog.csdnimg.cn/267fcf8fc3084e79a41aa353820708c9.png)
![[附源码]Python计算机毕业设计SSM力高灯饰线上交易平台(程序+LW)](https://img-blog.csdnimg.cn/a21e640f09754313922052d17b5efebb.png)



![[附源码]Python计算机毕业设计SSM乐多多宠物店网站(程序+LW)](https://img-blog.csdnimg.cn/6aacf361d5064b61b663f891ad893fd1.png)


![[附源码]Python计算机毕业设计Django的疫苗接种管理系统](https://img-blog.csdnimg.cn/a01b45b9dd50463585ab95d280c2c76f.png)