逆序对
Time Limit: 1000 MS		Memory Limit: 5000 KB

Description

给定一个长度为N的int型数组a[0,1,2,...N-1], 请计算逆序对个数.当i<j且a[i]>a[j], 则称a[i]与a[j]是一对逆序对.

Input

第一行输入M表示包含M组测试数据，每组先输入N (N<=50000), 接着输入N个int型整数.

Output

输出逆序对个数.

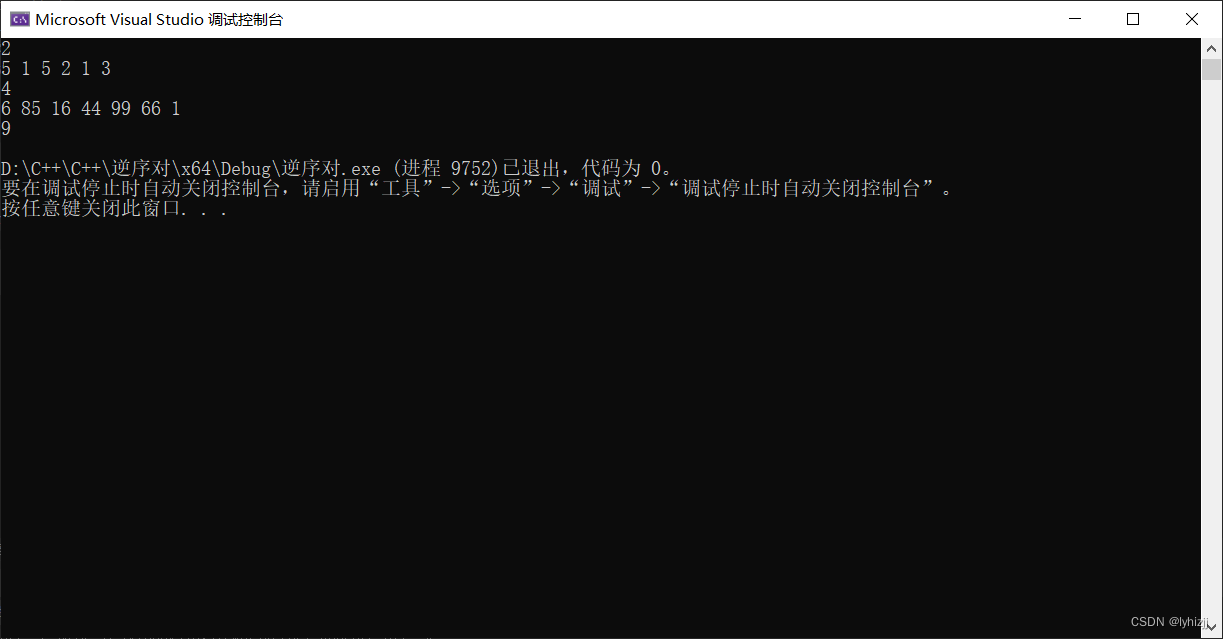
Sample Input

2
5 1 5 2 1 3
6 85 16 44 99 66 1

Sample Output

4
9

解法：

这是一个求解逆序对问题的算法题。可以使用归并排序的思想进行求解。

归并排序的过程中，将两个有序数组合并成一个有序数组的过程中，若右边的元素小于左边的元素，则构成了逆序对。因此，在归并排序的过程中，可以统计逆序对的数量。

具体来说，对于一个数组a，可以将其分为两个子数组left和right，分别对left和right进行归并排序，得到两个有序数组，然后将这两个有序数组合并成一个有序数组，合并过程中统计逆序对的数量。这样就可以得到整个数组的逆序对数量。只需记录交换次数，即为逆序对数量

#include <iostream>
using namespace std;

const int N = 50010;

int a[N], b[N];

long long merge_sort(int l, int r) {
    if (l == r) return 0;  // 当数组长度为1时，逆序对数量为0

    int mid = (l + r) >> 1;  // 将数组分成两个子区间
    long long cnt = merge_sort(l, mid) + merge_sort(mid + 1, r);  // 对子区间递归排序，并计算逆序对数量

    int i = l, j = mid + 1, k = 0;
    while (i <= mid && j <= r) {  // 将两个有序子区间合并成一个有序序列，并统计逆序对数量
        if (a[i] <= a[j]) b[k++] = a[i++];
        else {
            b[k++] = a[j++];
            cnt += mid - i + 1;
        }
    }

    while (i <= mid) b[k++] = a[i++];
    while (j <= r) b[k++] = a[j++];
    for (i = l, j = 0; i <= r; i++, j++) a[i] = b[j];  // 将有序序列存回原数组

    return cnt;  // 返回逆序对数量
}

int main() {
    int T, n;
    cin >> T;
    while (T--) {
        cin >> n;
        for (int i = 0; i < n; i++) cin >> a[i];

        long long cnt = merge_sort(0, n - 1);
        cout << cnt << endl;
    }
    return 0;
}
		
	

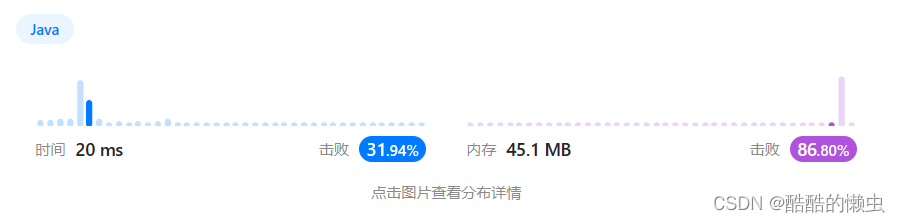
下面是运行结果：