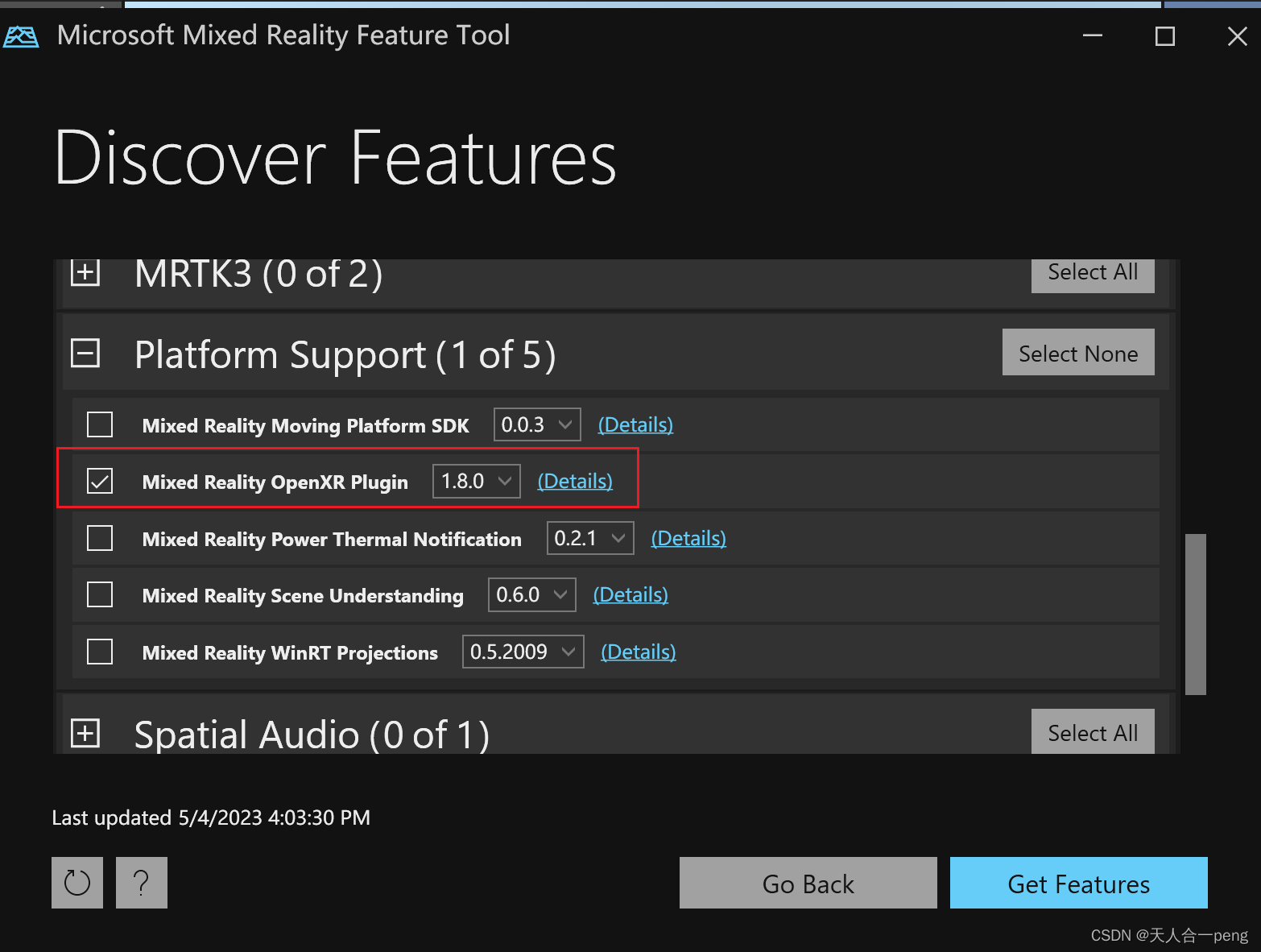
蒟蒻来讲题,还望大家喜。若哪有问题,大家尽可提!
Hello, 大家好哇!本初中生蒟蒻讲解一下Acjudge #P1004. 整除三元组!
===========================================================================================
原题
题目背景
潍坊高新OI社区打算开讲“数论”了,大家赶紧来学习一下“整除”吧。
题目描述
给你两个整数n和m,希望你构造出尽可能多的三元组 ( x , y , z ) (x,y,z) (x,y,z)(注意: x , y , z x,y,z x,y,z是小于等于 n n n的正整数)。 使得三元组中的 x + y , x + z , y + z x+y, x+z, y+z x+y,x+z,y+z都能够被 m m m整除,一共有多少满足题意的三元组呢?
注意:顺序不同的三元组,是不同的方案排列
数据格式
输入格式
一行共两个整数n和m.
输出格式
输出一个整数, 表示满足条件的方案数
思路
根据
x
+
y
,
x
+
z
,
y
+
z
x+y, x+z, y+z
x+y,x+z,y+z都能够被
m
m
m整除
我们可以得出
x
≡
y
≡
z
(
m
o
d
x\equiv y\equiv z(mod
x≡y≡z(mod
m
)
m)
m)
得出条件:
- x ≡ y ≡ z ( m o d x\equiv y\equiv z(mod x≡y≡z(mod m ) m) m)
- x , y , z ≤ n x, y, z\le n x,y,z≤n
两种情况:
情况一(A级):
x
,
y
,
z
x, y, z
x,y,z均为m的倍数
此时
x
,
y
,
z
x,y,z
x,y,z可以取得数的个数为
⌊
n
m
⌋
\left \lfloor \frac{n}{m} \right \rfloor
⌊mn⌋,所以通过乘法原理得此时的方案数就是
⌊
n
m
⌋
3
\left \lfloor \frac{n}{m} \right \rfloor^3
⌊mn⌋3
情况二(A级):
x
,
y
,
z
x,y,z
x,y,z都不是m的倍数
注:不可能
(
x
,
y
,
z
)
(x,y,z)
(x,y,z)中若干个是m的倍数,其余的不是,因为我们的大前提:
x
≡
y
≡
z
(
m
o
d
x\equiv y\equiv z(mod
x≡y≡z(mod
m
)
m)
m)
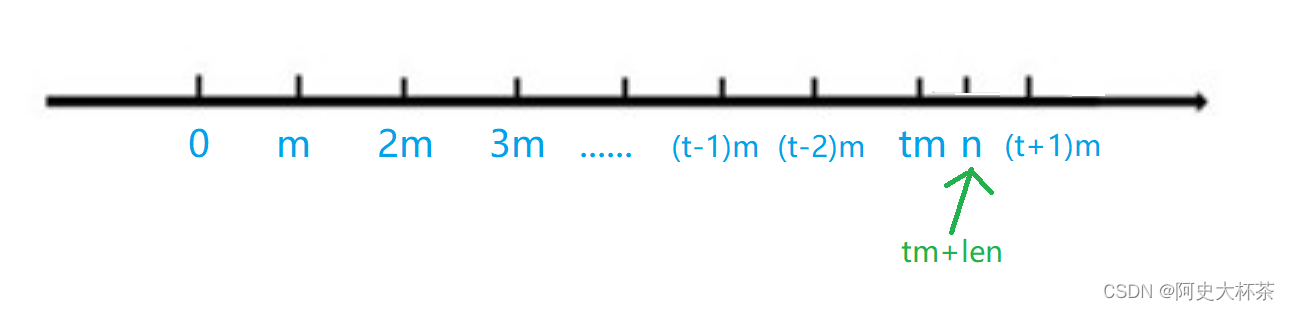
此时,设 t = ⌊ n m ⌋ t=\left \lfloor \frac{n}{m} \right \rfloor t=⌊mn⌋,我们把 0 − n 0-n 0−n划分成若干个长度为 m m m的区域
这时候,又分了两种情况:
情况一(B级):
n
%
m
!
=
0
n\% m!=0
n%m!=0(如图)

我们会发现,选择的区域多了一块,长度为
n
%
m
n\%m
n%m,这一块一定可以选吗?
又又又分出了两种情况:
设
l
e
n
=
n
%
m
len=n\%m
len=n%m
情况一(C级):
x
%
m
,
y
%
m
,
z
%
m
≤
l
e
n
x\%m,y\%m,z\%m\le len
x%m,y%m,z%m≤len
此时我们发现选择的区域有
t
+
1
t+1
t+1个了,此时的方案数就是
(
⌊
n
m
⌋
+
1
)
3
(\left \lfloor \frac{n}{m} \right \rfloor+1)^3
(⌊mn⌋+1)3
情况二(C级):
x
%
m
,
y
%
m
,
z
%
m
≥
l
e
n
x\%m,y\%m,z\%m\ge len
x%m,y%m,z%m≥len
此时对于
t
m
−
n
tm-n
tm−n这一段区间肯定是选择不到的,因为
l
e
n
=
n
%
m
len=n\%m
len=n%m,而
x
%
m
,
y
%
m
,
z
%
m
≥
l
e
n
x\%m,y\%m,z\%m\ge len
x%m,y%m,z%m≥len若
x
,
y
,
z
x,y,z
x,y,z在
t
m
−
(
t
+
1
)
m
tm-(t+1)m
tm−(t+1)m区间内,一定就在
n
n
n的右边,就不符合
x
,
y
,
z
≤
n
x, y, z\le n
x,y,z≤n这个条件了!
所以,此时的方案数就是
⌊
n
m
⌋
3
\left \lfloor \frac{n}{m} \right \rfloor^3
⌊mn⌋3
然后,我们看一下
x
%
m
,
y
%
m
,
z
%
m
≤
l
e
n
x\%m,y\%m,z\%m\le len
x%m,y%m,z%m≤len等于多少,基于
x
≡
y
≡
z
(
m
o
d
x\equiv y\equiv z(mod
x≡y≡z(mod
m
)
m)
m),他们都是相等的,考虑其中一个即可,这里我们设
a
=
x
%
m
a=x\%m
a=x%m
我们利用一下题目中给的条件:
(
x
+
y
)
%
m
=
0
(x+y)\%m=0
(x+y)%m=0
再利用模的性质(可以看看这篇文章)得:
(
x
%
m
+
y
%
m
)
%
m
=
0
(x\%m+y\%m)\%m=0
(x%m+y%m)%m=0,即:
2
a
%
m
=
0
2a\%m=0
2a%m=0
由于
a
<
m
a<m
a<m,所以
2
a
<
2
m
2a<2m
2a<2m
故,有两种解:
2
a
=
m
或
2
a
=
0
2a=m或2a=0
2a=m或2a=0
对于
2
a
=
0
2a=0
2a=0,即
a
=
0
a=0
a=0:就是情况一(A级)
对于
2
a
=
m
2a=m
2a=m,即
a
=
m
2
a=\frac{m}{2}
a=2m:此时我们解出了a,也就是
x
%
m
=
m
2
x\%m=\frac{m}{2}
x%m=2m,而m是已知的,所以就可以代入求得是哪一种情况了!
不过,我们发现一个问题!
x
,
y
,
z
x,y,z
x,y,z是整数,那么
x
%
m
x\%m
x%m也一定是整数,可是
m
2
\frac{m}{2}
2m有可能是小数,所以对于
m
m
m不是2的倍数时,情况2(A级)不成立!
情况二(B级):

这时候,很简单,还是
t
t
t块,所以此时的方案数就是
⌊
n
m
⌋
3
\left \lfloor \frac{n}{m} \right \rfloor^3
⌊mn⌋3
前面出现了不成立的情况,所以总结一下:
- 若
m
m
m不是2的倍数
答案为: ⌊ n m ⌋ 3 \left \lfloor \frac{n}{m} \right \rfloor^3 ⌊mn⌋3 - 若
m
m
m是2的倍数
(1) n % m = 0 n\%m=0 n%m=0 答案为: 2 ⌊ n m ⌋ 3 2\left \lfloor \frac{n}{m} \right \rfloor^3 2⌊mn⌋3
(2) n % m ! = 0 n\%m!=0 n%m!=0
\qquad ① m 2 > n % m \frac{m}{2}>n\%m 2m>n%m 答案为: 2 ⌊ n m ⌋ 3 2\left \lfloor \frac{n}{m} \right \rfloor^3 2⌊mn⌋3
\qquad ② m 2 ≤ n % m \frac{m}{2}\le n\%m 2m≤n%m 答案为: ⌊ n m ⌋ 3 + ( ⌊ n m ⌋ + 1 ) 3 \left \lfloor \frac{n}{m} \right \rfloor^3+(\left \lfloor \frac{n}{m} \right \rfloor+1)^3 ⌊mn⌋3+(⌊mn⌋+1)3
代码
#include <iostream>
#define int long long
using namespace std;
int n, m;
signed main()
{
cin >> n >> m;
int res = 0;
int cnt = n / m;
res += cnt * cnt * cnt;
if (!(m & 1))
if (n % m == 0)
res += cnt * cnt * cnt;
else
{
int q = n % m;
if (m / 2 <= q)
res += (cnt + 1) * (cnt + 1) * (cnt + 1);
else
res += cnt * cnt * cnt;
}
cout << res << endl;
}
今天就到这里了!
大家有什么问题尽管提,我都会尽力回答的!
吾欲您伸手,点的小赞赞。吾欲您喜欢,点得小关注!