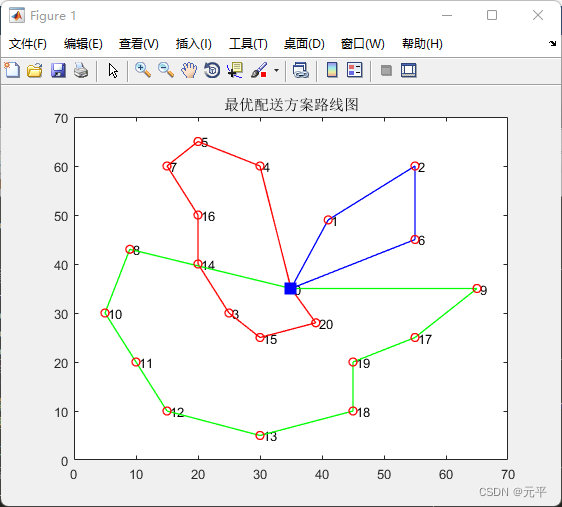
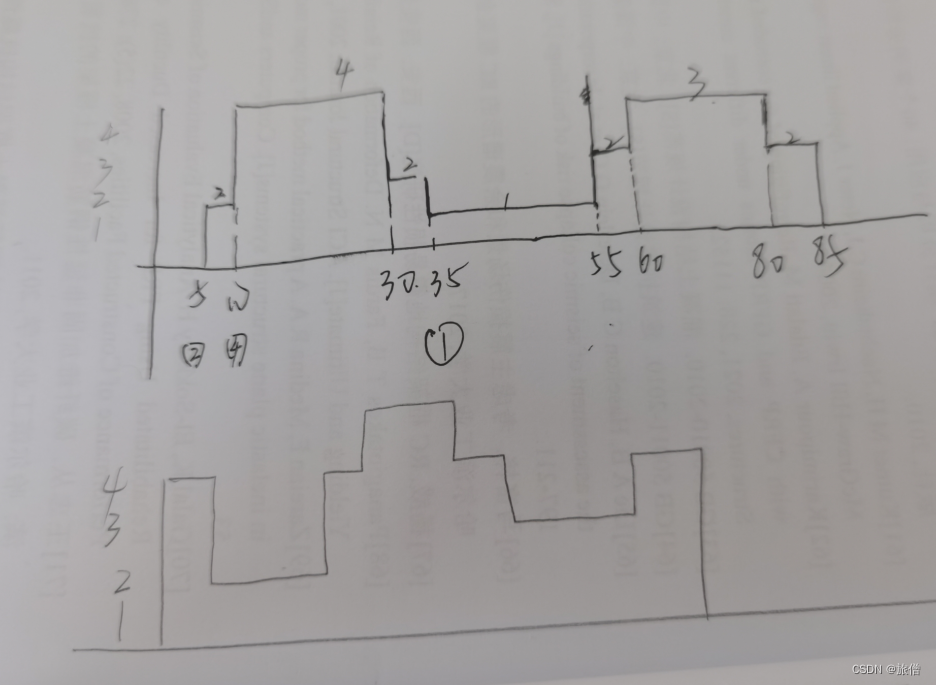
车辆配送路径优化问题可描述为：某商超配送中心要使用一定数量的车辆对一批货物进行配送服务，要求在不超过车辆的额定载重量和额定容积的条件下，安排这些货物的装载，使得车辆利用率最高。
针对以上问题做出假设：
(1) 只有一个配送中心，所有车辆都是从配送中心出发并最终回到配送中心；
(2) 配送中心和客户站点的具体位置已知；
(3) 配送车辆的类型相同，装载容量大小已知；
(4) 配送车辆的最大实际装载货物重量不能超过货车的最大承载重量；
(5) 配送车辆匀速行驶；
(6) 每个客户站点的需求量已知；
(7) 每条配送路线只能由一辆配送车辆进行配送，且每个站点只能被配送一次；
(8) 不考虑交通堵塞或不可通行的情况。
数学模型
模型中的数学符号决策变量描述
k 为车辆编号，k=1,2,…,l;
i,j 表示客户编号，i,j=0,1,2,…,n, i,j=0表示配送中心；
p 为货物编号，p=1,2,…,m;
Gk为车辆 k 的最大载重量；
Vk 为车辆 k 的最大容积;
g ip为货物 p 的重量；
Vip货物 p 的体积，且货物尺寸均小于货车车厢尺寸;
模型的约束条件限制：



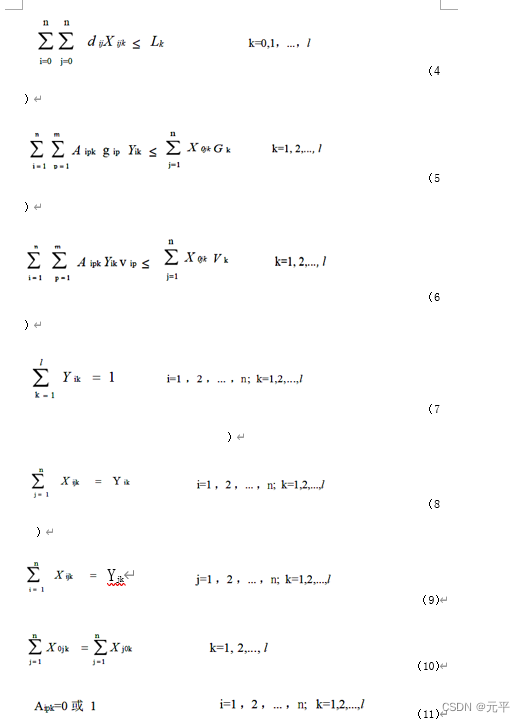
目标函数处理：



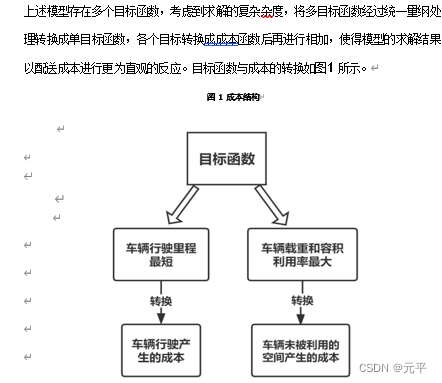
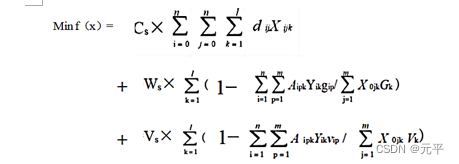
算法仿真：
数据如下所示：

使用蚁群算法，matlab求解如下：

tic
clear
clc
%% 用importdata这个函数来读取文件 
dataset=importdata('input_test.txt'); %读取输入数据文件
%cap=200;
cap = 3000;
Rated_volume = 20;

%% 提取数据信息
vertexs=dataset(:,2:3);                                         %所有点的坐标x和y
customer=vertexs(2:end,:);                                      %顾客坐标
cusnum=size(customer,1);                                        %顾客数
demands=dataset(2:end,4);                                       %需求量
Tj_demands = dataset(2:end,5);                                  %体积需求
Cs = 2;
Ws = 50;
Vs = 0.06;
h=pdist(vertexs);
dist=squareform(h);                                             %成本矩阵即任意两点之间的距离
%% 初始化参数
m=50;                                                           %蚂蚁数量
alpha=1;                                                        %信息素重要程度因子
beta=5;                                                         %启发函数重要程度因子
rho=0.85;                                                       %信息素挥发因子
Q=5;                                                            %更新信息素浓度的常数
Eta=1./dist;                                                    %启发函数
Tau=ones(cusnum+1,cusnum+1);                                    %信息素矩阵
Table=zeros(m,cusnum);                                          %路径记录表
iter=1;                                                         %迭代次数初值
iter_max=100;                                                   %最大迭代次数
Route_best=zeros(iter_max,cusnum);                              %各代最佳路径
Cost_best=zeros(iter_max,1);                                    %各代最佳路径的成本
%% 迭代寻找最佳路径
while iter<=iter_max
    %% 先构建出所有蚂蚁的路径
    %逐个蚂蚁选择
    for i=1:m
        %逐个顾客选择
        for j=1:cusnum
            np = next_point(i,Table,Tau,Eta,alpha,beta,dist,cap,demands,Tj_demands,Rated_volume);
            Table(i,j)=np;
        end
    end
    %% 计算各个蚂蚁的成本
    cost=zeros(m,1);
    NV=zeros(m,1);
    TD=zeros(m,1);
    for i=1:m
        VC = decode(Table(i,:),cap,demands,dist,Tj_demands,Rated_volume);
        [cost(i,1),NV(i,1),TD(i,1)] = MulticostFun(VC,dist,demands,cap,Tj_demands,Rated_volume,Cs,Ws,Vs);
    end
    %% 计算最小成本及平均成本
    if iter == 1
        [min_Cost,min_index]=min(cost);
        Cost_best(iter)=min_Cost;
        Route_best(iter,:)=Table(min_index,:);
    else
        [min_Cost,min_index]=min(cost);
        Cost_best(iter)=min(Cost_best(iter - 1),min_Cost);
        if Cost_best(iter)==min_Cost
            Route_best(iter,:)=Table(min_index,:);
        else
            Route_best(iter,:)=Route_best((iter-1),:);
        end
    end
    %% 更新信息素
    bestR=Route_best(iter,:);
    [bestVC,bestNV,bestTD]=decode(bestR,cap,demands,dist,Tj_demands,Rated_volume);
    zz = decode_zz(bestR,cap,demands,dist,Tj_demands,Rated_volume);
    Tau=updateTau(Tau,bestR,rho,Q,cap,demands,dist,Tj_demands,Rated_volume);
    %% 打印当前最优解
    disp(['第',num2str(iter),'代最优解:'])
    disp(['车辆使用数目：',num2str(bestNV),'，车辆行驶总距离：',num2str(bestTD),',最小成本：',num2str(min_Cost)]);
    disp('车辆载重体积：');
    disp(zz(:,1));
    fprintf('\n')
    %% 迭代次数加1，清空路径记录表
    iter=iter+1;
    Table=zeros(m,cusnum);
end
%% 结果显示
bestRoute=Route_best(end,:);
[bestVC,bestNV,bestTD]=decode(bestRoute,cap,demands,dist,Tj_demands,Rated_volume);
draw_Best(bestVC,vertexs);