被控对象

考虑这么一个被控对象
$$J\ddot{\theta }(t)=u(t)+d(t)$$
其中，$J$ 为转动惯量，$\theta$ 为角度，$u$ 为控制量，$d$ 为扰动，且 $d(t)<D$ 扰动有界

设计滑模面

设计滑模面为
$$s=ce(t)+\dot{e}(t)$$
其中跟踪误差及其导数为，${\theta }_d$ 为理想的角度信号
$$e(t)=\theta (t)-{\theta }_d(t)$$

$$\dot{e}(t)=\dot{\theta }(t)-{\dot{\theta }}_d(t)$$

获得控制量

$$\begin{array}{rl}\dot{s}& =c\dot{e}(t)+\ddot{e}(t)=c\dot{e}(t)+\frac{1}{J}(u(t)+d(t))-{\ddot{\theta }}_d(t)=-\epsilon sgn(s)\end{array}$$

反解出控制量$u(t)$
$$u(t)=J(-c\dot{e}(t)+{\ddot{\theta }}_d(t)-\epsilon sgn(s))-d(t)$$
这里我们忽略干扰
$$u(t)=J(-c\dot{e}(t)+{\ddot{\theta }}_d(t)-\epsilon sgn(s))$$

证明稳定性

设LYapunov函数$V=\frac{1}{2}{S}^2$，则有
$$\begin{array}{rl}\dot{V}& =s\dot{s}\\ & =s(c\dot{e}(t)+\ddot{e}(t))\\ & =s(c\dot{e}(t)+\frac{1}{J}(u(t)+d(t))-{\ddot{\theta }}_d(t))\\ & =s(c\dot{e}(t)+\frac{1}{J}(J(-c\dot{e}(t)+{\ddot{\theta }}_d(t)-\epsilon sgn(s))+d(t))-{\ddot{\theta }}_d(t))\\ & =s(-\epsilon sgn(s)+\frac{1}{J}d(t))\\ & =-\epsilon |s|+\frac{1}{J}sd(t)\end{array}$$
可见，当干扰$d(t) $ 有上界时，即 $d(t)<D$ 扰动有界，若$\epsilon$ 取值合理，则系统稳定。

python仿真程序

假设我们跟踪的仿真信号为 ${\theta }_d(t)=sin(t)$ ，转动惯量 $J=10$ ，初始值 $\theta (0)=0$ ，$\dot{\theta }(0)=0$。

import numpy as np
import matplotlib.pyplot as plt

# 被控对象
class ControlModel():
    def __init__(self):
        self.T = 10
        self.times = 10 * 1000
        self.time_T = self.T / self.times

        self.pos = 0

        self.theta = np.zeros(self.times, dtype='float64')
        self.dot_theta = np.zeros(self.times, dtype='float64')
        self.u = np.zeros(self.times, dtype='float64')
        self.d = np.zeros(self.times, dtype='float64')
        self.J = 10

        self.Max_u = 30

    def reset(self):
        self.pos = 0
        self.dot_theta[0] = np.deg2rad(0)
        self.theta[0] = np.deg2rad(0)
        self.d[0] = 0

    def step(self, u):
        if self.pos >= self.times:
            return True

        if np.abs(u) > self.Max_u:
            u = np.sign(u) * self.Max_u

        self.u[self.pos] = u
        self.d[self.pos] = 10
        self.stepOnce()
        self.pos += 1

        return False

    def stepOnce(self):
        data = np.array([self.u[self.pos],
                         self.d[self.pos],
                         self.dot_theta[self.pos],
                         self.theta[self.pos],
                         self.J])

        k1 = self.time_T * self.iterateOnce(data)
        k2 = self.time_T * self.iterateOnce(data + 0.5 * k1)
        k3 = self.time_T * self.iterateOnce(data + 0.5 * k2)
        k4 = self.time_T * self.iterateOnce(data + k3)

        data = data + (k1 + 2 * k2 + 2 * k3 + k4) / 6

        self.dot_theta[self.pos + 1] = data[2]
        self.theta[self.pos + 1] = data[3]

    def iterateOnce(self, data):
        u = data[0]
        d = data[1]
        dot_theta = data[2]
        theta = data[3]
        J = data[4]

        _dot_theta = (u + d) / J
        _theta = dot_theta

        return np.array([0, 0, _dot_theta, _theta, 0])

    def get_theta(self):
        return self.theta[self.pos - 1]

    def get_dot_theta(self):
        return self.dot_theta[self.pos - 1]

# 误差，误差的一阶导，误差的二阶导的结构
class Control:
    def __init__(self):
        self.e = 0
        self.dot_e = 0
        self.ddot_e = 0

    def insert(self, e):
        self.ddot_e = e - self.e - self.dot_e
        self.dot_e = e - self.e
        self.e = e

    def get_e(self):
        return self.e

    def get_dot_e(self):
        return self.dot_e

    def get_ddot_e(self):
        return self.ddot_e

# 生成控制对象
M = ControlModel()
M.reset()
C = Control()
T = Control()

theta_list = []
for i in range(M.times - 1):
    theta_d = np.sin(i / 1000)
    theta_list.append(theta_d)
    e = (theta_d - M.get_theta()) / M.time_T
    C.insert(e)
    T.insert(theta_d)

    c = 5
    varesplion = 3
    s = c * C.get_e() + C.get_dot_e()
    u = M.J * (c * C.get_dot_e() + T.get_ddot_e() + varesplion * np.sign(s))

    M.step(u)

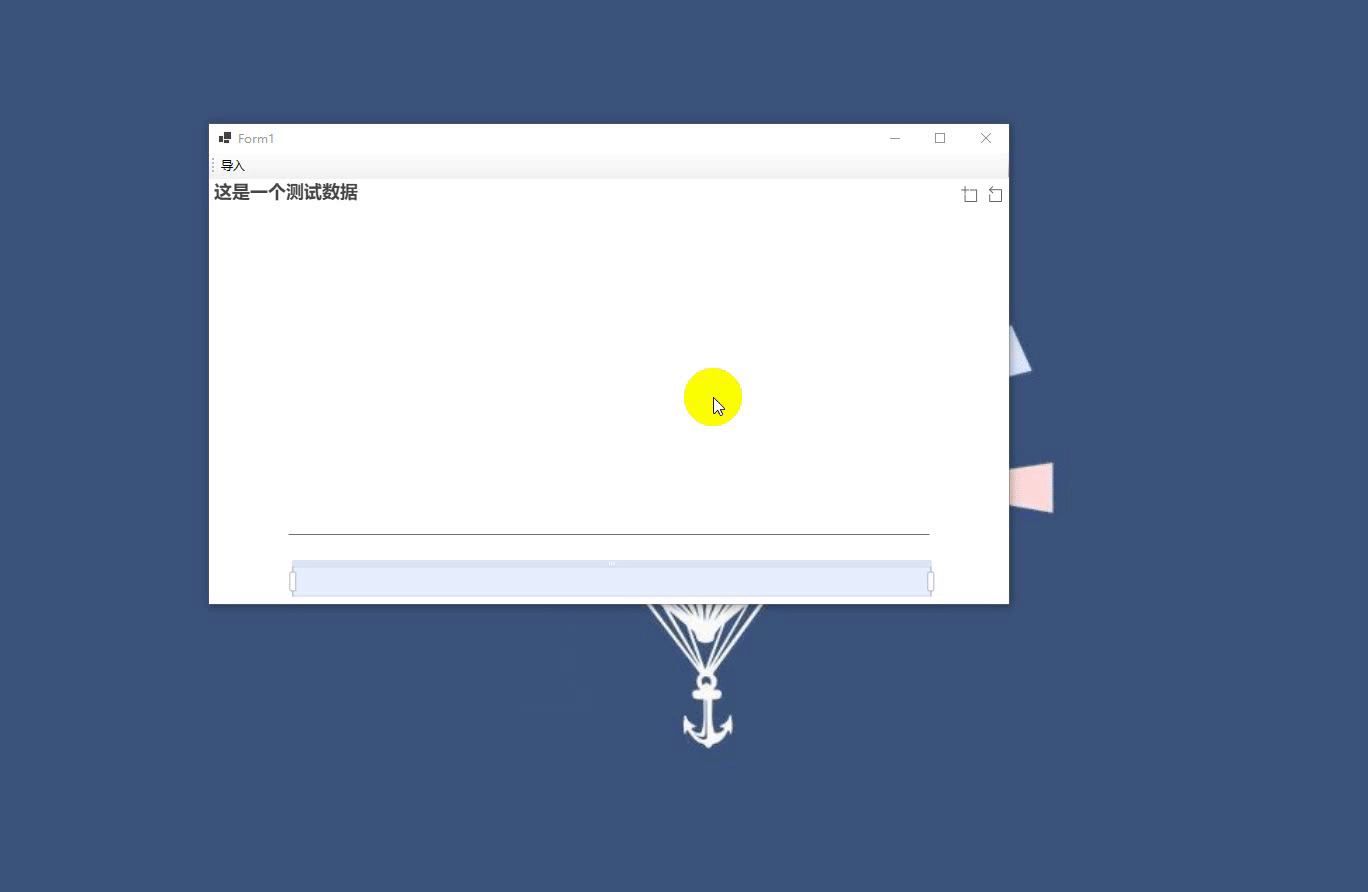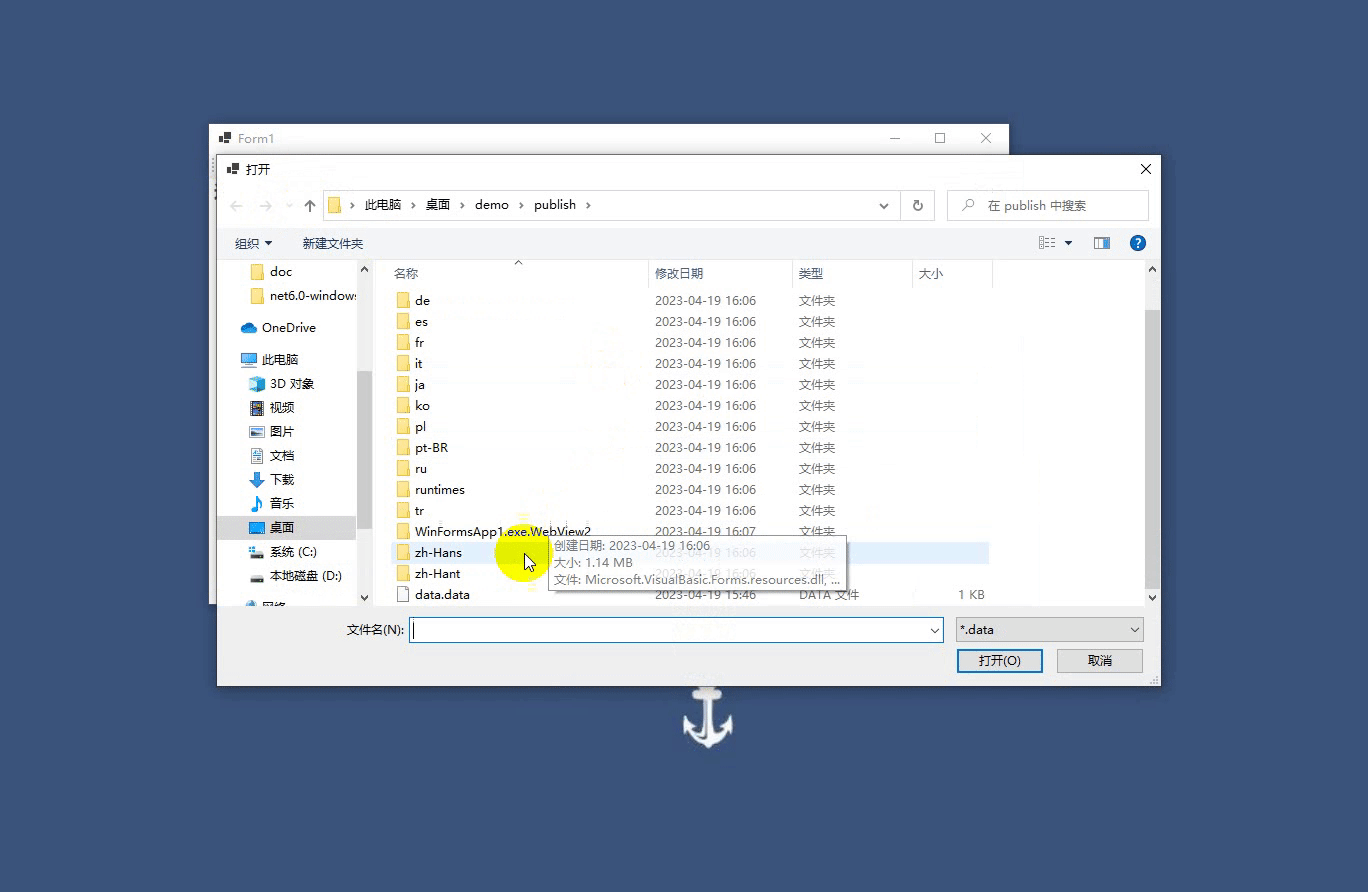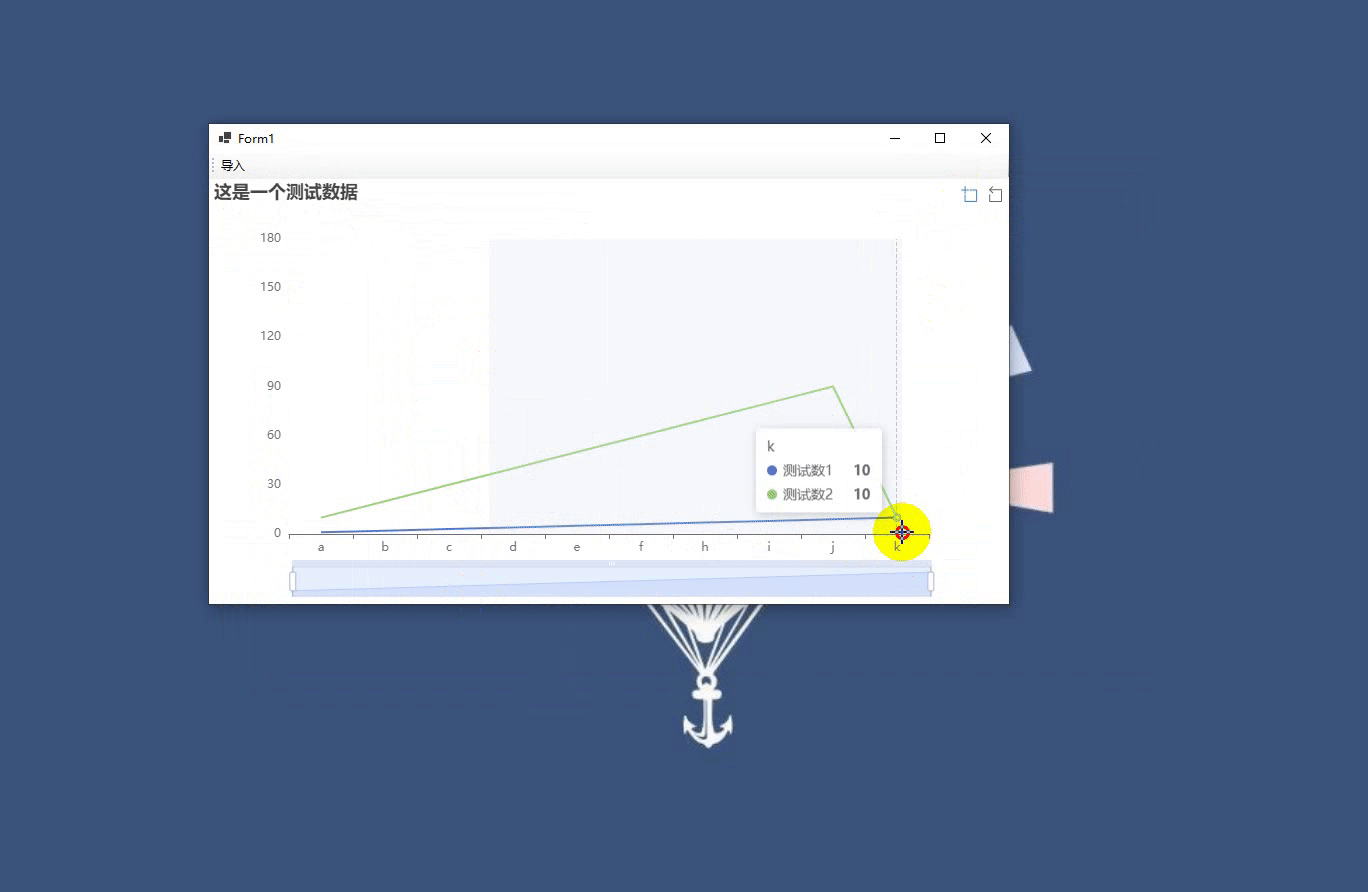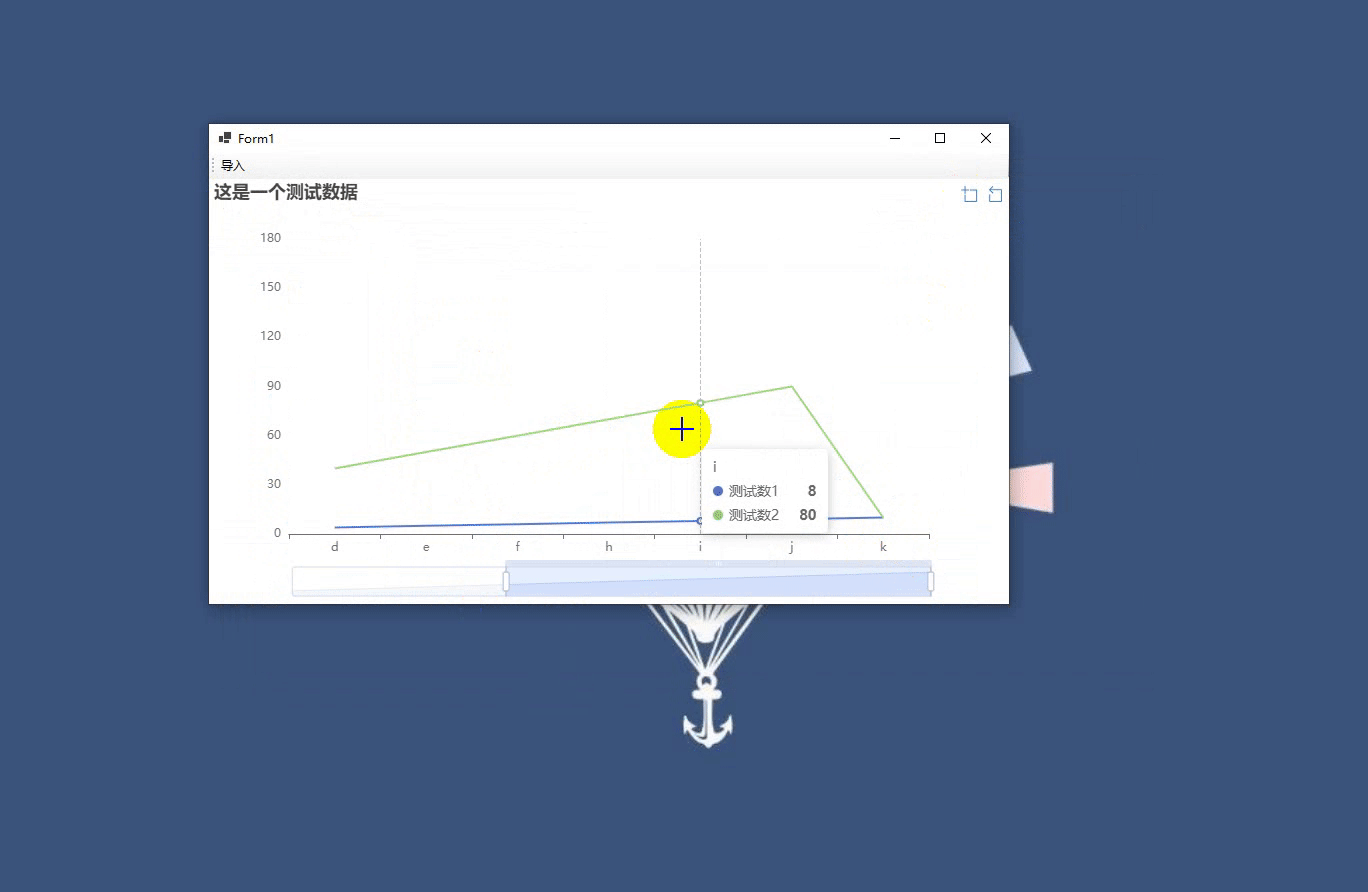
仿真结果

位置跟踪曲线如下

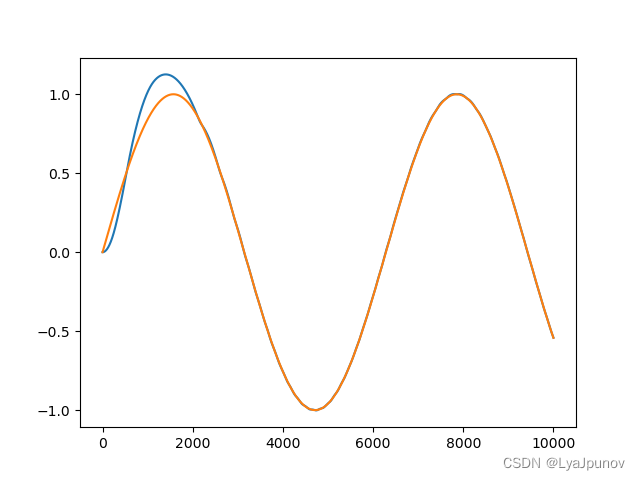
控制量曲线如下

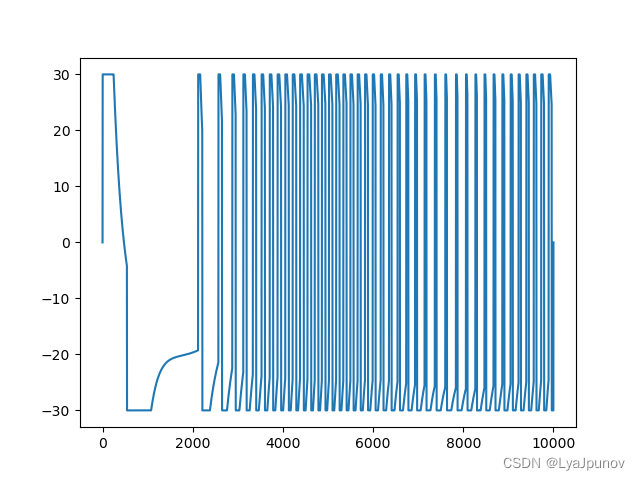
可见，位置跟踪的效果还是不错的，这里我们进行了一定的限幅，限幅影响了它的控制效果，但是控制量是存在抖振的，在真实的控制环境中，元器件不一定承受的起这种抖振。