单词搜索I II/前缀树

news2024/9/28 1:16:30

79单词搜索

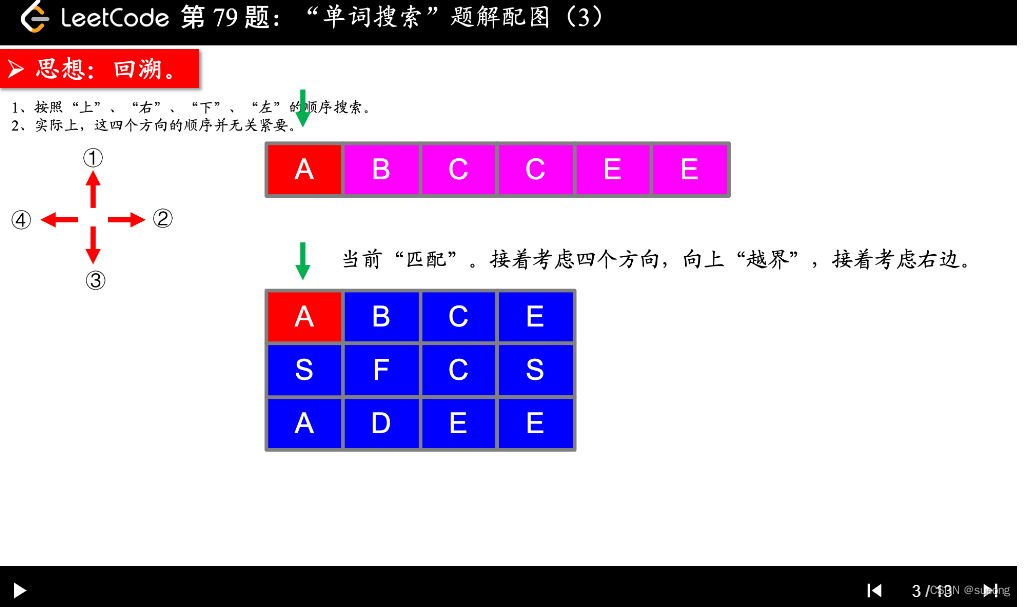
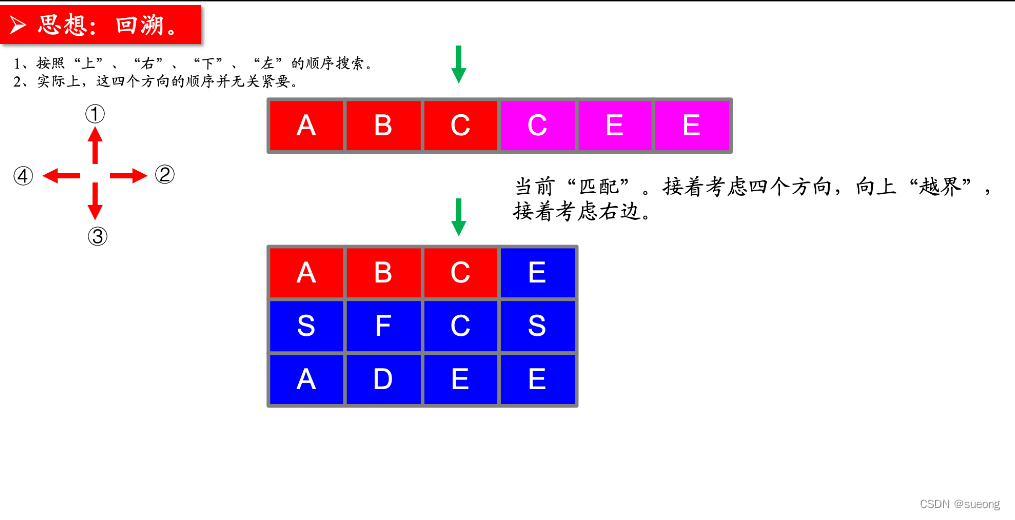
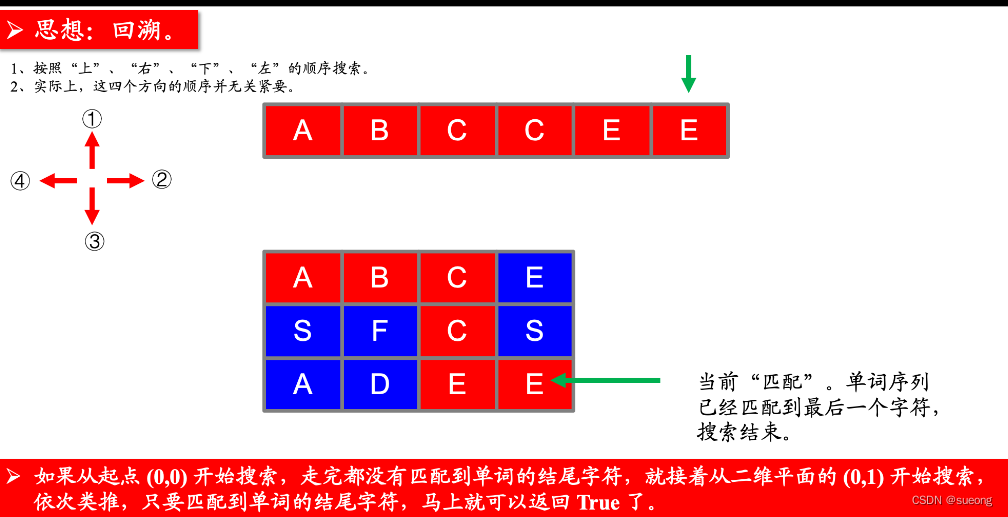
在这里插入图片描述

思路：
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

注意：
我自己在写

for i in range(m):
    for j in range(n):
        # 对每一个格子都从头开始搜索
        if self.__search_word(board, word, 0, i, j, marked, m, n):
            return True

这一段的时候，就写成了：

这一段代码是错误的，不要模仿

for i in range(m):
    for j in range(n):
        # 对每一个格子都从头开始搜索
        return self.__search_word(board, word, 0, i, j, marked, m, n)

这样其实就变成只从坐标 (0,0) 开始搜索，搜索不到返回 False，但题目的意思是：只要你的搜索返回 True 才返回，如果全部的格子都搜索完了以后，都返回 False ，才返回 False。

class Solution:
    directs = [(0,1),(0,-1),(1,0),(-1,0)]
   
    def exist(self, board: List[List[str]], word: str) -> bool:
        m = len(board)
        if m == 0:
            return False
        
        n = len(board[0])
        visited = [[0] * n for _ in range(m)]

        for i in range (0,m):
            for j in range (0,n):
                if self.dfs(i, j, 0, board, word, visited):
                    return True
        return False
    
    def dfs(self, x, y, begin, board, word, visited):
        # 递归出口，如果遍历的index在word的最后，判断盘上是否和单词最后一个是否一样
        if begin == len(word) - 1:
            return board[x][y] == word[begin]

        if board[x][y] == word[begin]:
            # 访问过标记
            visited[x][y] = 1

            for dire in self.directs:
                new_x = x + dire[0]
                new_y = y + dire[1]
                # 遍历四个方向，且保证不越界且没访问过,接着遍历单词的下一个位置
                if 0 <= new_x < len(board) and 0<= new_y < len(board[0]) and visited[new_x][new_y]==0:
                    if self.dfs(new_x, new_y, begin+1, board, word, visited):
                        return True
            # 回溯
            visited[x][y] = 0
        return False

class Solution:
    directs = [(0,1),(0,-1),(1,0),(-1,0)]
   
    def exist(self, board: List[List[str]], word: str) -> bool:
        m = len(board)
        if m == 0:
            return False
        
        n = len(board[0])
        visited = [[0] * n for _ in range(m)]
        def dfs(x, y, begin):
            # 递归出口，如果遍历的index在word的最后，判断盘上是否和单词最后一个是否一样
            if begin == len(word) - 1:
                return board[x][y] == word[begin]
            
    
            if board[x][y] == word[begin]:
                # 访问过标记
                visited[x][y] = 1

                for dire in self.directs:
                    new_x = x + dire[0]
                    new_y = y + dire[1]
                    # 遍历四个方向，且保证不越界且没访问过,接着遍历单词的下一个位置
                    if 0 <= new_x < len(board) and 0<= new_y < len(board[0]) and visited[new_x][new_y]==0:
                        if dfs(new_x, new_y, begin+1):
                            return True
                # 回溯
                visited[x][y] = 0
            return False

        for i in range (0,m):
            for j in range (0,n):
                if dfs(i, j, 0):
                    return True
        return False

208 前缀树

在这里插入图片描述

包含三个单词 “sea”,“sells”,“she” 的 Trie 会长啥样呢？
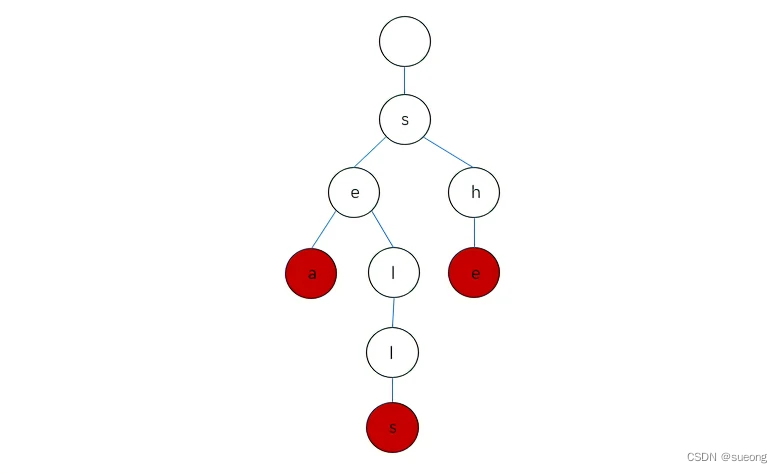
在这里插入图片描述
简化后：
在这里插入图片描述
定义类 Trie

class Trie {
private:
    bool isEnd;
    Trie* next[26];
public:
    //方法将在下文实现...
};

插入
描述：向 Trie 中插入一个单词 word

实现：这个操作和构建链表很像。首先从根结点的子结点开始与 word 第一个字符进行匹配，一直匹配到前缀链上没有对应的字符，这时开始不断开辟新的结点，直到插入完 word 的最后一个字符，同时还要将最后一个结点isEnd = true;，表示它是一个单词的末尾。

void insert(string word) {
    Trie* node = this;
    for (char c : word) {
        if (node->next[c-'a'] == NULL) {
            node->next[c-'a'] = new Trie();
        }
        node = node->next[c-'a'];
    }
    node->isEnd = true;
}

查找
描述：查找 Trie 中是否存在单词 word

实现：从根结点的子结点开始，一直向下匹配即可，如果出现结点值为空就返回 false，如果匹配到了最后一个字符，那我们只需判断 node->isEnd即可。

bool search(string word) {
    Trie* node = this;
    for (char c : word) {
        node = node->next[c - 'a'];
        if (node == NULL) {
            return false;
        }
    }
    return node->isEnd;
}

前缀匹配
描述：判断 Trie 中是或有以 prefix 为前缀的单词

实现：和 search 操作类似，只是不需要判断最后一个字符结点的isEnd，因为既然能匹配到最后一个字符，那后面一定有单词是以它为前缀的。

bool startsWith(string prefix) {
    Trie* node = this;
    for (char c : prefix) {
        node = node->next[c-'a'];
        if (node == NULL) {
            return false;
        }
    }
    return true;
}

链接：https://leetcode.cn/problems/implement-trie-prefix-tree/solution/trie-tree-de-shi-xian-gua-he-chu-xue-zhe-by-huwt/


class Trie:
    # 根节点不存字母
    # next 存了26个字母

    def __init__(self):
        self.next = [None] * 26
        self.isEnd = False


    def insert(self, word: str) -> None:
        node = self
        # 先查找有没有这个字母，没有就新建一个节点，新建后就有该字母的节点，就将树遍历下去
        for ch in word:
            # 如果ch在树中不存在，就新建一个单词的
            if node.next[ord(ch) - ord('a')] == None:
                node.next[ord(ch) - ord('a')] = Trie()
            node = node.next[ord(ch) - ord('a')]
        node.isEnd = True
            


    def search(self, word: str) -> bool:
        node = self
        for ch in word:
             if node.next[ord(ch) - ord('a')] == None:
                 return False
             node = node.next[ord(ch) - ord('a')]
        # 遍历到最后 判断是不是单词的结束
        return node.isEnd


    def startsWith(self, prefix: str) -> bool:
        node = self
        for ch in prefix:
             if node.next[ord(ch) - ord('a')] == None:
                 return False
             node = node.next[ord(ch) - ord('a')]
        # 遍历到最后 不需要判断是不是单词的结束 说明存在prefix 
        return True



# Your Trie object will be instantiated and called as such:
# obj = Trie()
# obj.insert(word)
# param_2 = obj.search(word)
# param_3 = obj.startsWith(prefix)

211. 添加与搜索单词 - 数据结构设计

在这里插入图片描述

思路：和208构建字典树类似
只是查询的时候需要对通配符.特殊处理，
在这里插入图片描述

class WordDictionary:

    def __init__(self):
        self.next = [None] * 26
        self.isEnd = False


    def addWord(self, word: str) -> None:
        node = self
        for ch in word:
            if node.next[ord(ch) - ord("a")] == None:
                node.next[ord(ch) - ord("a")] =  WordDictionary()
            node = node.next[ord(ch) - ord("a")]
        node.isEnd = True


    def search(self, word: str) -> bool:
        root =  self
        def dfs(index,node):
            if index == len(word):
                return node.isEnd
            ch = word[index]
            # 如果ch不是. 看是否存在该字符的节点 如果存在该字符节点 且往后搜索后面的字符 dfs(word下一个字符，树上的下一个节点)
            if ch != '.':
                child = node.next[ord(ch) - ord("a")]
                if child != None and dfs(index+1,child):
                    return True
            # ch 是. ,遍历整个next数组，26个元素，对每个元素都进行dfs
            else:
                for child in node.next:
                    if child != None and dfs(index+1,child):
                        return True
            return False
        return dfs(0,root)
            
            



# Your WordDictionary object will be instantiated and called as such:
# obj = WordDictionary()
# obj.addWord(word)
# param_2 = obj.search(word)

212单词搜索 II

在这里插入图片描述

思路：
对棋盘上的每个位置进行dfs，对输入的单词集合构建成字典树，对于棋盘上的任意位置（i，j）只有在字典树存在从字符a到字符b的边的时候，我们才能在棋盘上找到a-b的路径，

注意：
回溯过程，每次只需要判断新增单元格的字母是否是上一个单元格对应前缀树结点的子结点即可。
在这里插入图片描述

from collections import defaultdict
class TrieNode:
    def __init__(self):
        self.children = defaultdict(TrieNode) 
        #这里要把原来的指针换成map映射 因为要存具体字母的值  如果key不存在也会自动创建再插入不会报错
        self.word = ""# 这里把原来的isEnd换成单词串，如果是结尾存的是单词本身
    
    def insert(self, word):
        node = self
        for ch in word:
            node = node.children[ch] 
        node.word = word

class Solution:
    def findWords(self, board: List[List[str]], words: List[str]) -> List[str]:
        # 给每个单词建立字典树
        trie = TrieNode()
        for word in words:
            trie.insert(word)
        print(trie.children)
        print( "b" in trie.children['o'].children) 
            #         defaultdict(<class '__main__.TrieNode'>, {'o': <__main__.TrieNode object at 0x7f518eeae7d0>, 'p': <__main__.TrieNode object at 0x7f518eef51b0>, 'e': <__main__.TrieNode object at 0x7f518eef52d0>, 'r': <__main__.TrieNode object at 0x7f518eef53f0>})
            # False
      
        m,n = len(board),len(board[0])
        directions = [(0,1),(0,-1),(1,0),(-1,0)]

    
        def dfs(x, y, node):
            # 加上也没错 但是运行时间会变长，因为多判断了一次 进入dfs永远不会经过这个 因为最后回溯都会复原 进入的xy也在范维内
            # if  not( 0<= x < m and 0 <= y < n) or board[x][y]=="#":
            #     return
            # 如果当前位置字符不在字典树当前节点的孩子中，直接返回
            ch = board[x][y]
            if ch not in node.children:
                return
            
            # 获取当前字符对应的子节点 
            child = node.children[ch]

            # 说明是单词结尾，加入结果集
            if child.word!="":
                res.add(child.word)
            
            # 如果不是单词结尾，标记已访问，探索该点的四个方向,说明应该有孩子节点
            if child.children: #!!关键语句 可以使运行时间减半
                board[x][y] = '#'
                for dire in directions:
                    new_x = x + dire[0]
                    new_y = y + dire[1]
                    # 边界符合且未访问过 dfs(board的新位置，字典树的下一个节点即孩子节)
                    if 0<= new_x < m and 0 <= new_y < n and board[new_x][new_y]!="#":
                        dfs(new_x, new_y, child)
                # 回溯
                board[x][y] = ch




        
        #存储搜索到的单词
        res  = set()
        # 对棋盘上的每个位置都dfs
        for i in range(m):
            for j in range(n):
                dfs(i,j,trie)
        return list(res)

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/487348.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Mysql 主从 读写分离

Mysql 主从 读写分离

目录 0 课程视频 1 概述 1.1原理 -> 传二进制日志到 从库 -> 执行 1.2 作用 1.2.1 主库崩 从库上 1.2.2 读写分离 1.2.3 从库备份 -> 备份完 再用 二进制日志同步 2 搭建 2.1 防火墙 端口号开启 2.2 主库设置 2.2.1 修改配置文件 -.> /etc/my.cnf 2.2…
阅读更多...
高压放大器模块在平面水声压电换能器研究中的应用

高压放大器模块在平面水声压电换能器研究中的应用

实验名称&#xff1a;平面水声压电换能器的制备与性能研究 研究方向&#xff1a;压电换能器 实验原理&#xff1a; 压电换能器是能够发射和接收超声波的电声转换器件&#xff0c;按照不同的标准&#xff0c;换能器可分为不同的种类。按照功能可分为发射型、接收型和收发两用…
阅读更多...
亚马逊下单需要什么条件？（养号干货知识）

亚马逊下单需要什么条件？（养号干货知识）

混迹亚马逊的老手都知道&#xff0c;测评向来都是最有效&#xff0c;最快速的推广方式&#xff0c;给自己商品做点销量&#xff0c;优化一下listing&#xff0c;留一下一些优质评论&#xff0c;甚至于打压一下竞品&#xff0c;帮自己商品解个围。 养号环境四大步&#xff1a; …
阅读更多...
定制海报、AI扣人像小程序

定制海报、AI扣人像小程序

大家好，我是csdn的博主：lqj_本人 这是我的个人博客主页： lqj_本人的博客_CSDN博客-微信小程序,前端,python领域博主lqj_本人擅长微信小程序,前端,python,等方面的知识https://blog.csdn.net/lbcyllqj?spm=1011.2415.3001.5343哔哩哔哩欢迎关注：小淼Develop 小淼Develop的个…
阅读更多...
nakamichi车机中控屏密码破解(开发者选项密码、usb主从模式切换密码)

nakamichi车机中控屏密码破解(开发者选项密码、usb主从模式切换密码)

版本 Android11 平台 mtk 打开开发者选项&#xff0c;连续点击系统版本号会弹出密码框确认 这个默认密码这台设备并没有配置&#xff0c;而是动态的 默认密码 SystemProperties.get(“ro.sys.developer”, “”); 动态根据设备当前日前来生成的格式为 yyyy.MM.dd 所以上面的…
阅读更多...
Node框架 【Koa】开发框架、路由

Node框架 【Koa】开发框架、路由

文章目录 &#x1f31f;前言&#x1f31f;开发框架&#x1f31f;应用程序&#x1f31f;应用程序Koa类&#x1f31f;应用对象(app)的方法&#x1f31f;app.use(function)&#x1f31f;app.listen(...) &#x1f31f;应用程序设置 &#x1f31f;上下文(Context) &#x1f31f;路由…
阅读更多...
电脑c盘满了变成红色了怎么清理？看看这7个方法

电脑c盘满了变成红色了怎么清理？看看这7个方法

当C盘出现红色标识提示时&#xff0c;表示该分区的可用存储空间已经极度不足&#xff0c;可能会影响系统稳定性和性能。如果您需要清理C盘并腾出更多的存储空间&#xff0c;可以采取以下措施&#xff1a; 一、电脑c盘7种清理方法 方法1&#xff1a;清空回收站 演示机型&#…
阅读更多...
pytorch优化器——add_param_group()介绍及示例、Yolov7 优化器代码示例

pytorch优化器——add_param_group()介绍及示例、Yolov7 优化器代码示例

系列文章目录 基础函数2——enumerate()、hasattr()、isinstance() pytorch学习率设置——optimizer.param_groups、对不同层设置学习率、动态调整学习率。 文章目录 系列文章目录前言1、关于pytorch优化器2、add_param_group()3、pytorch优化器4、pytorch优化器测试总代码5、…
阅读更多...
如何保证 RabbitMQ 的消息可靠性

如何保证 RabbitMQ 的消息可靠性

前言 项目开发中经常会使用消息队列来完成异步处理、应用解耦、流量控制等功能。虽然消息队列的出现解决了一些场景下的问题&#xff0c;但是同时也引出了一些问题&#xff0c;其中使用消息队列时如何保证消息的可靠性就是一个常见的问题。如果在项目中遇到需要保证消息一定被…
阅读更多...
大数据技术之Hadoop-入门

大数据技术之Hadoop-入门

第1章 Hadoop概述 1.1 Hadoop是什么 分布式&#xff1a;多台服务器共同完成某一项任务。 1.2 Hadoop发展历史 1.3 Hadoop三大发行版本 Hadoop三大发行版本&#xff1a;Apache、Cloudera、Hortonworks。 Apache版本最原始&#xff08;最基础&#xff09;的版本&#xff0c…
阅读更多...
【三十天精通Vue 3】第二十六天 Vue3 与 TypeScript 最佳实践

【三十天精通Vue 3】第二十六天 Vue3 与 TypeScript 最佳实践

✅创作者&#xff1a;陈书予 &#x1f389;个人主页&#xff1a;陈书予的个人主页 &#x1f341;陈书予的个人社区&#xff0c;欢迎你的加入: 陈书予的社区 &#x1f31f;专栏地址: 三十天精通 Vue 3 文章目录 引言一、为什么使用TypeScript&#xff1f;二、Vue 3和TypeScript…
阅读更多...
Golang每日一练(leetDay0055)

Golang每日一练(leetDay0055)

目录 159.至多包含两个不同字符的最长子串 Longest-substring-with-at-most-two-distinct-characters &#x1f31f;&#x1f31f; 160. 相交链表 Intersection-of-two-linked-lists &#x1f31f; &#x1f31f; 每日一练刷题专栏 &#x1f31f; Golang每日一练 专栏 …
阅读更多...
Stable Diffusion +ChatGPT+文本转语音+剪映制作视频

Stable Diffusion +ChatGPT+文本转语音+剪映制作视频

目录 chatgpt免费体验入口网址 模型下载 huggingface.co civitai.com 使用Deliberate模型案例 StableDeffusion做的图片&#xff0c;chatGPT出的文案&#xff0c;微软文本转语音配的音&#xff0c;使用剪映做的视频 chatgpt免费体验入口网址 http://chat.xutongbao.top …
阅读更多...
【Java数据结构】顺序表、队列、栈、链表、哈希表

【Java数据结构】顺序表、队列、栈、链表、哈希表

顺序表 定义 存放数据使用数组但是可以编写一些额外的操作来强化为线性表&#xff0c;底层依然采用顺序存储实现的线性表&#xff0c;称为顺序表 代码实现 创建类型 先定义一个新的类型 public class ArrayList<E> {int capacity 10; //顺序表的最大容量int size …
阅读更多...
UNIX环境高级编程——信号

UNIX环境高级编程——信号

10.1 引言 信号是软件中断&#xff1b;信号提供了一种处理异步事件的方法。 10.2 信号概念 每个信号都有一个名字&#xff0c;这些名字都以3个字符SIG开头&#xff1b;在头文件<signal.h>中&#xff0c;信号名都被定义为正整数常量&#xff08;信号编号&#xff09;&a…
阅读更多...
架构设计-高性能篇

架构设计-高性能篇

大家好&#xff0c;我是易安&#xff01;今天我们谈一谈架构设计中的高性能架构涉及到的底层思想。本文分为缓存架构&#xff0c;单服务器高性能模型&#xff0c;集群下的高性能模型三个部分&#xff0c;内容很干&#xff0c;希望你仔细阅读。 高性能缓存架构 在某些复杂的业务…
阅读更多...
代码审计笔记之java多环境变量设置

代码审计笔记之java多环境变量设置

在做java代码审计时&#xff0c;为了要成功运行目标环境&#xff0c;时长要对于jdk版进行切换&#xff0c;且在装多个jdk时还时长会遇到安装配置后环境变量不生效的情况&#xff0c;下文介绍&#xff1b; 1、为什么安装了新的jdk&#xff0c;有的时候环境变量中的jdk版本确还是…
阅读更多...
如何设计出好的测试用例?

如何设计出好的测试用例?

软件测试培训之如何设计出好的测试用例? 一句话概括&#xff1a;对被测软件的需求有深入的理解。 深入理解被测软件需求的最好方法是&#xff0c;测试工程师在需求分析和设计阶段就开始介入&#xff0c;因为这个阶段是理解和掌握软件的原始业务需求的最好时机。 只有真正理解了…
阅读更多...
【VAR模型 | 时间序列】帮助文档：VAR模型的引入和Python实践（含源代码）

【VAR模型 | 时间序列】帮助文档：VAR模型的引入和Python实践（含源代码）

向量自回归 (VAR) 是一种随机过程模型&#xff0c;用于捕获多个时间序列之间的线性相互依赖性。 VAR 模型通过允许多个进化变量来概括单变量自回归模型&#xff08;AR 模型&#xff09;。 VAR 中的所有变量都以相同的方式进入模型&#xff1a;每个变量都有一个方程式&#xff…
阅读更多...
轻松掌握在已有K8s环境上安装KubeSphere

轻松掌握在已有K8s环境上安装KubeSphere

官方文档地址&#xff1a;https://kubesphere.io/zh/docs/v3.3/quick-start/minimal-kubesphere-on-k8s/ 1、基于已有K8s环境上安装KubeSphere 1、前置环境 1、安装nfs及动态存储类PV/PVC 安装默认存储类型&#xff0c;这里使用nfs&#xff0c;关于nfs的安装在PV/PVC的文章…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023