顺序表

定义

存放数据使用数组但是可以编写一些额外的操作来强化为线性表，底层依然采用顺序存储实现的线性表，称为顺序表

代码实现

创建类型

先定义一个新的类型

public class ArrayList<E> {
    int capacity = 10; //顺序表的最大容量
    int size = 0; //当前已经存放的元素数量
    private Object[] array = new Object[capacity]; //底层存放的数组
}

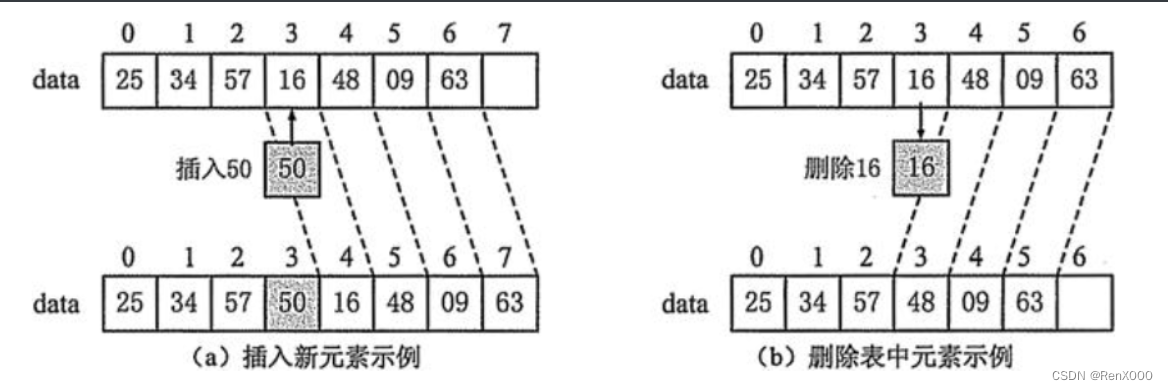
由此可见，顺序表是紧凑的，不能出现空位

插入

但是这样少了条件限制，也就是容量的问题，范围只是[0,size]，所以需要判断

public void add(E element, int index) {
    if(index<0 || index>size)
        throw new IndexOutOfBoundsException("invalid, size:0~"+size);
    for(int i=size; i>index; i--) {
        array[i] = array[i-1];
    }
    array[index] = element;
    size++;
}

public static void main(String[] args) {
    ArrayList<Integer> list = new ArrayList<>();
    list.add(10,1); //是一个可以得到异常的函数
}

此时此刻，就很成功的报错了

完善 - 扩容

我们可以让我们的操作更加完美，比如，扩容

public void add(E element, int index) {
    if(index<0 || index>size)
        throw new IndexOutOfBoundsException("invalid, size:0~"+size);
    if(capacity == size) {
        int newCapacity = capacity +(capacity >> 1);
        Object[] newArray = new Object[newCapacity];
        System.arraycopy(array, 0, newArray, 0, size);
        array = newArray;
        capacity = newCapacity;
    }
    for(int i=size; i>index; i--) {
        array[i] = array[i-1];
    }
    array[index] = element;
    size++;
}

打印

public String toString() {
    StringBulider bulider = new StringBuilder();
    for(int i=0; i<size; i++) {
        builder.append(array[i].append(" "));
        return builder.toString();
    }
}

删除

@SuppressWarnings("unchecked")
public E remove(int index){
    if(index < 0 || index > size - 1)
        throw new IndexOutOfBoundsException("删除位置非法，合法的插入位置为：0 ~ "+(size - 1));
    E e = (E) array[index];
    for (int i = index; i < size; i++)
        array[i] = array[i + 1];
    size--;
    return e;
}

获取

public E get(int index) {
if(index<0 || index>(size-1)) 
	throw new IndexOutOfBoundsException("invalid: position 0~" +(size-1));
return (E) array[index];
}

public int size() {
	return size;
}

链表

链表通过指针来连接各个分散的结点，形成链状的结构，不需要申请连续的空间，逻辑依然是每个元素相连

链表分带头结点的和不带头结点的

带头结点的就是不存放数据，一般设计都会采用带头结点的

设置

public class LinkedList<E> {
    private final Node<E> head = new Node<>(null);
	private int size = 0;

	private static class Node<E> {
   		E element;
    	Node<E> next;
    	public Node(E element) {
        	this.element = element;
    	}
	}
}

插入

考虑的点：插入位置是否合法

public void add(E element, int index){
    if(index < 0 || index > size)
        throw new IndexOutOfBoundsException("插入位置非法，合法的插入位置为：0 ~ "+size);
    Node<E> prev = head;
    for (int i = 0; i < index; i++)
        prev = prev.next;
    Node<E> node = new Node<>(element);
    node.next = prev.next;
    prev.next = node;
    size++;
}

重写 toString()

@Override
public String toString() {
	StringBuilder builder = new StringBuilder();
    Node<E> node = head.next;
    while(node != null) {
        bulider.append(node.element).append(" ");
        node = node.next;
    }
    return builder.toString();
}

删除

public E remove(int index) {
    if(index<0 || index>size-1) {
        throw new IndexOutOfBoundsException("invalid,position: 0~" + (size - 1));
    }
    Node<E> prev = head;
    for(int i=0; i<index; i++) {
        prev = prev.next;
    }
    E e = prev.next.element;
    size--;
    return e;
}

获取对应位置上的元素

public E get(int index) {
    if(index<0 || index>size-1) {
        throw new IndexOutOfBoundsException("invalid position:0~" + (size-1));
    }
    Node<E> node = head;
    while(index-- >= 0) {
        node = node.next;
    }
    return node.element;
}

public int size() {
    return size;
}

总结

链表在随机访问数据的时候，需要通过遍历来完成，而顺序表则利用数组的特性可以直接访问得到，当我们读取数据多于插入删除操作的时候，使用顺序表会更好；顺序表在进行插入删除操作的时候，因为需要移动后续元素，会很浪费时间，链表则不需要，只需要修改结点的指向就行了。所以在进行频繁的插入删除操作的时候，使用链表必然是更好的

栈-先进后出

**FILO: First in, Last out **

是一种特殊的线性表，只能在表尾进行插入删除操作；有点像堆积木，最后堆上去的往往是最先拿下来的

底部称为栈底，顶部称为栈顶；所有的操作只能在栈顶进行

栈可以使用顺序表实现，也可以使用链表实现，使用链表会更加方便。直接将头结点指向栈顶结点，而栈顶结点连接后续的栈内结点

链表实现

类

public class LinkedStack<E> {
    private final Node<E> head = new Node<>(null);
    private static class Node<E> {
        E element;
        Node<E> next;
        public Node(E element) {
            this.element = element;
        }
    }
}

入栈操作

public pop() {
    if(head.next == null) {
        throw new NoSuchElementException("Stack is empty");
    }
    E e = head.next.element;
    return e;
}

测试

public static void main(String[] args) {
    LinkedStack<String> stack = new LinkedStack<>();
    stack.push("AAA");
    stack.push("BBB");
    stack.push("CCC");
    System.out.println(stack.pop());
    System.out.println(stack.pop());
    System.out.println(stack.pop());
}

队列

FIFO First in First out

类似于在超市买东西，先进先出
队列有队头和队首
实现方式：链表、顺序表
利用链表则不需要考虑容量的问题，我们需要同时保存队首和队尾两个指针

创建队列

public class LinkedQueue<E> {
	private final Node <E> head = new Node<>(null);
//入队操作
	public void offer(E element) {
		Node<E> last = head;
		while(last.next != null) {
			last = last.next;
		}
		last.next = new Node<>(element);
	}
//出队操作
	public E pull() {
		if(head.next == null) 
			throw new NoSuchElementException(“Queue is empty”);
		E e = head.next.element;
		head.next = head.next.next;
		return e;
	}

	private static class Node<E> {
		E element;
		Node<E> next;
		public Node(E element) {
			this.element = element;
		}
}

使用

public static void main(String[] Args) {
	LinkedQueue<String> stack = new LinkedQueue<>();
	stack.offer(“AAA”);
	stack.offer(“BBB”);
	stack.offer(“CCC”);
	System.out.println(stack.pull());
	System.out.println(stack.pull());
	System.out.println(stack.pull());

哈希表

散列（Hashing)通过散列函数（哈希函数）将要参与检索的数据与散列值（哈希值）关联，生成一种便于搜索的数据结构，称其为散列表（哈希表）

我们需要将一堆数据保存起来，这些数据会通过哈希函数进行计算，得到与其对应的哈希值，下次需要查找的时候，只需要再次计算哈希值就行了

哈希函数在现实生活中应用十分广泛，目前应用最广泛的是SHA-1、MD5；比如我们下载的IDEA，她的校验文件，就是安装包文件通过哈希算法计算得到的

我们可以将这些元素保存到哈希表，保存的位置与其对应的哈希值有关，哈希值是通过哈希函数计算得到的，我们只需要将对应元素的key提供给哈希函数就可以进行计算了。一般比较简单的哈希函数就是取模操作。哈希表长度（最好是素数）多少，模就是多少

保存到数据是无序的，我们并不清楚计算完哈希值之后会被放到那个位置，哈希表在查找时只需要进行一次哈希函数计算就能直接找到对应元素的存储位置，效率极高

实现简单的哈希表和哈希函数，通过哈希表，可以将数据的查找时间复杂度提升到常数阶

public class HashTable<E> {
    private final int TABLE_SIZE = 10;
    private final Object[] TABLE = new Object[TABLE_SIZE];
    
    public void insert(E element) {
        int index = hash(element);
        TABLE[index] = element;
    }
    
    public boolean contains(E element) {
        int index = hash(element);
        return TABLE[index] == element;
    }
    
    private int hash(Object object) {
        int hashCode = object.hashCode(); //每一个对象都有一个独一无二的哈希值，可以通过hashCode方法得到，只有极小概率会重复
        return hashCode % TABLE_SIZE;
    }
}

会出现哈希碰撞的情况，也就是不同的元素计算出来的哈希值是一样的，这种情况是不可避免的，我们只能通过使用更加高级的哈希函数来尽可能避免这种情况

常见的哈希冲突解决方案是链地址法 ，当出现哈希冲突的时候，我们依然将其保存在对应的位置上，可以将其连接为一个链表的形式

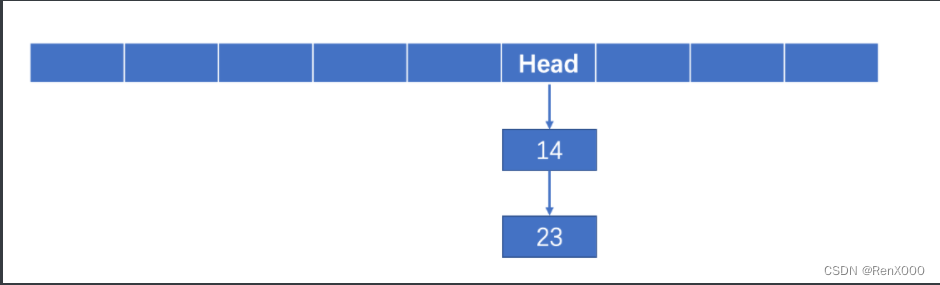
当元素太多的时候，我们一般将其横过来看

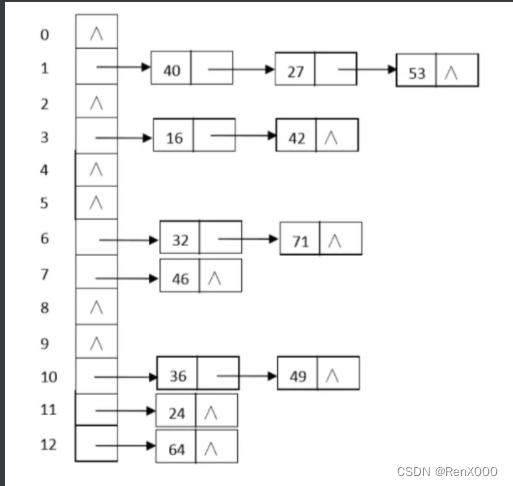
但是当链表变得很长的时候，查找效率也就会变得很低下，所以我们可以考虑在链表长度达到一定值的时候，使用其他数据结构，例如平衡二叉树、红黑树，这样就可以一定程度上缓解查找的压力

public class HashTable<E> {
    private final int TABLE_SIZE = 10;
    private final Node<E>[] TABLE = new Node[TABLE_SIZE];
    
    public HashTable() {
        for(int i=0; i<TABLE_SIZE; i++) {
            TABLE[i] = new Node<>(null);
        }
    }
    
    public void insert(E element) {
        int index = hash(element);
        Node<E> prev = TABLE[index];
        while(prev.next != null) {
            prev = prev.next;
        }
        prev.next = new Node<>(element);
    }
    
    public boolean contains(E element) {
        int index = hash(element);
        Node<E> node = TABLE[index].next;
        while(node != null) {
            if(node.element == element) 
                return true;
            node = node.next;
        }
        return false;
    }
    
    private int hash(Object object) {
        int hashCode = object.hashCode();
        return hashCode % TABLE_SIZE;
    }
    
    private static class Node<E> {
        private final E element;
        private Node<E> next;
        
        private Node(E element) {
            this.element = element;
        }
    }
}