浮点数渐进下溢

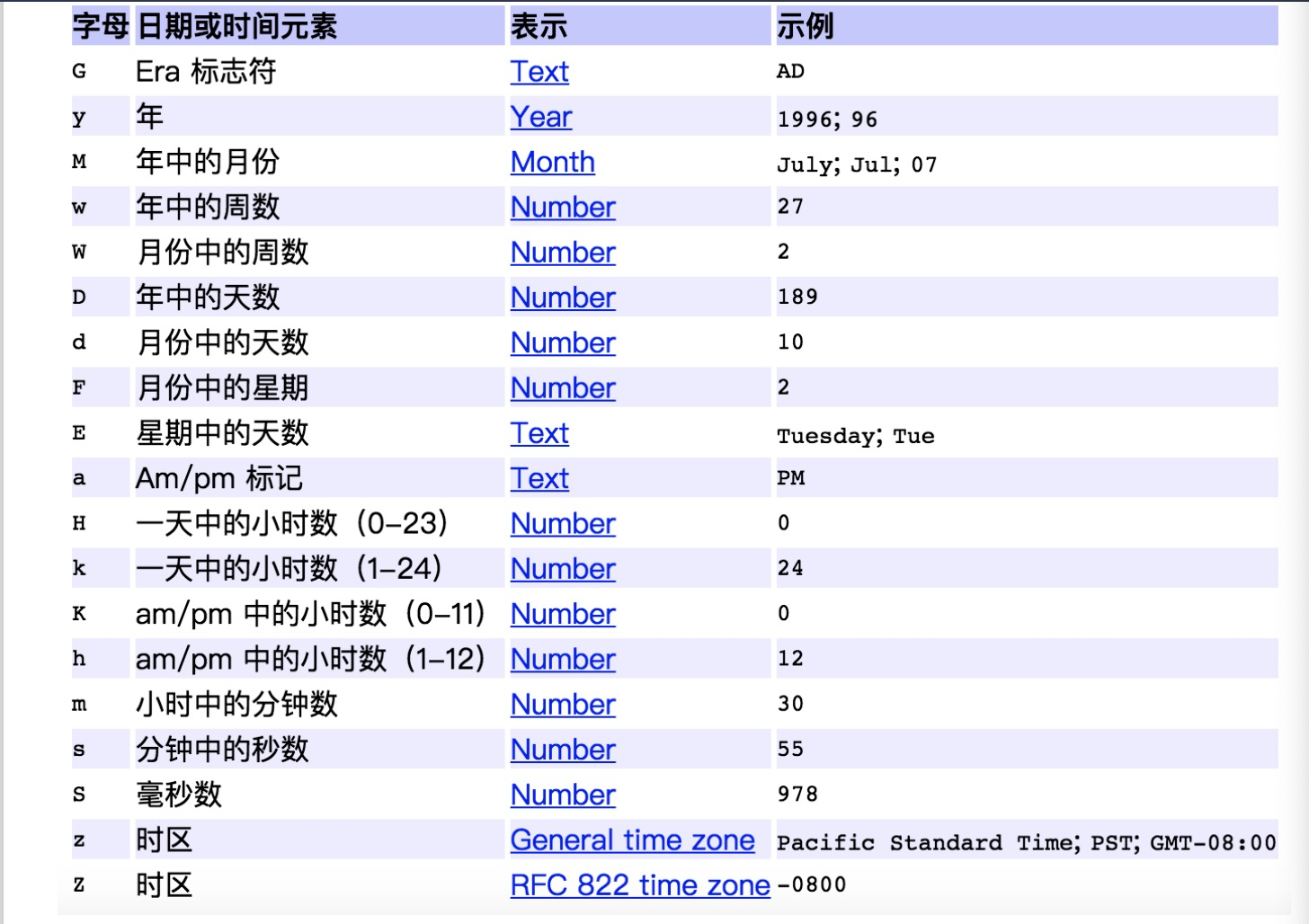
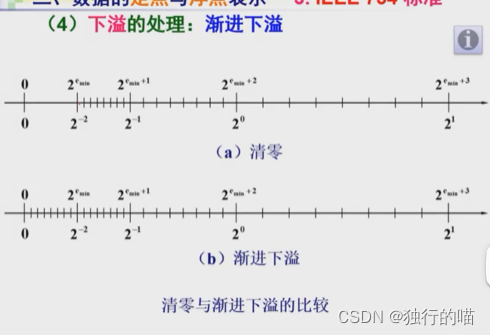
当IEEE754浮点数的运算结果或转化结果中，存在阶码全0的情况时，在IEEE754标准的描述中说，若此时尾数不全为0，则表示次正规数，即次数浮点数的真值其实应该成为：
$$(-1{)}^s\ast 0.f\ast 2^{e_{min}}$$

案列及规则描述如下：

例题：Y=0.375 Z为IEEE754单精度浮点数，Z的十六进制内容为FE000000，问：Y/Z的结果是否溢出，如果溢出，除法运算后应如何返回Y/Z的结果。

分析：Y的IEEE754规格化二进制数为：$1.100\ast 2^{-2}$
Z的IEEE754规格化二进制数为：$-1.000\ast 2^{125}$
采用浮点数除法运算的规则，其结果为$-1.100\ast 2^{-127}$
此时阶码取到了IEEE754单精度浮点数规定的阶码最小值-1，即就是阶码全0的特殊情况，并且尾数不为0，所以应该采取渐进下溢的方法用次正规数来返回结果：

• 尾数右规一位，阶码+1后：$-0.1100\ast 2^{-126}$
• 将$-0.1100\ast 2^{-126}$作为Y/Z的运算结果返回