1、等价关系（Equivalence Relations）

等价关系

定义1： 定义在集合 A 上的关系叫做等价关系，如果它们是 自反的、对称的和传递的。

等价的元素

定义2： 如果两个元素 a 和 b 由于等价关系而相关联，则称它们是等价的。记法 a~b 通常用来表示对于某个特定的等价关系来说，a 和 b 是等价的元素。

📘例1：模m同余

设 m 是大于 1 的整数。证明以下关系是定义在整数集上的等价关系：
R = { (a, b) | a ≡ b (mod m) }

解：
根据模m同余定义， a ≡ b (mod m) 当且仅当 m 整除 a – b
要证明等价关系 ➩ 证明自反性、对称性、传递性：

自反性： a ≡ a (mod m)，因为 a − a = 0 被 m 整除，因为 0 = 0 ∙ m。

对称性： 假设a ≡ b (mod m)，那么 a – b 可以被 m 整除，所以 a – b = km， 其中 k 是整数。因此，b – a = (– k)m，所以 b ≡ a (mod m)

传递性： 假设 a ≡ b (mod m) 和 b ≡ c (mod m)，那么 m 同时整除 a – b和 b – c，因此存在整数有 k 和 l，使得 a – b = km 和 b – c = lm，将方程相加有：a − c = (a − b) + (b − c) = km + lm = (k + l)m。因此，a ≡ c (mod m)
综上，自反性、对称性、传递性均满足，因此R = { (a, b) | a ≡ b (mod m) }是定义在整数集上的等价关系

📘例2：字符串

设 R 是定义在英文字母组成的字符串的集合上的关系，满足 aRb 当且仅当 l(a) = l(b)，其中 l(x) 是字符串 x 的长度。R 是等价关系吗？

解：证明等价关系的所有性质都成立。

自反性： 因为 l(a) = l(a)，只要 a 是一个字符串，就有 aRa。
对称性： 假设 aRb，即 l(a) = l(b)，那么有 bRa 因为 l(b) = l(a) 。
传递性： 假设 aRb 且 bRs 则有 l(a) = l(b) 和 l(b)= l(s)，因此 l(a) = l(s)，即 aRc。
综上，R是等价关系

📘例3：整除

证明定义在正整数集合上的“整除”关系不是等价关系。

解：

自反性： 对所有 a，a ∣ a。
对称性： 例如，2 ∣ 4，但 4 ∤ 2。不满足对称性
传递性： 假设 a 整除 b，b 整除 c。有正整数 k 和 l，使得 b = ak，c = bl，因此 c = a(kl)，所以 a 整除 c 。

“整除”关系是自反和传递的，但是此关系不是对称的。因此正整数上的“整除”关系不是等价关系

2、等价类（Equivalence Classes）

等价类

定义： 设 R 是定义在集合 A 上的等价关系。与 A 中的一个元素 a 有关系的所有元素的集合叫做 a 的等价类。A 的关于 R 的等价类记作 [a]_R。当只考虑一个关系时，我们将省去下标 R 并把这个等价类写作 [a]

换句话说，如果R是定义在A上的等价关系，则元素a的等价类：[a]_R = { s | (a, s)∈R }
❗ 注意：等价类 [a]_R 非空

代表元

如果 b∈[a]_R，b 叫做这个等价类的代表元。
一个等价类的任何元素都可以作为这个类的代表元。
也就是说，选择特定元素作为一个类的代表元没有特殊要求

// 模 m 同余关系的等价类叫做模 m 同余类。整数 a 模 m 的同余类记作 [a]_m

3、等价类与划分

等价类性质

定理1： 设 R 是定义在集合 A 上的等价关系，下面的关于集合 A 中 a、b 两个元素的命题是等价的：
(i) aRb
(ii) [a] = [b]
(iii) [a] ∩ [b] ≠ ∅

❗

1、不相等的等价类必然不相交
2、有公共元素的任意两个等价类必相等

➩ 等价类或者是相等的或者是不相交的

划分

定义： 集合 S 的划分是 S 的不相交的非空子集构成的集合，且它们的并集就是 S。

//是划分一定是覆盖（后面讲覆盖）

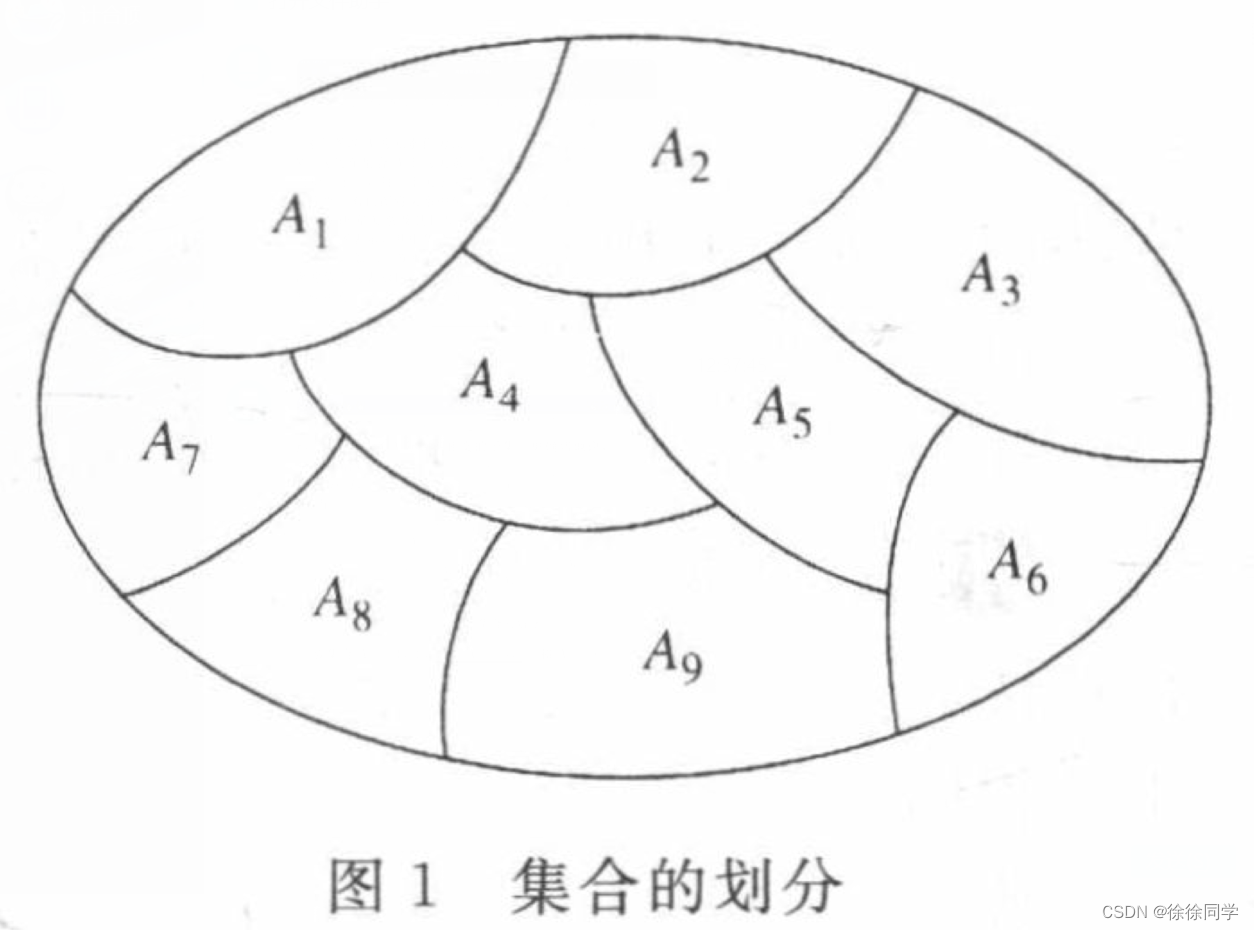
等价关系划分集合

设 R 是定义在集合 A 上的等价关系，R 的所有等价类的并集就是集合 A，因为 A 的每个元素 a 都在它自己的等价类。

定理2：设 R 是定义在集合 S 上的等价关系。那么 R 的等价类构成 S 的划分。反过来，给定集合 S 的划分 { A_i | i ∈ I }，则存在一个等价关系 R，它以集合 A_i (i ∈ I) 作为它的等价类

🔺给定集合的划分，求该划分产生的等价关系的有序对

方法： 把所给划分的每一个集合自乘 ,再取并（∪）

📘例：

列出由 {a, b, c, d, e} 的划分 {a, b}, {c}, {d, e} 产生的等价关系的有序对：
R1 = {a, b} × {a, b} = {（a , a), (a , b), (b, a), (b, b)}
R2 = {c} × {c} = { (c, c) }
R3 = {d, e} × {d, e} = {(d, d), (d, e), (e, d), (e, e)}
R = R1 ∪ R2 ∪ R3 = {(a, a), (a, b), (b, a), (b, b), (c, c), (d, d), (d, e),(e, d), (e, e)}

4、等价类与商集

设 R 是定义在集合 A 上的等价关系，R 的所有等价类的集合{ [a]_R | a∈A }称作A关于R的商集，记做A/R

结论1： 定义在集合 A 上的等价关系R, 决定了A的一个划分，该划分就是商集A/R。
结论2： 集合A 的一个划分确定A的元素间的一个等价关系

A=A₁∪A₂∪…∪A_n (A_i ∩ A_j= ∅,i ≠ 𝑗 ), 则R=A₁ × A₁∪A₂ × A₂∪…∪A_n × A_n

* 由n个元素组成的有限集合A上所有的等价关系的个数

由n个元素组成的有限集合上所有的等价关系的个数为多少？
= 2ⁿ -1

为什么？？？

因为集合A上的等价关系与A的划分是一 一对应的，所以n个元素的有限集上等价关系的数目，与n个元系集合进行划分的数目是相同的，C_n¹+C_n²+…+C_nⁿ = 2ⁿ -1