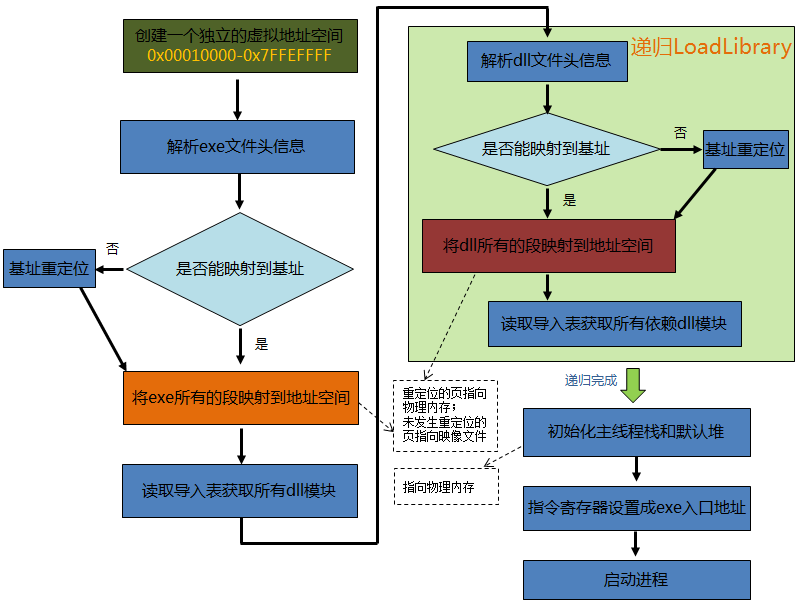
在语音处理进行短时傅里叶变换的时候，对窗函数是有一定要求的，这篇文章将对这方面的问题进行简单的阐述。

一、背景描述

       常用的语音处理需要进行这样处理:

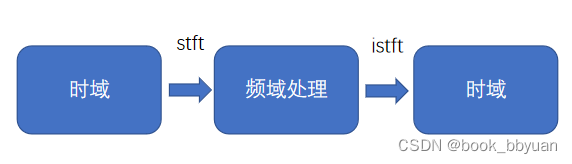
stft分帧会对信号产生截断，为尽可能避免这种影响，应考虑考虑加合适的窗

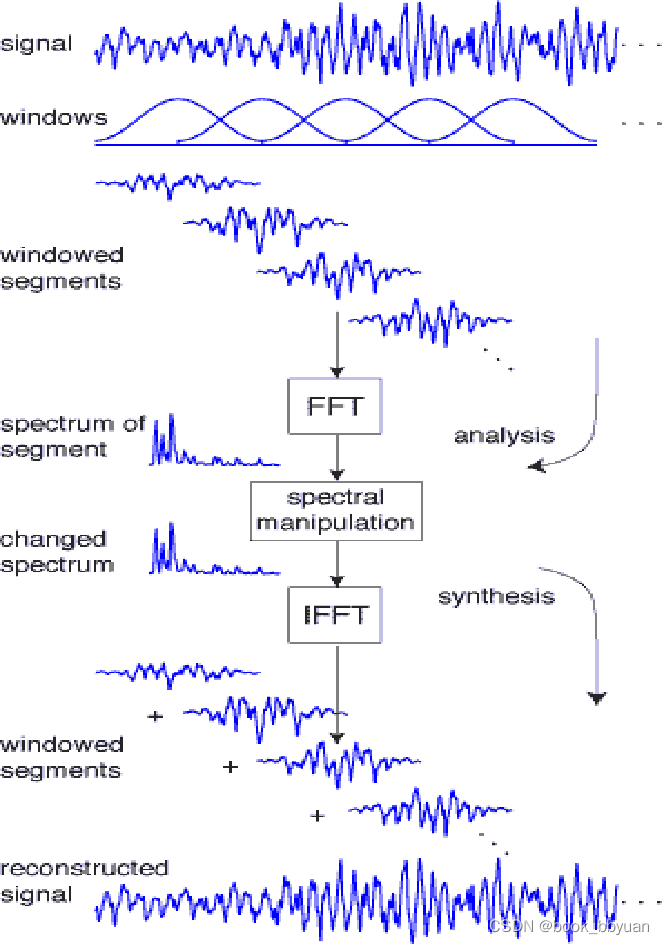
这种方法叫 overlap and add ，或者 OLA 

由上图可以看到，信号需要经过两次加窗（分析窗和合成窗，一般用一样的），另外加窗处理之后还要能重建，则需要对窗函数有特殊要求，这种要求叫 COLA compliance ，全称 Constant Overlap-Add (COLA) Constraint

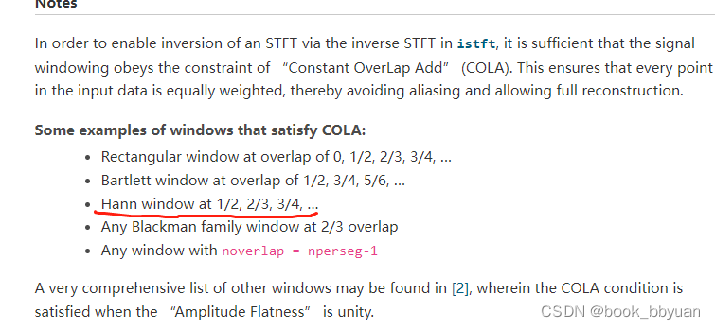
一些特殊的窗，加上特殊的hopsize（or overlap），才可能达到。也从上面可以给出结论：

至少要保证1/2及以上的重叠才能达到完美重建目的

二、Matlab中的例子

matlab里面专门有个函数 iscola，用来判断所设计的窗是否满足条件。举一个例子，窗长是120，每次hop 是一半：

window = sqrt(hann(120,'periodic')); %开方式因为每次操作会经过两遍一样的窗
noverlap = 60; 
[tf,m,maxDeviation] = iscola(window,noverlap)

我们通过作图来看看是否符合要求

 这里可以做一个简单的推导证明：hann窗如下

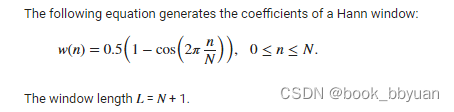
 注意到原始分析窗（or合成窗）是开方了的，所以经过两遍加窗，信号实际乘的窗还是回到w(n）

在0到N/2 这段（其它段以次类推），两部分窗由于叠加，他们的和是

0.5(1-cos(2*pi*n/N) (上图蓝色部分） +  0.5(1-cos(2*pi*(n+N/2)/N) （上图红色部分平移到0-N/2）

= 0.5-0.5*cos(2*pi*n/N) + 0.5 - 0.5*cos(2*pi*n/N+pi) 

=1-0.5*cos(2*pi*n/N)+ 0.5*cos(2*pi*n/N)[这边对上80后的统一暗号，纵变横不变，符号看象限！]

=1

对于1/2 overlap（用的最多）

在分析窗时，填充新数据在尾部，再乘以窗函数，合成时候，踢出前半段和保留数据做和，尾部橙色部分保留等下次再输出

三、一般长度的窗设计

如果我只有160个点输入，但是想用256点的加速FFT运算，那么需要怎么设计这个窗呢？

（当然也可以考虑补零到256，但是ifft回来之后怎么得到160个点？）

这种情况下，overlap = 256-160=96，可以设计 2*overlap的窗，对半劈开拉远，然后中间补1

具体代码如下：

nwin = 2*overlap; fftsize =256;

win = sqrt(hann(nwin,'periodic'));
nwin = length(win);
win1 = [win(1:0.5*nwin);ones(fftsize-noverlap*2,1);win(0.5*nwin+1:end)];
plot(win1);

tf = iscola(win1,noverlap);

 设计一个256长的buffer，每次从尾部更新160个数据，要保留96个数据为下次使用

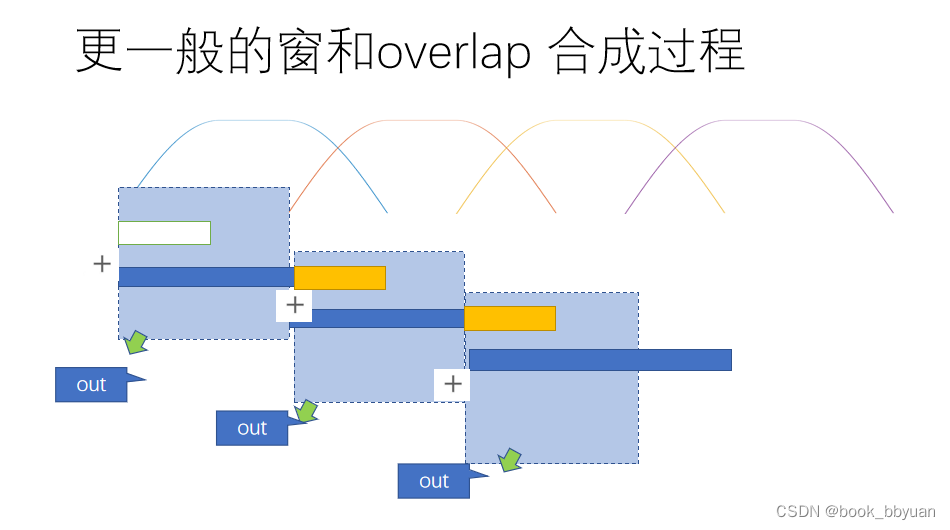
 合成窗需要一个96的outbuffer用来做预输出，每次和加完窗之后的数据做和