翻译：

序列的权值定义为具有相同值(𝑎𝑖=𝑎𝑗)的无序索引对(𝑖，𝑗)(这里𝑖<𝑗)的数量。例如，序列𝑎=[1,1,2,2,1]的权值为4。具有相同值的无序索引对的集合是(1,2)，(1,5)，(2,5)和(3,4)。

给您一个𝑛整数的序列𝑎。打印𝑎的所有子段的权重之和。

序列𝑏是序列𝑎的子段，如果可以通过删除开始部分的几个(可能是零或全部)元素和结束部分的几个(可能是零或全部)元素从𝑎获得𝑏。

输入
每个测试包含多个测试用例。第一行包含测试用例的数量𝑡(1≤𝑡≤105)。测试用例的描述如下。

每个测试用例的第一行包含一个整数𝑛(1≤𝑛≤105)。

每个测试用例的第二行包含𝑛整数𝑎1，𝑎2，…，𝑎𝑛(1≤𝑎𝑖≤109)。

可以保证所有测试用例中𝑛的总和不超过105。

输出
对于每个测试用例，打印一个整数—𝑎的所有子段的权值之和。

例子
inputCopy
2
4
1 2 1 1
4
1 2 3 4
outputCopy
6
0
请注意
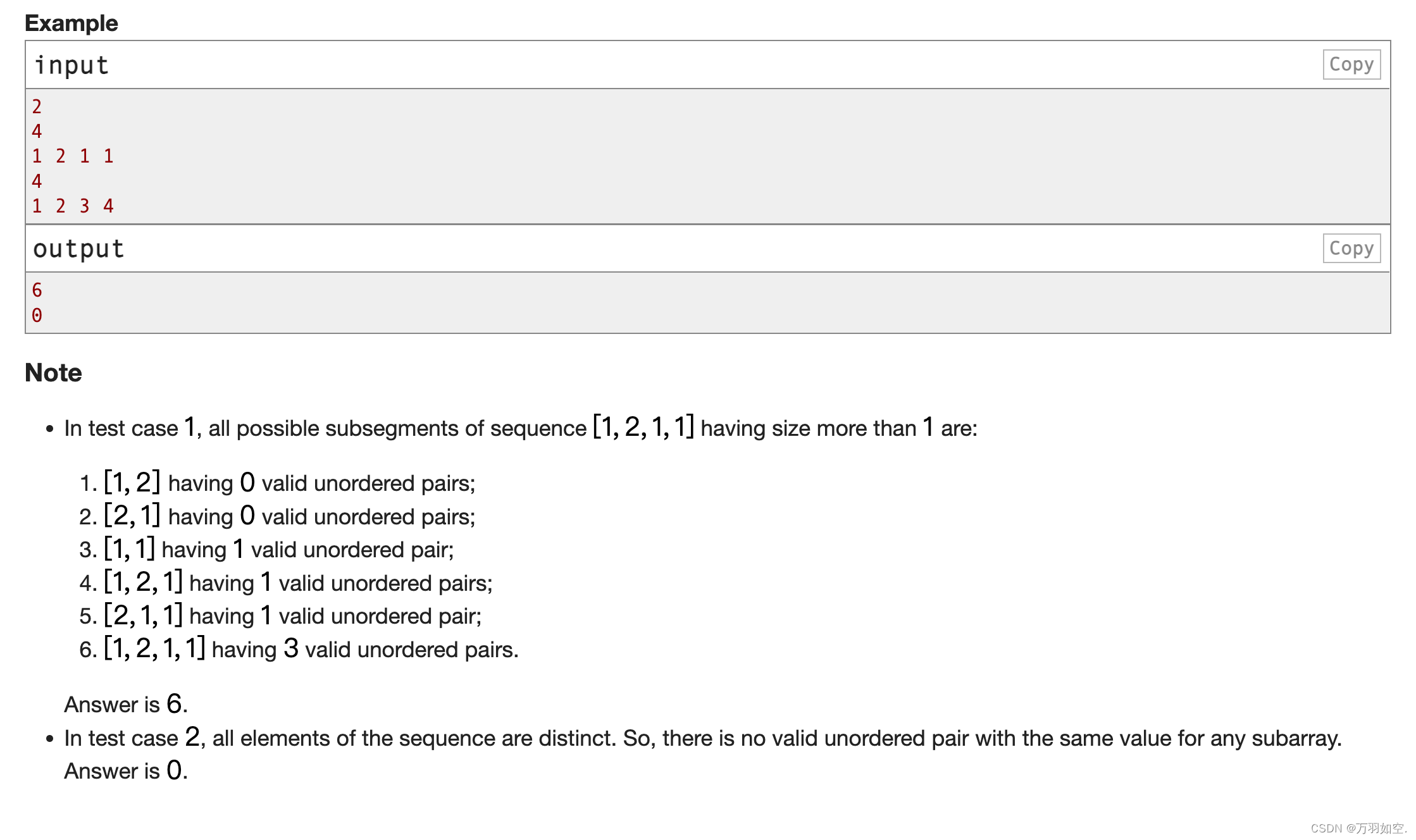
在测试用例1中，序列[1,2,1,1]的大小大于1的所有可能的子段为:
[1,2]有0个有效的无序对;
[2,1]有0个有效的无序对;
[1,1]具有1个有效的无序对;
[1,2,1]具有1个有效的无序对;
[2,1,1]具有1个有效的无序对;
[1,2,1,1]有3个有效的无序对。
答案是6。
在测试用例2中，序列的所有元素都是不同的。因此，对于任何子数组，都没有具有相同值的有效无序对。答案是0。

思路：所有子段可能，因为有有效的的无序对，对答案才有贡献。然后是所以子段和，我们可以分别对两边进行扩展，这样就是左右两边相乘，累加，就可以得出答案。

代码：

#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include <stdio.h>
#include<vector>
#include<queue>
#include<map>
#include<set>
#include<tuple>
#include<numeric>
#include<stack>
using namespace::std;
typedef long long  ll;
int n,t;
inline __int128 read(){
    __int128 x = 0, f = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9'){
        if(ch == '-')
            f = -1;
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9'){
        x = x * 10 + ch - '0';
        ch = getchar();
    }
    return x * f;
}
inline void print(__int128 x){
    if(x < 0){
        putchar('-');
        x = -x;
    }
    if(x > 9)
        print(x / 10);
    putchar(x % 10 + '0');
}

ll w;
void solv(){
    map<ll,ll>q;
    cin>>n;
    ll ans=0;
    for (int i =1; i<=n; i++) {
        cin>>w;
        ans+=q[w]*(n-i+1);
        q[w]+=i;
    }
    printf("%lld\n",ans);
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(); cout.tie();
    cin>>t;
    while (t--) {
        solv();
    }
    return 0;
}