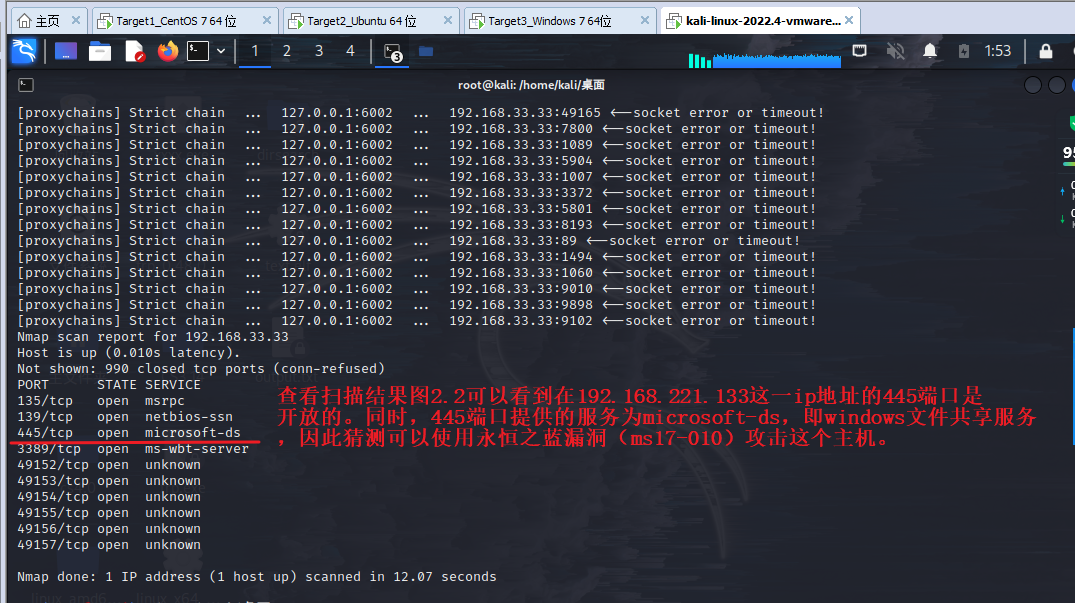
仍是上一节中提到的基本思想
武忠祥老师每日一题||定积分基础训练(一)

在这个题中,M和N可以利用奇偶性判断。
如下:

从上可知,
M
=
∫
−
π
2
π
2
1
d
x
M=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}1\,{\rm d}x
M=∫−2π2π1dx
而对于N,一个基本的不等式有:
1
+
x
≥
e
x
,
当且仅当
x
=
0
“
=
”成立
1+x\ge e^x,当且仅当x=0“=”成立
1+x≥ex,当且仅当x=0“=”成立
(这个可以利用函数单调性进行证明)
下为几何上的直接展示:

故
1
+
x
e
x
≤
1
(
当
x
=
0
时,“
=
”成立
)
故\frac{1+x}{e^x}\le 1(当x=0时,“=”成立)
故ex1+x≤1(当x=0时,“=”成立)
由于M,N积分区间相同,故可得M>N.
综上,K>M>N
武忠祥老师每日一题||定积分基础训练(二)
news2026/2/13 17:59:08
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/485009.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
The 1st Universal Cup Stage 13: Iberia, Apr 22-23, 2023 题解
D. XOR Determinant
You are given two arrays b and c of length n, consisting of non-negative integers. Construct n n matrix A as Aij bi ⊕ cj . Find the determinant of A modulo 998 244 353
考虑 A i j ∑ k b i , k c j , k p A_{ij}\sum_k b_{i,k}{c_{j,k}…
基于GWO灰狼优化算法的城市路径优化问题GWO-TSP(MATLAB程序)
资源地址:
基于GWO灰狼优化算法的城市路径优化问题GWO-TSP(MATLAB程序)资源-CSDN文库
主要内容:
主要采用灰狼优化算法对城市间的路径进行规划。城市分布图如图所示。 部分代码:
% 产生问题模型 model CreateModel(Oliver30.…
p70 内网安全-域横向内网漫游 Socks 代理隧道技术(NPS、FRP、CFS 三层内网漫游)
数据来源 本文仅用于信息安全学习,请遵守相关法律法规,严禁用于非法途径。若观众因此作出任何危害网络安全的行为,后果自负,与本人无关。 必要基础知识点:
内外网简单知识内网 1 和内网 2 通信问题正向反向协议通…
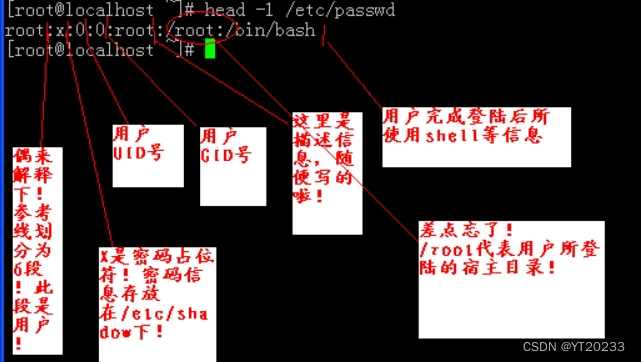
linux用户管理指令
这里写自定义目录标题 一 增加新用户及密码二 切换用户三 userdel 删除用户四 查看用户登录信息五 让普通用户成为管理员1. 修改环境配置文件2.设置用户和密码 六 查看创建哪些用户 一 增加新用户及密码
useradd:加用户名 passwd:加用户密码
[rootlocalhost ~]# u…
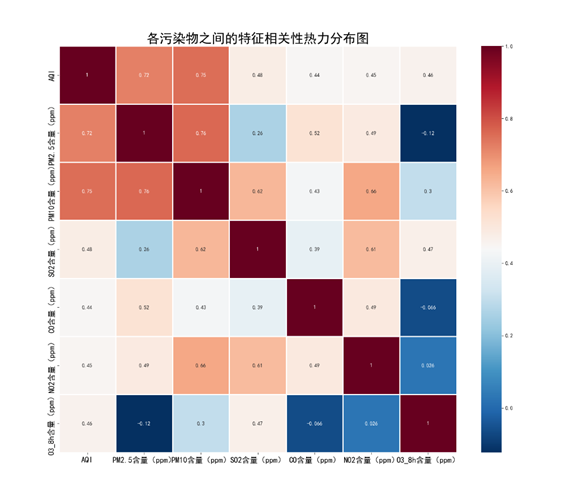
【Python】芜湖市空气质量指数可视化(散点图、分类散点图、单变量分布图、线性回归拟合图、相关性热力图)
【Python】芜湖市空气质量指数可视化 本文仅供学习参考,如有错误,还请指正! 一、简介
空气质量指数(Air Quality Index,AQI )简而言之就是能够对空气质量进行定量描述的数据。空气质量(Air Quality )的好坏…
《SQLi-Labs》02. Less 6~10
sqli Less-6知识点题解 Less-7题解 Less-8题解 Less-9知识点题解 Less-10题解 sqli。开启新坑。 Less-6
知识点
布尔盲注。与 Less-5 基本相同。这里只简略写大致步骤。
length() 函数:返回字符串所占的字节数。ascii() 函数:返回字符串最左字符的ASC…
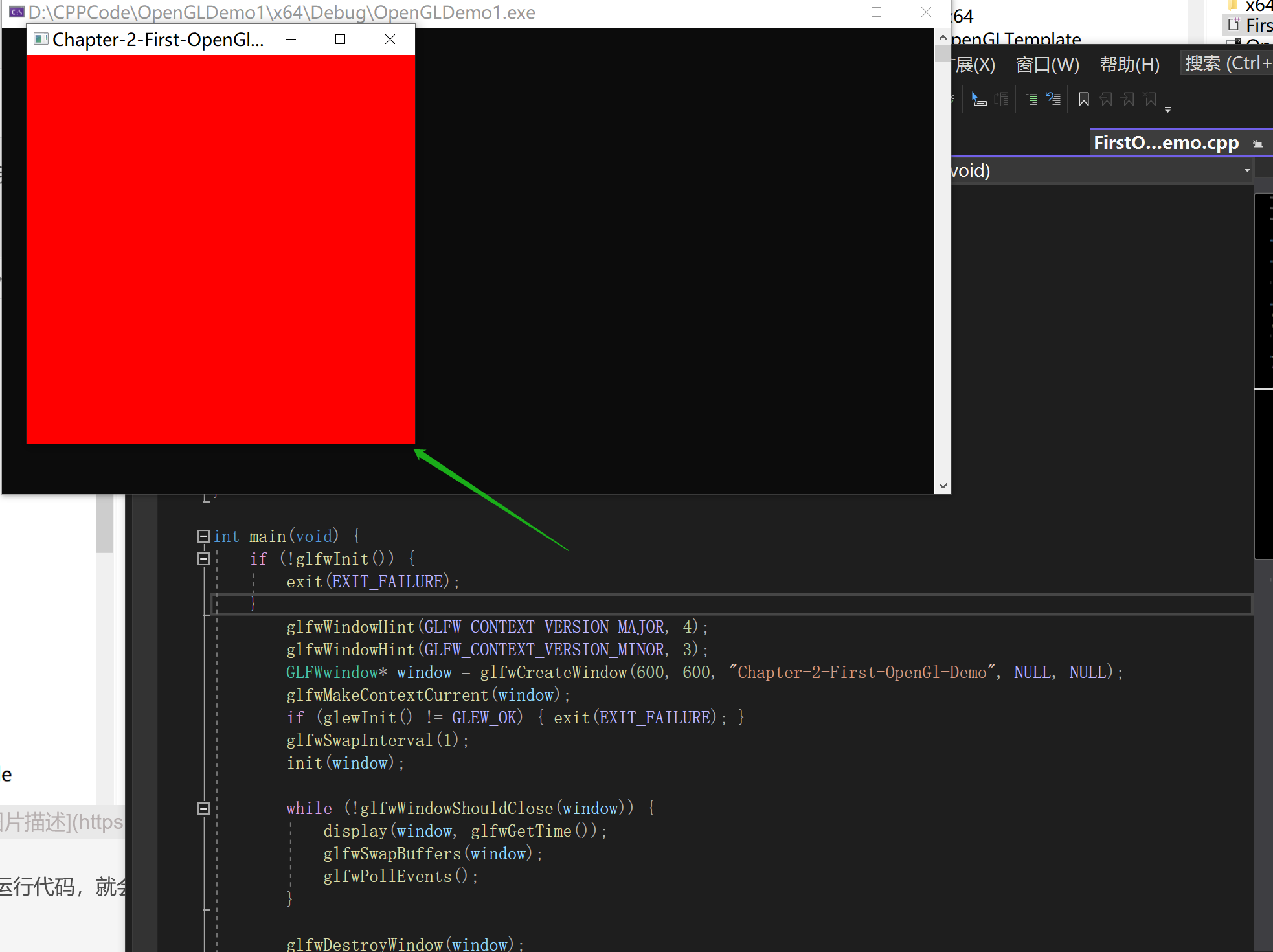
OpenGL开发必过的坎------开发环境的准备(Windows10)
前言
图形编程一直以来都是计算机科学中最具挑战性的主题之一。随着限制VR技术的兴起,越来越多的公司开始涉足VR领域。目前来看使用最多的是Unity3d来开发,但是像浏览器,将2D应用3D化(把2D的应用界面投到一个3D的场景中ÿ…
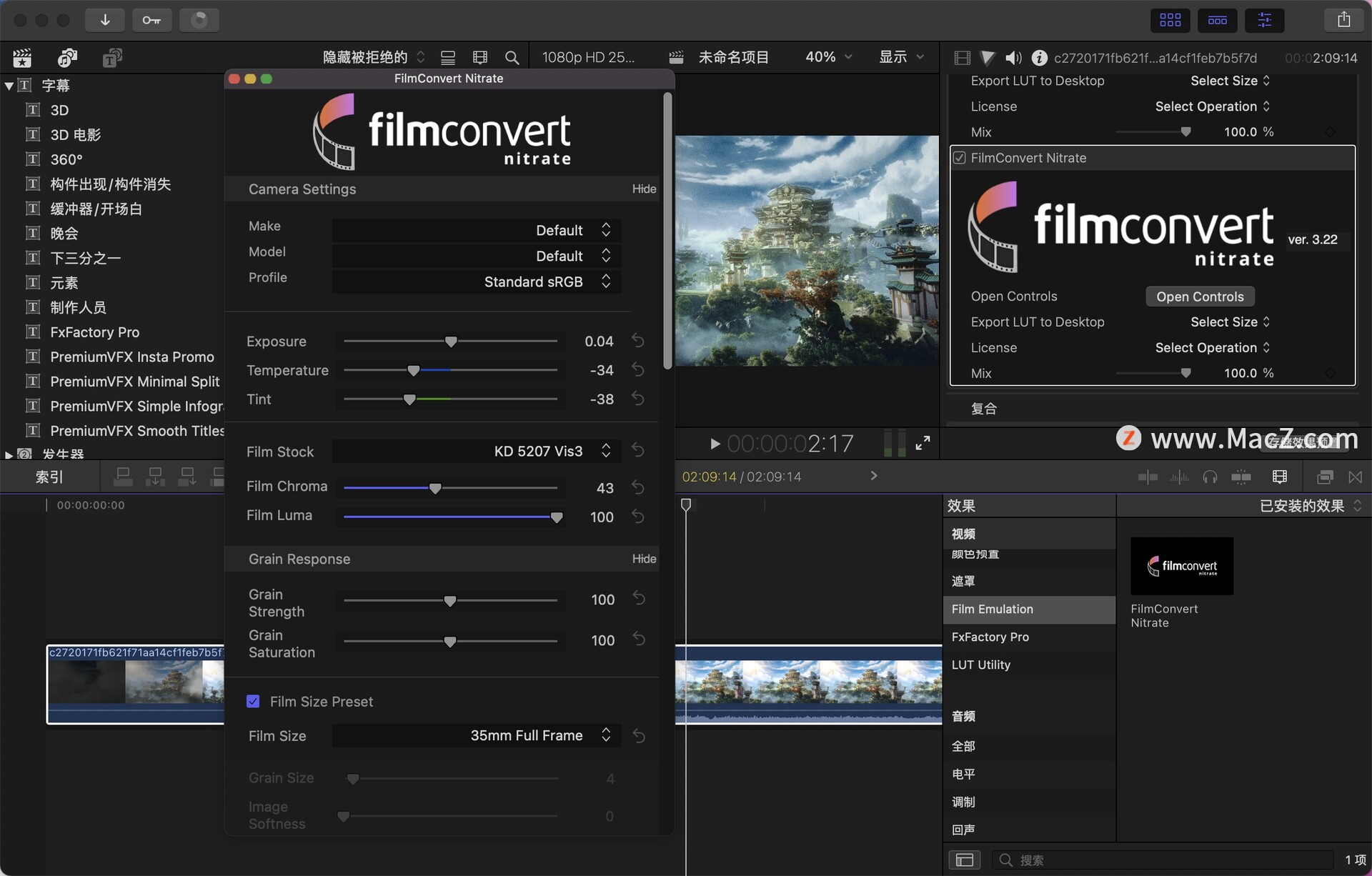
FilmConvert Nitrate for Mac(fcpx/胶片模拟调色Pr/AE插件)
FilmConvert Nitrate是一款针对视频后期处理的插件,可用于颜色校正和外观看调整。它提供了各种预设,以方便用户足够快速地修改视频的外观,并还包含一个自定义工具集,以方便用户可以调整多个参数来达到他们所需要的效果。
该插件支…
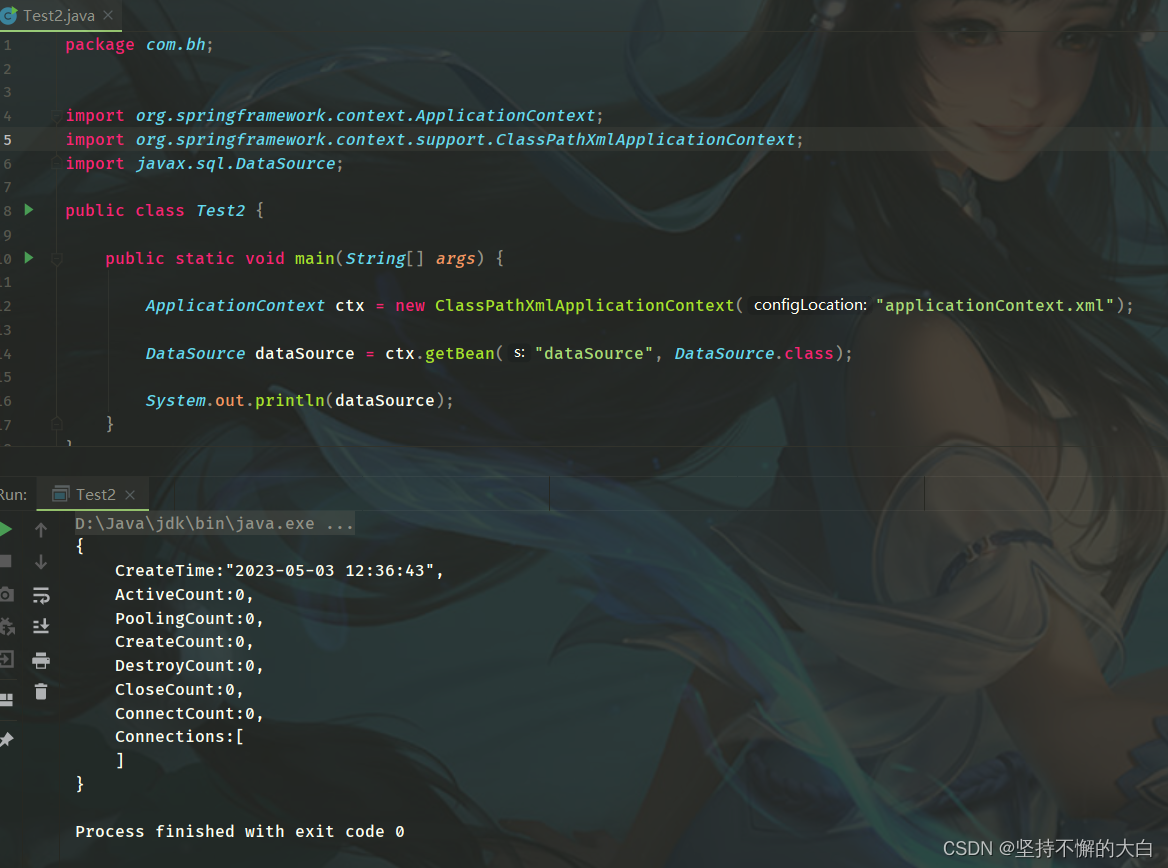
SpringBoot + Druid DataSource 实现监控 MySQL 性能
1 添加依赖
<properties><java.version>1.8</java.version><alibabaDruidStarter.version>1.2.11</alibabaDruidStarter.version>
</properties><dependency><groupId>com.alibaba</groupId><artifactId>druid-s…
Python基础合集 练习24 (程序调试)
assert expression[,arguments]
expression条件表达式语句,如果表达式的值为真,则程序会继续执行下去,如果值为假则程序抛出Assertionerror错误,并输出指定的参数内容
arguments可选参数
if not expression:
raise AssertionError(argument)
def num_ca(): book int(inpu…
Rust 一门赋予每个人构建可靠且高效软件能力的语言
目录
Rust
安装
尝试
hello, world
编译
链接出错
开启 Rust 之旅
官方教程
《Rust 程序设计语言》
《通过例子学 Rust》
核心文档
标准库
版本指南
CARGO 手册
RUSTDOC 手册
RUSTC 手册
编译错误索引表
非官方翻译教程
Rust 程序设计语言 简体中文版
通…
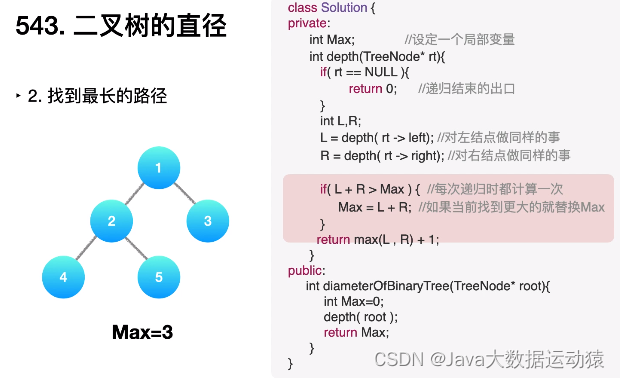
543. 二叉树的直径【71】
难度等级:容易 上一篇算法: 199. 二叉树的右视图【111】 力扣此题地址: 543. 二叉树的直径 - 力扣(Leetcode) 1.题目:543. 二叉树的直径
给定一棵二叉树,你需要计算它的直径长度。一棵二叉树的…
玩一玩 Ubuntu 下的 VSCode 编程
一:背景
1. 讲故事
今天是五一的最后一天,想着长期都在 Windows 平台上做开发,准备今天换到 Ubuntu 系统上体验下,主要是想学习下 AT&T 风格的汇编,这里 Visual Studio 肯定是装不了了,还得上 VSCode…
Spring:依赖注入的方式(setter注入、构造器注入、自动装配、集合注入)
依赖注入的方式有setter注入、构造器注入、自动装配、集合注入 首先,Maven项目pom.xml依赖包如下: pom.xml
<?xml version"1.0" encoding"UTF-8"?>
<project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:…
Servlet中转发和重定向的区别
什么是转发,重定向?
转发和重定向都是用于在服务器和浏览器之间进行页面跳转的方式。
转发是在服务器内部进行的,当一个Servlet接收到请求后,它可以将请求转发给另一个Servlet或JSP页面来处理请求,但是浏览器不知道这…
C语言-学习之路-04
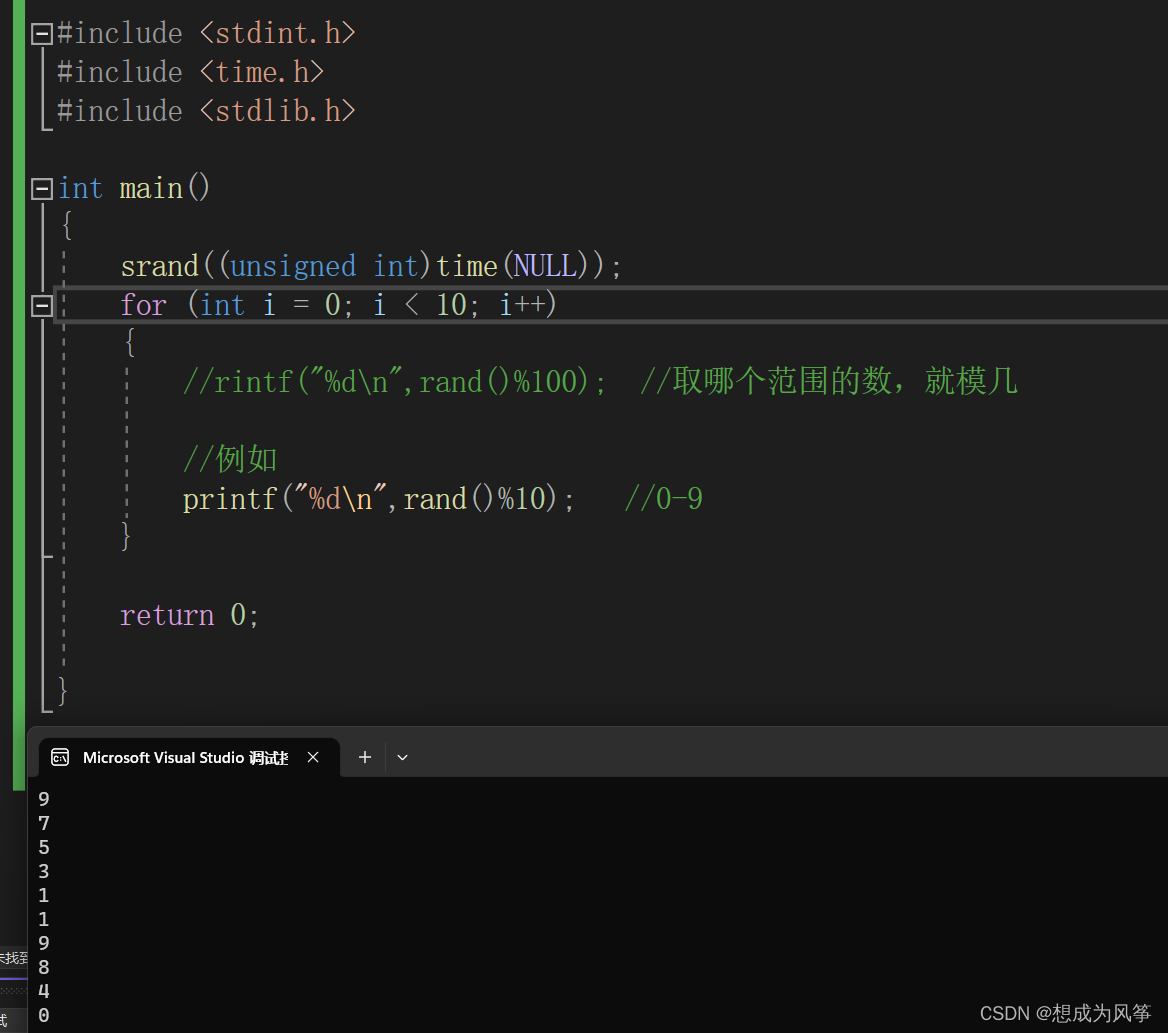
C语言-学习之路-04 数组与字符串一维数组一维数组的定义和使用一维数组的初始化数组名一维数组练习 二维数组二维数组的定义和使用二维数组的初始化数组名 字符数组与字符串字符串的输入输出随机数字符串处理函数 数组与字符串
数组:为了方便处理数据把具有相同类型…
等保工作的定级指南文件
定级主要依据国家标准信息安全技术网络安全等级保护基本要求来整改。有关等保工作流程和明细,请见:https://luozhonghua.blog.csdn.net/article/details/130465356?spm=1001.2014.3001.5502 5网络安全等级保护概述 5.1等级保护对象 等级保护对象是指网络安全等级保护工作中…
微服务注册中心-Nacos概述
1、Nacos基本介绍
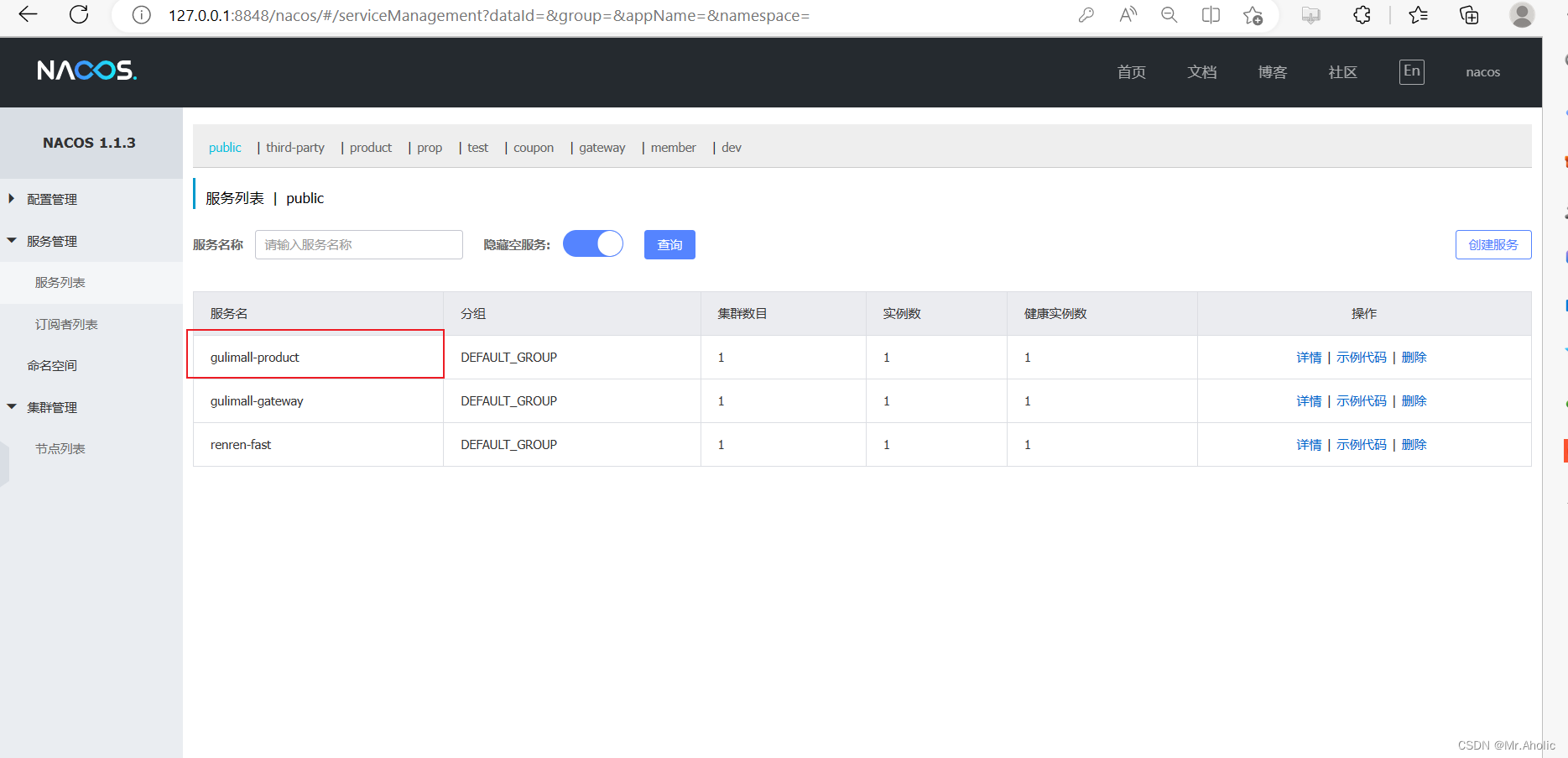
1.1. 什么是 Nacos?
Nacos 是阿里巴巴推出来的一个新开源项目,这是一个更易于构建云原生应用的动态服务发现、配置管理和服务管理平台。
Nacos 致力于帮助您发现、配置和管理微服务。Nacos 提供了一组简单易用的特性集,帮…
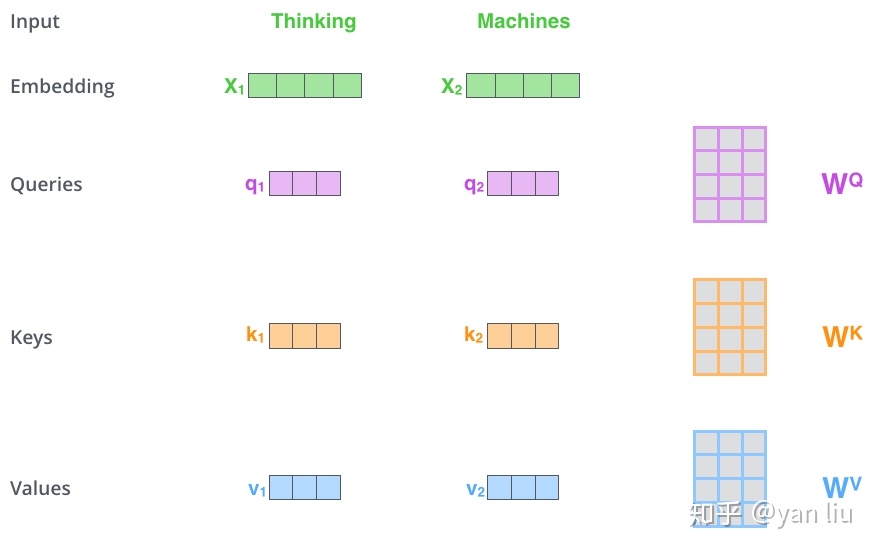
详解Transformer (Attention Is All You Need)
先导知识
Attention残差网络Layer Normalization
前言
注意力(Attention)机制[2]由Bengio团队与2014年提出并在近年广泛的应用在深度学习中的各个领域,例如在计算机视觉方向用于捕捉图像上的感受野,或者NLP中用于定位关键token…